『電気回路の配線 Part2』解答
◆東京都 鳥居 さんからの解答。
用語の定義として、3n個の点のうち凸多角形の頂点に来るものを外側、来ないものを内側と呼ぶことにする。
3n=3のときは明らかである。
3n≧6のときの解答の方針は、3n個の点を直線にて2つの組に分け、点の個数が少なくなる問題に帰着できることを示す。
(1) 内側に青い点がある場合
内側の青い点を通る直線を考え、その直線によって分けられる2つの領域をAとBとする。
fを「領域Aにある赤い点の個数×2−青い点の個数(ただし直線上の点は個数に数えない)」とする。
直線を回転させるとfの値は変化していく。
赤い点がA領域に入るごとにfは2だけ増える。
赤い点がA領域から出るごとにfは2だけ減る。
青い点がA領域に入るごとにfは1だけ減る。
青い点がA領域から出るごとにfは1だけ増える。
直線が半回転するとA領域とB領域が入れ替わる。
fの初期値をf0、半回転後のfの値をf1とすると、以下の式が成り立つ。
f0+f1=赤い点の全数×2−(青い点の全数−1)=1
f0≧1ならばf1≦0、f0≦0ならばf1≧1である。
どちらの場合においても、fの値は点の出入りによって±1,±2ずつしか変化しないため、半回転する間にfは0または1となる状態が必ずある。
f=0のときは回転の軸とした内側の青い点を領域Bに入れ、f=1のときはその青い点を領域Aに入れると、内側の点を通る直線による領域分割により領域A,Bにはどちらも点が必ず存在して、どちらも赤い点の個数×2=青い点の個数となる。
領域A,Bはどちらも問題にある点の個数の条件を満たしており、それぞれの領域の点の個数は領域分割前の点の個数から少なくなっている。
領域Aの中の点で3角形を作っていっても領域Aをはみ出すことはなく、領域Bでも同様なことがいえるため、領域A,Bそれぞれに作った三角形同士は重なることがない。
以上より、点の個数を少なくした問題に帰着できることが示せた。
(2) 内側に赤い点がある場合
外側の点に着目すると、赤い点の個数×2<青い点の個数となっている。
よって、外側の点で循環列を作ると、青い点が3個(以上)並ぶ箇所が必ず存在する。
その3個並んだ真中の青い点を通る直線を考え、(1)で定義した領域A,Bとfを導入する。
まず、領域Aはすべての点を含まないように初期状態を設定するとf0=0である。
直線の回転を始めると、隣の青い点が入ってきてf=−1となる。
半回転した状態ではf1=1であり、半回転に到達する手前で最後となる青い点が入ってくるため、その点が入ってくる前の状態ではf=2である。
よって半回転をする間に、初期状態と半回転状態以外にfが0または1となる状態があり、その状態では領域A,Bそれぞれ点が存在する。
(1)で示した方法に従い回転の軸となった青い点を領域A,Bいずれかに含めると、以下は(1)と同様な議論によって、(2)の場合も問題の帰着ができる。
(3) 内側に点がない場合
外側の点で循環列を作る。
赤い点1個と青い点が2個とが交互に来る場合、連続した3点の両端の点同士を結ぶ直線を考えると、その直線によって連続した3点とその他の点に領域を分けることができる。赤い点1個と青い点が2個とが交互に来ない場合は、青い点が3個(以上)並ぶところができるため、(2)と同様に議論を進めて問題の帰着ができる。
◆愛知県 Y.M.Ojisan さんからの解答。
【証明】
(1)n=1のとき可能であることは明らかである。
(2)今、n<m において可能であるとする。
n=m の時、下記の[補題1]により、平面上の点群を一本の無限直線により何れも空で無い左右2集合に分け、各々の集合において青点と赤点の数の比を2:1にすることが可能である。
また各集合のnは mより小さく、仮定によりそれぞれ重ならない三角形を作ることが可能である。
さらに、左右の点集合は直線で分断された点群であるので、作成された三角形が重なることはない。
よって、数学的帰納法により一般のnで可能である。

【補題1】
平面上の点の集合 R と B があって各々個数は
#R=n #B=2n である(nは自然数)。
また R+Bの如何なる3点も一直線上にはない。
このとき少なくとも1本の有向直線 L があって、
#(L[R>)=m #(L[B>)=2mとすることができる。
ここでmは1以上n未満の整数であり、L[A>は点の集合Aの点でLの右側にあるものの集合とする。
∵ R+Bの各点の有向直線Lへの垂線の足の並びをLの方位角に対して考える。
さらに最終的には数だけが問題なので、区別しないR側のn個の点列の間に、
B側2n個の点がどのように埋まりかつ移動してゆくかを考える。
このとき如何なる3点も同一直線上にはないので、ある方位角において3点以上の足が同一位置にあることはない。
従って R側の2点が交差しているところにB側の点の足があることもなく、R側の足の軌跡を単なるn本平行線としても殆どいたるところで一般性を失わない。
軌跡の例を図1に示す。
図1では0〜180度のみを示している。
180〜360度は上下反転したグラフである。
なぜならA度のLとA+180度のLは方向が逆なだけであるからである。
この性質は証明上重要である。
図1
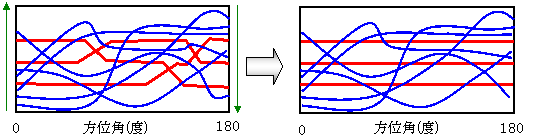
Rの点の値を:−2 Bの点の値を:1としてL方向に積算したグラフを考えると図2に示す4タイプに分類できます。(n=4)
0度において交差しないタイプaであるとき、180度位置では交差しないbタイプとなります。
従って、0〜180度の間に必ず交差するcタイプかdタイプが存在します。
これは少なくとも補題1を成立させるか、図2のcタイプに示したctypeの特殊ケースとして1だけずれている程度である位置があることを示しています。
この特殊なケースの場合は少なくともRの点が3個連続している必要があり、かつその両側にはBの点が最低1個存在しています。
ある方位とその方位+180度の方位の間では、その外側のBの点で最も端の点は、Rの点が3個連続しているところを通過しなければなりません。
このとき、Rは3点連続しているため、Rの隣接2点間に同時に入れるBの点は1個だけです。
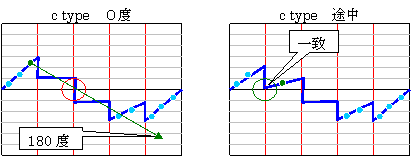
すなわちcタイプに示した特殊な状態も方位角を少し振れば、0値が存在します。図3参照
従って、 #(L[R>)=m #(L[B>)=2mとなるLが少なくとも1本存在します。
図2

図3
『電気回路の配線 Part2』へ
数学の部屋へもどる



