『電気回路の配線』解答

◆静岡県　ヨッシー　さんからの解答。

４０個の＋−の端子は、そのうちのいくつかの点を結んで出来る凸多角形の頂点または内部に存在する。

その頂点となる端子が、

  1. すべて＋、またはすべて−であるとき、例えばすべて＋とすると、
    頂点の＋端子１つと、内部の−端子１つを結ぶ直線を作ると、そのうちの少なくとも１つは、その直線によって、＋端子、−端子を同数ずつの２つのグループに分けられる。

    (理由）
    頂点の＋端子から出る半直線を右隣の頂点の端子から、左隣の頂点の端子まで、すべての端子を通りながら回転させ、
    ＋端子を通れば（１，０）、
    −端子を通れば、（０，１）を加えていくと、（＋、−）の値は、
    （１，０）・・・・・・・（１８，２０）（１９，２０）のように変化する。

    （１，０）では、＋が１つ多く、（１８，２０）では−が２つ多いので、
    この間に（ｘ，ｘ）（ｘ，ｘ＋１）となる、−端子が少なくとも１つあるはずである。
    その２つの端子を結ぶ。

  2. 頂点の端子に＋と−があるとき

    隣り合う＋端子と−端子を結び、残った端子を１つのグループとする。

以上の操作によって、４０個よりも少ない、＋−端子を同数含んだグループを作ることが出来る。
そのグループについて、同様の操作を繰り返せば、＋と−の端子が両端になるような２０本の線分が引けて、しかもどの２本も交差しないような結び方が出来る。

本当は、外周の点でなくても、良いのですが、説明しにくかったので、こうしました。
かなり、くどかったか？

【コメント】

　なるほど、一つの方法ですね。
もう少しじっくりと検討してみます。
証明からわかるように、４０個という数には無関係に、必ずショートしないように結ぶことが可能です。

◆東京都　eiki　さんからの解答。

うまく説明できないのですが。。。どこか勘違いしているかなぁ。。。
プリント配線の線幅に制限がないなら、すなわち純粋に理論的な問題なら証明もなにもあったもんじゃなく「自明」という気がするのですが。。。
だって（数学的でない接続詞ですね）どの配線も平面の絶縁盤上を２つに区切るわけじゃないから、他の配線を遮ることはできないでしょ？
だから何も考えなくてもひたすら交差しないように接続することは可能ですよね。
きちんと勉強したわけじゃないので突っ込まれると自信がありませんが、『トポロジー的に明らか』というのではダメでしょうか？
（＋−がそれぞれ１つ以上絶縁盤の周にあるなら話は全然変わりますが）

【コメント】

明らかといわれると、そうかなぁという気もしないではないのですが、線分で結ぶわけですから、明らかというわけにはいかないと思います。
たぶん。。。
ついでに言うと、絶縁盤の周上にあっても差し支えありません。

◆広島県　清川　育男　さんからの解答。

図がうまく書けないのですが。
「。」が端子の位置。
プラスの端子とマイナスの端子が同数個あるとする。

  　　
  図１−−−−−−−−−−−−−−−−
  　　　　A(+)。−−
  　　　　　　　　 　　　　B(-)。−−
  　C(+)。−−−−−D(+)。
  　　　　E(+)。−−
  　　　　　 F(-)。−−
  　　　　　　　　　G(-)。−−
  　　H(-)。−−
条件を満たすよう適当な位置に上記のように端子があるとする。
−−−−−−−に平行に下方にさがって行き上方にある端子から順番に書き上げていく。
同じ高さに２個ある場合は左を先に書く。
上記の場合は、A(+),B(-),C(+),D(+),E(+),F(-),G(-),H(-)。
左から順に相手をさがして結んでいく。
その結果は下記のようになる。
A(+)-B(-),C(+)-F(-),D(+)-G(+),E(+)-H(-)．．．．．（答え）

この方法でショートさせることなく配線出来ると思います。
ただし規準となる−−−−−−−はすべての端子より上方に決める。（その逆でも可）

　 「ただしどの３点も同一線上にない」というのがかなりきつい条件ですね。
実際に端子の位置を決めようとするときに。

◆東京都　eiki　さんからの解答。

いやはや、またまたやってしまいました、
得意の早トチリ。線分ですよね、線分。
となるとやはり『自明』ではないですね。
では、もう少し証明っぽくして。。。

接続すべき端子のペア数をＮとする。

  1. Ｎ＝１のとき
    　題意を満たすことは明らか（これは自明だ！よかった）

  2. Ｎ＝２のとき
    　接続の仕方は２通りあり、最悪でも１通りは題意を満たします。
    　（これは自明だと思うんですが、証明しろといわれると悩むなぁ）
    　すなわち交点はたかだか１個で、接続替え操作をするとその交点は解消します。

  3. Ｎ＝Ｋ（≧２）のとき、すなわち交点がたかだかＫ−１個のとき、題意をみたす接続方法があると仮定すると
  4. Ｎ＝Ｋ＋１のとき
    交点はたかだかＫ個で、そのうちの１個に着目すると、Ｎ＝２のときと同様、接続替え操作によってその交点を解消することができます。
    この接続替え操作によって、２本の線分がそれぞれ新たに別の線分と交差することがありますが、その交点はそれぞれたかだかＫ−１個だから、３の仮定によって題意をみたす接続方法があることになります。
以上、１，２，３，４より、すべての自然数Ｎについて、題意を満たす接続方法がある、といえます。
今度は”遅トチリ”かなぁ。

◆群馬県　数学好き３　さんからの解答。

＋の端子と−の端子の結び方は、２０！通りあります。
その中で２０本の線分の長さの和が一番短くなるような結び方（１とする）を考えます。
（結び方の数は有限ですから、これは必ず存在します。）

実は結び方１が求める方法（つまり交差していない結ぶ方）になります。

（証明）

背理法を用います。

結び方１の線分の中に交差する場合があると仮定します。

わかりやすくするため、結び方１の中の、
＋端子　Ｐ1と−端子　Ｍ1、
＋端子　Ｐ2と−端子　Ｍ2が図のように点Ａで交差しているとします。

この結び方をＰ1とＭ2、Ｐ2とＭ1を結ぶようにつなぎ変えます。
（他の線分の結び方は変えません）

Ｐ1Ｍ1＋Ｐ2Ｍ2
＝Ｐ1Ａ＋ＡＭ1＋Ｐ2Ａ＋ＡＭ2
＝Ｐ1Ａ＋ＡＭ2＋Ｐ2Ａ＋ＡＭ1

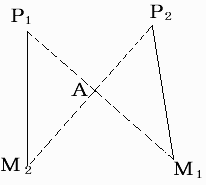
ここで三角不等式を用いると、 

上式＞Ｐ1Ｍ2＋Ｐ2Ｍ1

つまり
Ｐ1Ｍ1＋Ｐ2Ｍ2＞Ｐ1Ｍ2＋Ｐ2Ｍ1
したがって新しい結び方は、結び方１よりも線分の長さの和が短くなります。
これは結び方１の定義に矛盾します。

従って背理法により、交差する線分は存在しないことになります。

　『電気回路の配線』へ

　数学の部屋へもどる