◆広島県 清川 育男さんからの解答。
今回は3進法というか3に関係した問題ですね。
定規の長さを効率よく使って最大何cmまで測れるかと条件をつけると、規則性がはっきりするのではないでしょうか。
(個別には色々なやり方がありますが。)
| 目盛 | 目盛の入れ方 | 測れる長さ | 定規の長さ | 無駄 |
| 2個 | 1,3,2 | 6cm | 6cm | 0cm |
| 3 | 3,1,5,2 | 9 | 11 | 2 |
| 4 | 1,3,1,5,2 | 12 | 12 | 0 |
| 5 | 3,1,5,1,5,2 | 15 | 17 | 2 |
| 6 | 1,3,1,5,1,5,2 | 18 | 18 | 0 |
| 7 | 3,1,5,1,5,1,5,2 | 21 | 23 | 2 |
| 8 | 1,3,1,5,1,5,1,5,2 | 24 | 24 | 0 |
| 9 | 3,1,5,1,5,1,5,1,5,2 | 27 | 29 | 2 |
| 10 | 1,3,1,5,1,5,1,5,1,5,2 | 30 | 30 | 0 |
上記のような規則性が予想されます。
最大で「目盛りの数×3。」まで測れると思われます。
綺麗な規則性があるので上記の関係は正しいと思います。
【コメント】
実は私はパソコンで解いたのですが、関係を発見できていません。
そう単純ではないようです。
目盛りの数が4〜10の場合は、もう少し長い長さまで測定可能です。
ただし私の持っている解も、最長だという保障はないので、記録を更新した方はどんどん解答を送ってください。
◆広島県 清川 育男さんからの解答。
間違っていました。
4,6,8,10の場合は5を6に置き換えても連続しますね。
とりあえず、下記のように訂正します。
| 目盛 | 目盛の入れ方 | 測れる長さ | 定規の長さ | 無駄 |
| 4 | 1,3,1,6,2 | 13 | 13 | 0 |
| 6 | 1,3,1,6,1,6,2 | 20 | 20 | 0 |
| 8 | 1,3,1,6,1,6,1,6,2 | 27 | 27 | 0 |
| 10 | 1,3,1,6,1,6,1,6,1,6,2 | 34 | 34 | 0 |
【コメント】
おそらく4個の場合はこれが最善です。
(他にも13cmになる解は存在しますが)
6,8,10個の場合は、更に優れた解が存在します。
◆広島県 清川 育男さんからの解答。
目盛りの数をNとする。最大の計測数をKとする。
| K≦ | N2+3N+2 ―――――――― 2 |
【コメント】
はい、間違いなくこの関係は成立します。
◆広島県 清川 育男さんからの解答。
【問題3】
目盛りが5箇所のとき 無駄
1)1,1,1,5,5,4 0
2)1,1,4,4,4,3 0
3)1,1,6,4,2,3 0
4)1,1,6,4,3,2 0
5)1,3,6,2,3,2 0
6)1,7,3,2,2,2 0
7)3,2,1,6,4,4 3
以上7通りの方法で17cmまで測れる。
・目盛りが6箇所のとき。
1,3,6,6,2,3,2
23cmまで測定可能です。
・目盛りが7箇所のとき。
1,1,1,5,5,5,5,4
27cmまで測定可能です。
・目盛りが8箇所のとき。
1,1,1,5,5,5,5,5,4
32cmまで測定可能です。
・目盛りが9箇所のとき。
1,1,1,5,5,5,5,5,5,4
37cmまで測定可能です。
・目盛りが10箇所のとき。
1,1,1,5,5,5,5,5,5,5,4
42cmまで測定可能です。
奇数、偶数は分けて考えた方が言いようです。
5を6に変えた方がよくなります。
プログラムを組んで再度挑戦します。
【コメント】
目盛りが5カ所、6カ所のときは、正しいと思います。
7カ所以上のときは、さらに優れた解があります。
ただ私も最善であるという証明は持っていないのですが・・・。
◆広島県 清川 育男さんからの解答。
今度こそは規則性を見つけたと思います。
3,6,9,13,17,23,29,36,43,50
(1)1,2
(2)1,3,2
(3)3,1,5,2
(4)1,3,1,6,2
(5)1,3,6,2,3,2
(6)1,3,6,6,2,3,2
(7)1,3,6,6,6,2,3,2
(8)保留
(9)保留
(10)保留
上記が予想されます。古いコンピュータが働いています。
【コメント】
今度はたぶん正解だと思います。
証明は大変でしょうが、解の系列だけは何とかして見つけたいですね。
◆広島県 清川 育男さんからの解答。
目盛りが8カ所の場合
36
1,2,3,7,7,7,4,4,1 無駄 0
目盛りが9カ所のとき
43
1,2,3,7,7,7,7,4,4,1 無駄 0
目盛りが10カ所のとき
50
1,2,3,7,7,7,7,7,4,4,1 無駄 0
以上です。
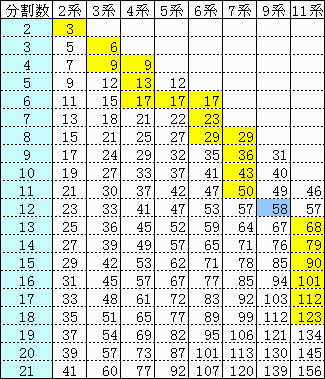
On-Line Encyclopedia of Integer Sequences(数列サイト)によると
3,6,9,13,17,23,29,36,43,50,
59,60,79,90,101,112,123,138
一般式は解っていないようです。
「minimal nodes in graceful graph with n edges」 とタイトルがついていました。
目盛りが11カ所のとき 59
目盛りが12カ所のとき 60 となっていますが、間違いではないのでしょうね。
1cmしか増加していないのが不思議な気もしますが、確認する元気はありません。
◆東京都 未菜実 さんからの解答。
以下 パズル数学入門 藤村幸三郎/田村三郎著
講談社・ブルーバックスp65〜,p282〜を参考にしました。
なお、表示の(*n)は括弧の前の数字がn個続くことを示します。
(1)2分割以上
1,2(*n) の形で 1 から 2*n+1 まで計れる。
(2)3分割以上
1,3(*n),2 の形で 1 から 3*n+3 まで計れる。
(3)4分割以上
1,1,4(*n),3 の形で 1 から 4*n+5 まで計れる。
(4)5分割以上
1,1,1,5(*n),4 の形で 1 から 5*n+7 まで計れる。
(5)6分割以上
1,3,6(*n),2,3,2 の形で 1 から 6*n+11 まで計れる。
(6)7分割以上
1,2,3,7(*n),4,4,1 の形で 1 から 7*n+15 まで計れる。
(7)9分割以上
1,1,4,2,9(*n),3,7,3,1
または
1,4,3,4,9(*n),5,1,2,2
で 1 から 9*n+22 まで計れる。
(11)12分割以上
1,1,3,5,5,11(*n),6,6,6,1,1 で 1 から 11*n+35 まで計れる。
上の中で最大計れるものが答えに該当します。
(すべてを網羅するわけではありませんが)
2分割:1,2
3分割:1,3,2
4分割:1,1,4,3
1,3,3,2
5分割:1,1,4,4,3
1,3,1,6,2
1,5,3,2,2
6分割:1,1,1,5,5,4
1,1,4,4,4,3
1,1,6,4,2,3
1,1,6,4,3,2
1,3,6,2,3,2
1,7,3,2,2,2
7分割:1,1,9,4,3,3,2
1,3,6,6,2,3,2
8分割:1,1,12,4,3,3,3,2
1,2,3,7,7,4,4,1
1,3,6,6,6,2,3,2
9分割:1,2,3,7,7,7,4,4,1
10分割:1,2,3,7,7,7,7,4,4,1
11分割:1,1,1,20,5,4,4,4,4,3,3
1,2,3,7,7,7,7,7,4,4,1
(以下は全部かどうか、最長かどうかも不明)
12分割:1,1,1,24,5,4,4,4,4,4,3,3
1,1,4,2,9,9,9,9,3,7,3,1
1,4,3,4,9,9,9,9,5,1,2,2
13分割:1,1,3,5,5,11,11,11,6,6,6,1,1
14分割:1,1,3,5,5,11,11,11,11,6,6,6,1,1
15分割:1,1,3,5,5,11,11,11,11,11,6,6,6,1,1
16分割:1,1,3,5,5,11,11,11,11,11,11,6,6,6,1,1
17分割:1,1,3,5,5,11,11,11,11,11,11,11,6,6,6,1,1
18分割:1,1,3,5,5,11,11,11,11,11,11,11,11,6,6,6,1,1
で、12分割は58、13分割は68になります。
なお、参考のためエクセルの表を添付しました。
参考にしてください。

◆富山県 N.C さんからの解答。
12分割の場合の最長が58か59かという問題ですが,
私も58を支持します。
1,1,1,24,5,4,4,4,4,4,3,3→58 1,1,4,2,9,9,9,9,3,7,3,1→58 1,1,6,7,1,10,10,10,3,4,2,3→58 1,2,3,11,7,3,11,7,4,4,4,1→58 1,2,3,11,3,7,8,10,4,4,4,1→58 1,4,3,4,9,9,9,9,5,1,2,2→582年ほど前に作ったプログラムをもう一度走らせてみた結果です。
◆富山県 N.C さんからの解答。
十進BASICで100行ほどのプログラムを作ってみました。
アルゴリズムは、両端から目盛りを刻んでいく単純なものです。
プログラムを1行でも短くするため、刻み込む目盛りの個数に両端を勘定に入れましたのでご注意を。
(8分割するときは1を足して,"9"と入力する)
●青木注
プログラムは Copy & Paste してお使いください。
REM 『定規のパズル』:「目盛り節約」物差し
REM N : 刻み込む目盛りの個数。(両端も数に入れる)
REM M : 現在、調べている物差しの長さ
REM K() : 刻み込んだ目盛りの位置を保管する配列
REM L() : 現時点で,長さxを計る方法がL(x)通りある。
input prompt "刻み込む目盛りの個数(両端を含む)は":N
dim K(N),L(N*(N-1)/2)
let K(1)=0
let K(3)=1
let L(1)=1
for M=N*(N-1)/2 to N step -1
print "check";M
let K(2)=M
let L(M)=1
let L(M-1)=1
let f=step1(N,K,L,M,3,N*(N-1)/2,1,0)
if f>0 then exit for
let L(M)=0
let L(M-1)=0
next M
print "最大長は";M
end
external function step1(N,K(),L(),M,i0,R,kr0,kf0)
REM 次に刻み込む目盛りの位置を調べる。
REM i0 : 現在までに刻み込んでしまった目盛りの個数
REM R : external function step2()を参照
REM kr0,kf0 : 前回に刻み込んだ目盛りの位置。
REM kf0=0のとき、左端から距離kr0の位置に
REM kf0=1のとき、右端から距離kr0の位置に刻み込まれる。
if i0<N then
let f=0
let kr=kr0
do while L(M-kr)>0
let kr=kr+1
loop
let kr=min(kr,ceil((M-(N-i0-1))/2))
do while kr>kr0
let f=f+step2(N,K,L,M,i0+1,R,kr,1)
let f=f+step2(N,K,L,M,i0+1,R,kr,0)
LET kr=kr-1
loop
if kf0=0 then
let f=f+step2(N,K,L,M,i0+1,R,kr0,1)
end if
else
let f=1
call printout(N,K)
end if
let step1=f
end function
external function step2(N,K(),L(),M,i,R,kr,kf)
REM 次の(i番目の)目盛りを刻み込む。
REM R : N個の目盛りがあれば,最大、N*(N-1)/2通りの計り方がある。
REM しかし、同じ長さを計る方法が複数あればそれは無駄になる。
REM R は、N*(N-1)/2から無駄になったペアの個数を引いたもの。
REM kr,kf : 今回、刻み込む目盛りの位置。
REM kf=0のとき、左端から距離krの位置に
REM kf=1のとき、右端から距離krの位置に刻み込まれる。
if kf=0 then
let ka=kr
else
let ka=M-kr
end if
let K(i)=ka
for j=1 to i-1
let len=abs(ka-K(j))
if L(len)>0 then let R=R-1
let L(len)=L(len)+1
next j
if R>=M then let f=step1(N,K,L,M,i,R,kr,kf)
for j=1 to i-1
let len=abs(ka-K(j))
let L(len)=L(len)-1
next j
let step2=f
end function
external sub printout(N,K())
REM 刻み込まれた目盛りの間隔を表示するルーチン。
dim a(N)
let a(1)=K(1)
let a(N)=K(2)
for i=3 to N
let j=i-1
do while K(i)<a(j-1)
let a(j)=a(j-1)
let j=j-1
loop
let a(j)=k(i)
next i
for i=1 to N-1
print a(i+1)-a(i);",";
next i
print "合計";a(N)
end sub