◆兵庫県 easylover さんからの解答。
【問題1】
0<r≦R …(1)
任意の円が内接するケースを考える。
d=R-r
d・πr2=π(R-r)r2
これをf(r)とおいて、f’(r)をとり増減を調べると、
| (1)の範囲内で、r= | 2 3 |
R のとき極大となる。 |
| このとき、d= | R 3 |
で、最大値は、 | 4 27 |
πR3 |
【問題2】
内接する三角形の面積をSとおいて、rが最大となるケースを考えようとしたのですが、
そしたら、d=0となってしまうようで行き詰まってしまいました。
指針が立ちません。
◆神奈川県 たこ焼き好き さんからの解答。
【問題2】
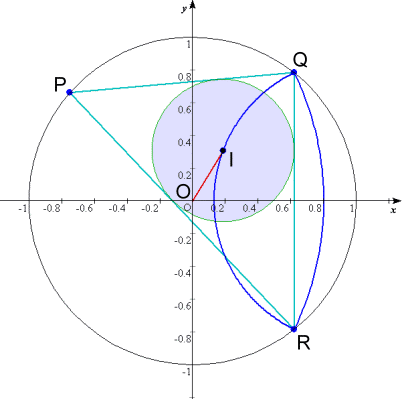
Oを基準にした位置ベクトルP,Q,Rを次のようにとる
P(cosφ,sinφ)
Q(cosθ,sinθ)
R(cosθ,-sinθ)

QR=p,PR=q,PQ=rとすると、
| △PQRの内心Iは、 | pP+qQ+rR p+q+r |
よって、
d(=OI)
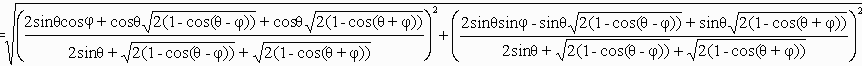
また、△PQR(面積S)の内接円の半径rは
| r= | 2S p+q+r |
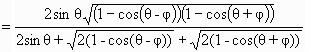
これより、f(θ,φ)=d・πr2といったθとφの二変数関数の問題に帰着・・・
といったところで、計算に挫折しました。
もっとイイやり方がありそうですね。
後はこれの増減などを調べるんですが・・・
解答になってなくてすいません
◆北海道 小西 さんからの解答。
【問題2】
定理名は忘れてしまいましたが、最近掲示板で以下の定理を目にしました。
|
楕円に凸n角形が外接しており、さらにそのn角形に楕円が外接しているとき、 外接楕円上の任意の点を頂点の一つとする同様のn角形が存在する。 |
この定理を利用します。
外接円の中心をO、内接円の中心をIとし、OIの延長と外接円の交点のうちO側をAとする。
上記の定理よりAを頂点とし、円Oに内接し、円Iに外接する二等辺三角形ABCが存在する。
BCと内接円の接点をMとし、
BM = x、∠IBM = ∠ABI = θとおく。
△OBMについて三平方の定理より
x2 = R2 - (r + d)2 … (1)
| △IBMより、tanθ = | r x |
| △ABMより、tan2θ = | R + r + d x | … (2) |
tanの倍角公式より
| tan2θ = | 2tanθ 1 - (tanθ)2 | = | 2rx x2 - r2 | … (3) |
(1),(2),(3)よりθとxを消去して整理すると、
| r = | R2 - d2 2R |
よって、
| dπr2 = | dπ(R2 - d2)2 4R2 |
f(d) = d(R2 - d2)2 とおいてf’(d)の増減を調べる。
f’(d) = 5d4 - 6R2d2 + R4
| f’(d) = 0 を満たすのは d = ±R, d = ± | R |
d < 0は不適。
d = Rはdπr2 = 0となり不適。
| ゆえに、d = | R |
のときdπr2は最大値を取り、 |
| その値は | 4 125 |
πR3 |
rがRとdだけで決まるのが不思議ですね。
最初に書いた定理に頼らずに解きたかったんですが、なかなかうまくいきませんでした。
◆出題者のコメント
みなさん、解答ありがとうございます。
【問題1】は、easyloverさんが簡潔に示されたとおりです。
「2円は接する筈」とさえ判れば、難しい問題ではありません。
【問題2】ですが、たこ焼き好きさんの途中での挫折とても残念です。
それにしても、ものすごい計算力ですね。
三角関数が苦手な私にはとても真似は出きません。^^;
それから小西さん、みごと正解です。
【問題2】は、示された定理を知らなかったら誰でも間違いなく苦戦するでしょうね。
その定理から、R2−d2=2Rr の関係式が導ければ殆ど解けたようなものです。
例の掲示板ですが、実は定理を教えてもらったのがこの私で、教えてくれたのが「いわしさん」です。
とても面白い定理に思え、早速それを利用するような問題を作ってみました。
それが【問題2】です。
参考までに…。
円(中心O)が図で与えられるなら、それに内接する三角形の内接円の半径は、任意な中心位置(o')に対し一意に作図可能です。
(図では、O-o'を結ぶ中心線の他には、外接円の右下4分1にある1つの青い円弧と3つの青い線分しか作図には必要ありません。)
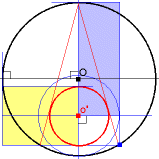
(図で、青い円と求める赤い円は同心円であり、
薄青色の長方形の面積(R2−d2)と
薄黄色の長方形の面積(2Rr)は等しい。)