◆愛知県 イマ イクゾウ さんからの解答。
この問題の「最少対局数」の意味がはっきりしません。
AがBに勝つ(AがBより強い)ことを A>B と表すことにします。
4人の場合で言います。
(1)
上位2人が A,B であるとして、そのことの証明をするという立場で言えば、
A>B,B>C,C>D
(AとBは入れ替わってもよく、CとDも入れ替わってもよい。以下同様)
はもちろんで、
Bを基準にして、AがBより強く、C,DがBより弱いことを示すか、
Cを基準にして、A,BがCより強く、DがCより弱いことを示すしかない。
すなわち A>B,B>C,B>D または A>C,B>C,C>D を示せばよい。
よって、必要対局数は 3 といえる。
一般に 2n人についての上位半数決定最少対局数は
明らかに、2n−1
(2)
誰が強いか弱いか分からないとき、一定の試行錯誤をしなければならない。
無駄な対局をできるだけ省く対局の手順を考えると
(2) のような意味での一般の場合の最少対局数は、簡単ではなさそうで、今は時間が足りません。
◆出題者のコメント。
ご指摘のとおり、「最少対局数」の意味が今一つ曖昧でした。
運が良く、1番少ない対局数で上位半数が決まる場合の最少対局数ではありません。
イマ イクゾウ さんの(2)に相当します。
混乱しないように、問題文の表現を一部改めました。
囲碁の対局の場合、引き分けはなく必ず勝敗の決着がつきます。
その上、囲碁の強さを絶対的としたため、大会参加者はそれぞれ異なる強さ(絶対量)を持つことになります。
そのように考えると、この問題は次の問題のようにもなります。
それぞれ重さの異なる2n個(n=2,3,4,5)の玉を、重い方の半分と軽い方の半分とに分けるために、天秤を何回使用しなければならないか、その回数を求めてください。
ただし、天秤は2つの玉の重さの比較だけに使うものとします。
◆愛知県 Y.M.Ojisan さんからの解答。
【解答】
参加者数を2N人とするとき N2回 の方法がある。
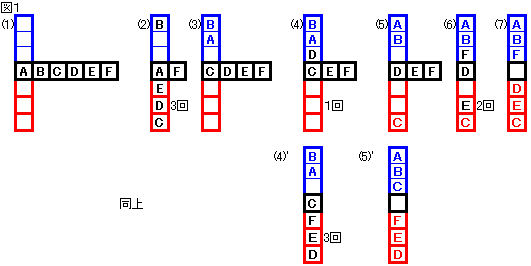
【方法】(図はN=3の場合で代表)
(1)
図1の(1)のように、参加者を一列に並べ(黒枠2N個)、上位者枠(青枠N個)、下位者枠(赤枠N個)を作る。
(2)
先頭の人(A)を「仮の中央値」とし、B以下との対戦を順次行い、Aより強い人を上位者枠に弱い人を下位者枠に詰めて行く。
するといつか図1の(2)のように、上位者枠または下位者枠が満員になるときが来る。
(3)
この時、満員になった枠と逆の枠内の人とAの計1人以上の参加者の位置が決定する。
図1の(3)ではA,Bが上位者に決定。
残りの位置未定の人を再度一列にならべ、先頭の人(C)を「仮の中央値」とし、残りの人(D以下)を順次対戦させる。
(4)
するとまたいつか図1の(4)ないし(4)’のように上位者枠または下位者枠が満杯になり、同様に少なくとも1人の位置が決定する。
図1の(5)’参照。
(5)
以上繰り返すことにより、上位者と下位者を分けることができる。
図1(5)〜(7)参照。

【この方法の最悪回数】
満杯になったときに位置が決まる人数が常に1人であるときが最悪である。
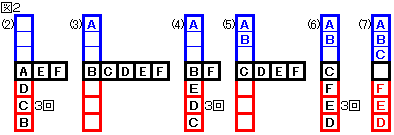
図2のように上位者ばかりが決まる場合は、
N人決定×満杯までN回勝負=N2回
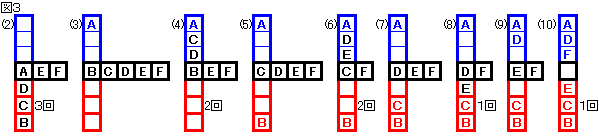
図3のように上位者と下位者が交互に決まる場合も、勝負数は同じく
N+2(N−1)+2(N−2)+・・・+2
=N+N×(N−1)
=N2回 である。
一般に上位者p人、下位者q人に分ける場合の
この方法の最悪回数をGo(p、q)とするとき、
Go(p,q)=pqが予想され、
この結果Go(N,N)=N2が得られると予想される。
この予想は正しく、証明を下記に示す。
ただし、p、q≧1。
【予想の証明】
Go(p,q)=p*qを漸化式で証明する。
(1)
Go(p,1)=Go(1,p)=p*1 である。
これは、優勝者またはドベを1人決めることであり、トーナメントの試合数の理論からも明らかである。
(2)
この方法によれば、Go(p,q)は I(≧q)回勝負後、下位が満杯の場合と
J(≧p)回勝負後、上位が満杯の場合の中で最大の回数である。
このとき、それぞれ 1+I−q人 、1+J−q人の参加者の位置がきまる。
一方、残された参加者間の優劣の情報は全く無いので、漸化式は下記である。
Go(p,q)
=Max{Max{I+Go(p-(1+I-q),q)},Max{J+Go(p,q-(1+J-p))}}
=Max{Max{I*(1-q)+(p-1+q)*q},Max{J*(1-p)+p*(q-1+p)}}
p、q≧1であるので、I=q、J=p の時が最大である。従って、
Go(p,q)
=Max{q+(p-1)*q,p+p*(q-1) }
=p*q
よって、予想式は正しい。
【P.S】
N2回が最小である方の証明はできませんでした。
◆出題者のコメント。
大会参加者の数を2N人とした時、N2回の対局数は確かに上位半数を決定するのに十分な対局数です。
でも、N=1やN=2の時以外は、必要最少限の対局数とはなりません。
N2回とすれば、6人(N=3)なら9回の対局になりますが、そうとも限らない反例を示します。
6人(N=3)なら8回でも済みます。
(最少とは別ですが・・)
6人を任意の3人ずつの2グループに分けます。
各々のグループ内の3人の強さの順番を決定するのに、最悪でも3回の対局で済みます。
(合計6対局)
すると、必ず下の図のようになります。
図の線で結ばれている者同士では、上にある者が下にある者より上位者です。
経路(上から下の1本線)が並列の時の、上位者同士や下位者同士の強弱は不明です。
○ ○ | | ◎ ◎ | | ○ ○そこで、上の図の◎同士で対局します。(7対局目)
○ | ○ ◎ |\| ◎ ○ | ○そこで、上の図の◎同士で対局します。(8対局目)
● ● | | ● ● ● | |X| ● ○ ○ | or | ○ ○ | ○ | ○(右の場合、すべての●はすべての○より上位になっています)
◆東京都 goya さんからの解答。
参加者数を 2N で表わします。
1人づつ選出し、その人と既に選出済みの人の数人と対戦していく。
誰とどの順番に対戦するかは選出された順番によりパターン分けされます。
以下では、n番目に選出された人を Bn と表わします。
◎前半の N人
まず、1番目は選出済みの人がいないため対戦はありません。
2番目の人は1番目と対戦する。
これでB1とB2の順位が確定。
○3〜N番目
Bnは既に確定している順位(n-1位まで)の中間の順位の人と対戦する。
(注)
B4はB1〜B3の中での順位2位の人と対戦
B5はB1〜B4の中での順位の中間が2.5位となるため2位と対戦
対戦の結果 Bn が勝者なら1つ上位と対戦。
それに勝てばもう1つ上位というように負けるか1位に勝つまで対戦していく。
対戦の結果が Bn の負けなら、これとは反対に1つ下位から最下位方向に勝つまで対戦していく。
※ 以上によってn人の中での1〜n位が確定する。
BNの対戦が終わると参加者数の半数である N人の順位付けができる。
◎後半の N人
○(N+1)〜(N + N/2)番目
Bnは確定している順位(N位まで)の中間の順位の人と対戦する。
※ N=5の場合、B6〜B8は 3位の人と対戦
対戦の結果 Bn が勝者なら1つ上位と対戦。
それに勝てばもう1つ上位というように負けるか1位に勝つまで対戦していく。
対戦の結果が Bn の負けなら、これとは反対に1つ下位から最下位方向にN位の人まで勝つまで対戦していく。
※ 以上によってn人の中での1〜N位が変動する。
N位以下は順位が不明。(分かるケースもあるが)
○(N + N/2)〜2N
Bnは (N-n)位の人と対戦する。
※ 最後に選出された人は N位、最後から2番目に選出された人は (N-1)位と対戦。
対戦の結果 Bn が勝者なら対戦は終わり。
対戦の結果が Bn の負けなら、1つ下位から最下位方向に N位の人まで勝つまで対戦していく。
【答え】
以上を対局数を求める式にすると次のようになります。
Nが偶数の時
| 対局数= | 5*N*(N+2)-8 8 |
Nが奇数の時
| 対局数= | 5*N2+8*N-5 8 |
よって、解答は次の通り。
| N | 参加者 | 対局数 |
| 2 | 4 | 4 |
| 3 | 6 | 8 |
| 4 | 8 | 14 |
| 5 | 10 | 20 |
| 6 | 12 | 29 |
| 7 | 14 | 37 |
【参考】
参加者数=4の場合の対戦手順を文章で書くと次のようになります。
1局目 B1対B2
2局目 B3対1局目の勝者
B3が勝ったら
3局目 B4対1局目の勝者
B4が勝者なら、B3とB4の2名が上位半数
B4が敗者なら、B3と1局目の勝者の2名が上位半数
B3が負けたら
3局目 B3対1局目の敗者
4局目 B4対3局目の勝者
B4が勝者なら、B4と1局目の勝者の2名が上位半数
B4が敗者なら、1局目の勝者と3局目の勝者の2名が上位半数
◆出題者のコメント。
goyaさんの解答について、Nが3以上の時は必要最少限の対局数とはなりません。
どのようにして、その一般解が導き出せたのか?
何故に、後半の N人を、
(N+1)〜(N + N/2)番目と(N + N/2)〜2N番目の2つのケースに分けて、対局順序に別な手法を採る必然があるのか?
以上の2点の理由が理解できません。
2N人の内のN人を全員順序付けするための対局数も、示された方法に従うと多過ぎます。
N=5の時を例にして、示された方法に従って対局数を求めてみます。
3人までは明らかに3対局必要です。
4人目のB4は、2位の人と対局して負ければ3位の人と対局しなければなりません。
ここまでで、合計対局数は5対局です。
5人目のB5は、2位の人と対局して負ければ3位の人と対局し、それも負ければ4位の人と対局しなければなりません。
ここまでで、合計対局数は8対局です。
ですから、示された方法に従うと、8対局になります。
しかし、実際には7対局で済みます。
よく知られている問題ですが、一般に、N個のもののソーティング(順序付け)のための必要最少限の比較回数は
log2(N!) ≦ kを満たす最小の整数kです。(証明省略)
ですから、N=5の場合は
log25!=log2120≒6.907
それ故、k=7 が可能な最小値になります。
他にも方法があるでしょうが、N=5の時の1つの例を以下に示します。
下の図で◎同士が対局し、●は全員の順序付け決定状態です。
線で結ばれている者同士では、上にある方が上位者で下にある方が下位者です。
初期状態 ◎ ◎ ○ ○ ○ 1対局後 ○ │ ◎ ◎ ○ ○ 2対局後 ◎ ◎ │ │ ○ ○ ○ 3対局後 ○ / \ ○ ◎ ◎ \ ○ ┌───────┴───────┐ 4対局後 ◎ ◎ ○ / \ / / \ ○ ○ ○ ○ \ / \ ○ ◎ ◎ ↓ └─────┬─────┘ 5対局後 ○ ○ │ / \ ○ ◎ ○ / \ \ ◎ ◎ ◎ \ \ ○ ○ ↓ └─────┬─────┘ ↓ ┌─────┴─────┐ 6対局後 ● ○ ○ │ │ / \ ● ○ ◎ ◎ │ │ \ / ● ○ ○ │ / \ │ ● ◎ ◎ ○ │ ● └─────┬─────┘ 7対局後 ● │ ● │ ● │ ● │ ●
◆愛知県 Y.M.Ojisan さんからの解答。
最少性証明・一般性の無い解ですが。
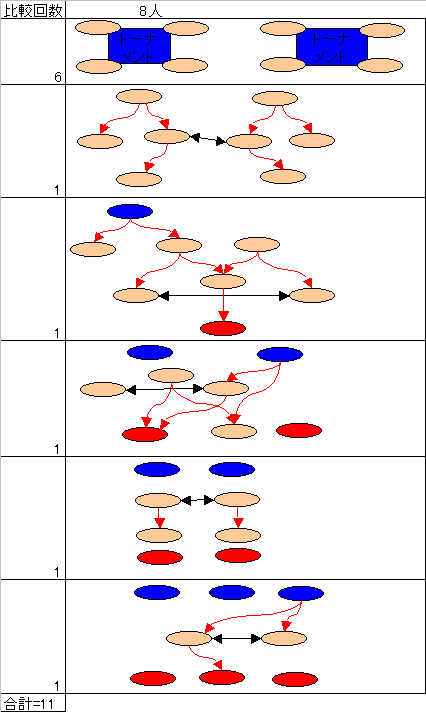
【問題 4人】 4回
楕円は参加者 黒矢印は対戦 赤矢印は優劣 赤楕円は下位決定 青楕円は上位決定
三角はトーナメントで2回対戦
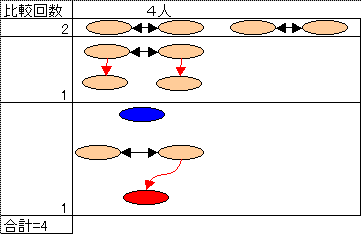
【問題 6人】 7回
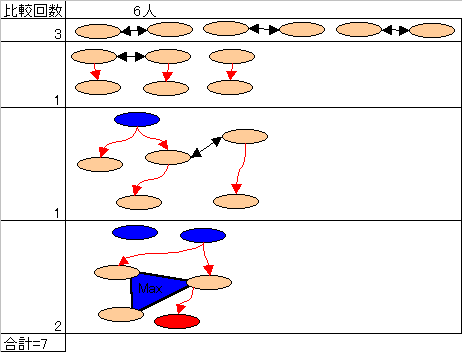
【問題 8人】 11回
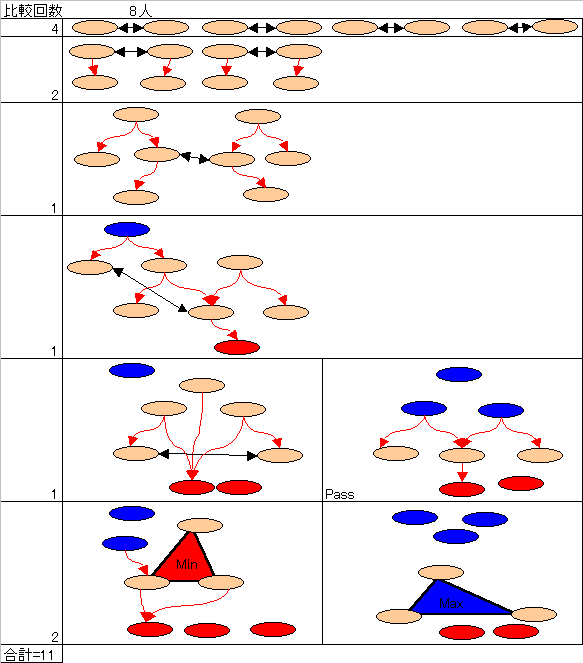
【問題 10人】 15回
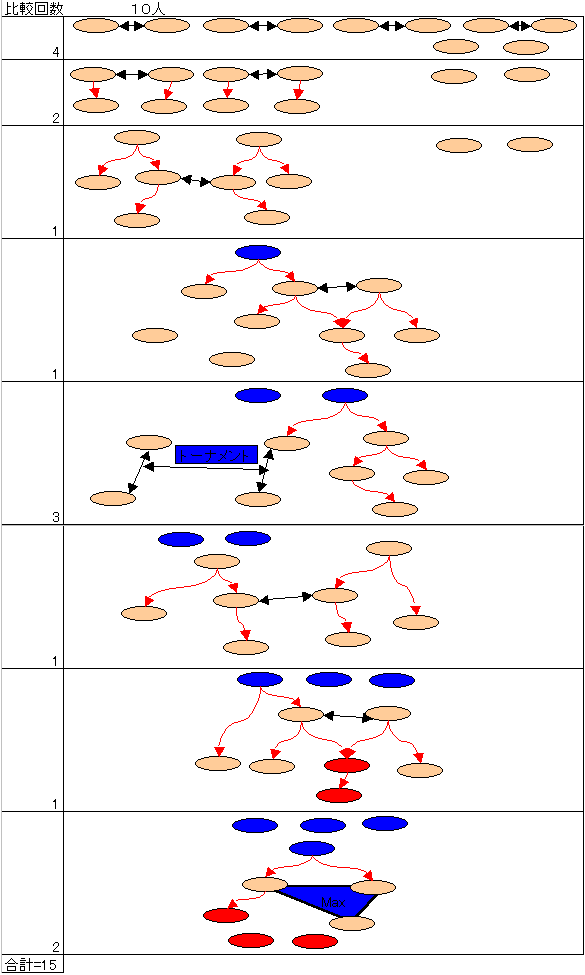
【P.S.】
試行錯誤解ですが、結果は規則性があるみたいです。
実験式は
| [ | N(N+8) 4 | ]−1 |
◆宮城県 アンパンマン さんからの解答。
O(n log n) でできる方法です。(最小ではありません。)
●nが偶数の場合:
n人を選んで強さを比較して順序付けします。
(Aグループとします。残りはBグループとします。)
Bグループから2人ずつを選んでAグループの人と比較しながらAグループに追加します。
例:
1 5 6 2 7 8 4 3
1)Aグループ: 1 5 6 2
順序付けすると 1 2 5 6 に変わります。
(4人の場合5回の比較が必要)
2)Bグループから 7 8 を追加します。
最初は7をAグループの人と比較します。
(Binary Searchによる比較を用いて比較する)
Aグループは 1 2 5 6 7 に変わります。
次は8を1 2 5 6 の人と比較します。
Aグループは 1 2 5 6 7 8に変わります。
(そのとき 7 8の順番がわかりません。)
3)Bグループから 4 3 を追加します。
4 3 を 5 6 と比較します。
(3回でできる)
そのときAグループは 3 4 1 2 5 6 7 8に変わります。
(そのとき 1 2 3 4の順番がわかりません。)
以上強い人は5 6 7 8であることがわかります。
●nが奇数の場合:
n人を選んで強さを比較して順序付けします。
(Aグループとします。残りはBグループとします。)
Bグループから2人ずつを選んでAグループの人と比較しながらAグループに追加します。
最後に Bグループが一人残りますので、そのとき、Aグループの真ん中の人と一回比較すれば上位半数が決定できます。
上記の方法より、N(2n)は2n人がいるときの比較数と定義すると
N(2n)=T(n)+S(n;n), nが偶数の場合。
N(2n)=T(n)+S(n-1;n)+1、 nが奇数の場合。
T(n)はn人を選んで強さを比較して順序付きする比較数
(最良の最悪の場合を考える)。
S(r;s)はBグループ(r人)から2人ずつを選んでAグループ(s人)に追加するときの必要な比較数
(できるだけ最良の最悪の場合を考える)。
では、T(n)を計算します。
Binary Searchを用いるInsertion Sortを使うと、最悪の場合でもかなり少ない比較数で順序付けできます。
nが 2r≦n=2r+s<2r+1とすると,必要な比較数は
T(n)
| = | n-1 Σ i=1 | ([log2i]+1) |
| =n-1+sr+ | 2r-1 Σ i=1 | ([log2i]) |
| =n-1+sr+ | r-1 Σ j=1 | j・2j |
| =n-1+sr+(r-2)2r+2 |
nが偶数の場合、S(n;n)を計算します。
2m≦n=2m+2k<2m+1とすると,Binary Searchによる比較を用いると、最悪の場合の必要な比較数は
S(n;n)
| =2 | n/2 Σ i=2 | ([log2(2i)]+1)+3 |
| =2n-1+2 | n/2 Σ i=2 | [log2(i)] |
ここで
| n/2 Σ i=2 | [log2(i)] |
| =(k+1)(m-1)+ | 2m-1-1 Σ i=2 | [log2(i)] |
| =(k+1)(m-1)+ | m-2 Σ i=1 | i・2i |
| =2+ | (n+2)
[log2(n/2)] 2 |
-2[log2(n)] |
| S(n;n)=2n+3+(n+2) | [ | log2 | ( | n 2 |
)] | -2[log2(2n)] |
nが奇数の場合、S(n-1;n)を計算します。
2m≦n=2m+2k+1<2m+1とすると,Binary Searchによる比較を用いると、最悪の場合の必要な比較数は
S(n-1;n)
| =2 | (n-1)/2 Σ i=1 | ([log2(2i+1)]+1) |
| =2n-2+2 | (n-1)/2 Σ i=1 | [log2(i)] |
| =2n+2+(n+1) | [ | log2 | ( | n-1 2 |
)] | -2[log2(2(n-1))] |
| =2n+2+(n+1) | [ | log2 | ( | n 2 |
)] | -2[log2(2n)] |
上記より
N(2n)
=n([log2(n)]+1)-2[log2(2n)]+1+2n+3+(n+2)[log2(n)-1]-2[log2(2n)]
=2(n+1)([log2(2n)])-2[log2(4n)] ; nが偶数。
N(2n)
=n([log2(n)]+1)-2[log2(2n)]+1+2n+2+(n+1)[log2(n)-1]-2[log2(2n)]+1
=(2n+1)([log2(2n)])-2[log2(4n)]+2 ; nが奇数。
N(2n) と T(2n)=2n([log2(4n)])-2[log2(4n)]+1を比較してみると
| 約2n- | 3[log2(n)] 2 | の差があることがわかります。 |
下記は N(2n)とT(2n)の比較数の計算結果です。
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| N(2n) | 1 | 4 | 8 | 14 | 21 | 26 | 31 | 40 | 46 | 56 | 62 | 72 | 78 |
| T(2n) | 1 | 5 | 11 | 17 | 25 | 33 | 41 | 49 | 59 | 69 | 79 | 89 | 99 |
実際、n=3の場合最小比較数は7回です。
n=4の場合最小比較数は11回のようです。
ですから、N(8)=14はまだまだ多いようです。
◆宮城県 アンパンマン さんからの解答。
Y.M.Ojisan さんの解答から一般解を予想すると
P(2n)
| = | n Σ i=1 | ([log2(i)]+2)-1 |
P(2n)は2n人がいるときの上位半数決定の最小対局数
予想最小対局数:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| P(2n) | 1 | 4 | 7 | 11 | 15 | 19 | 23 | 28 | 33 | 38 | 43 | 48 | 53 |
◆宮城県 アンパンマン さんからの解答。
最小対局数ではないのですが、とても少ない対局数の一つの方法です。
方法:
上位半数の人を一人ずつ決めます。
2n人がいる場合、n人勝てば上位半数になることを利用します。
対局数を少なくするためには、できるだけ対局した結果から多く利用します。
例として、n=9の場合を考えます。
図の緑色の線は新しい対局、黒い線は前の段階で対局したという意味です。
(分かりやすくするために、上位半数だと決定できた人はピンク色の点で表します。
上位半数との対局を表す線を消します。
Binary Treeの形は、子同士の対戦で勝者は親になります。
右側の図は、上位半数との対局を表す線を消したあとの図です。
最悪の場合を考えるため、勝者は一番多くの対戦をしてきた人とします。
(この場合、利用したい対局した結果が少なくなります。)
n=9の場合の対局数は
16+3+4+3*6=41局です。
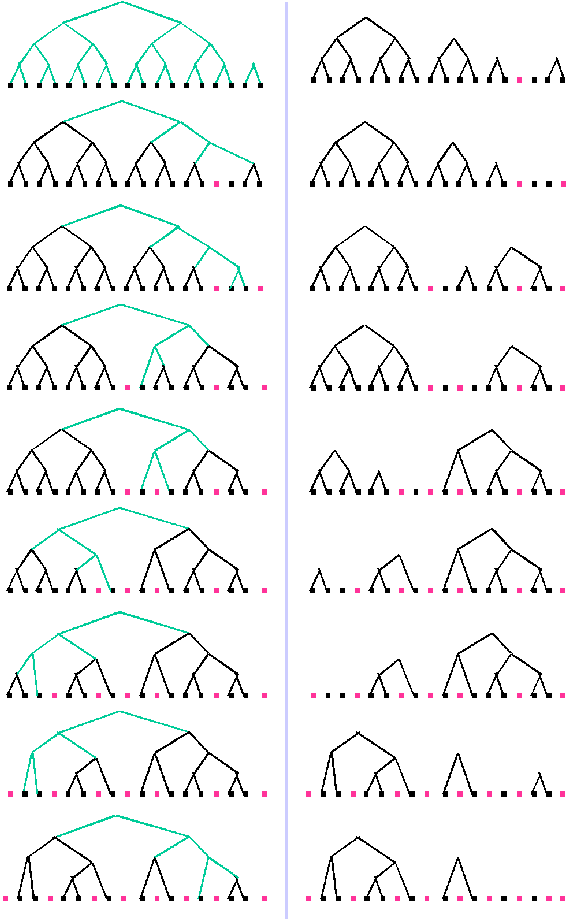
一般に nの場合、2m≦n=2m+k<2m+1を考えます。
(2n=2m+1+2k)
1)
まず、2m+1人をペアで戦わせます。
勝った人2m人をペアで対戦します。
このようにやっていくと最後に勝者一人が残ります。
(上位半数の人です)
(2m+1-1試合です。)
残りの2k人もペアで対戦します。
(k試合です。)
合計2m+1+k-1試合です。
2)
次はkペアの勝者から一人選んで 2m+1のグループと対戦します。
(m試合です)
勝者は上位半数の人です。
3)
1)と2)の2人の勝者のペアの敗者同士は対戦します。
勝った者は2m+1のグループと対戦します。
(全部でm+1試合です)
4)
2)と3)を繰り返し、全部で2k+1人の勝者が決まるまでやります。
( 2)と3) の繰り返しはk回です。)
5)
2m+1-1人の中からm試合で勝者が決まります。
これを 2m-k-1回繰り返すと 2m-k-1人の勝者が決まります。
( この2m-k-1人は上位半数の人達です。)
1)から5)まで選ばれた上位半数の人の合計は
1+2k+2m-k-1=2m+k=n人です。
全部の対局数は
R(2n)
=2m+1+k-1+m*k+(m+1)*k+(2m-k-1)
=2m+1+k-1+(m+1)k+(2m-1)m
=n[log2(4n)]-m-1
=(n-1)[log2(n)]+2n-1
計算結果:
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 50 | 100 | 5000 | 80000 |
| P(2n)(予想) | 4 | 7 | 11 | 15 | 19 | 23 | 28 | 33 | 38 | 43 | 48 | 53 | 58 | 63 | 292 | 679 | 61821 | 1308945 |
| R(2n) | 4 | 7 | 13 | 17 | 21 | 25 | 36 | 41 | 46 | 51 | 56 | 61 | 66 | 71 | 344 | 793 | 69987 | 1439983 |
計算結果からR(2n)はP(2n)(予想対局数)に近いです。
その差はおよそ2[log2(2n)]-2[log2(2n)]<2nです。
| ちなみに | lim n→∞ |
R(2n) P(2n) | =1。 |
R(2n)は順番付け(T(2n))のおよそ半分です。
この方法の良い点は少ない対局数保ちながらも誰と誰対戦すべきか簡単に決められることです。
| m人から上位k人(k≦ | m 2 | )を決定するときも簡単にできます。 |
| k> | m 2 | の場合も下位m-k人が決まれば上位k人も決まります。 |
ちなみに、P(2n)の規則性はもうちょっと複雑な気がします。
予想したP(2n)は正しくないかもしれませんが、
P(2n)はおよそ nlog2(n)は確かです。
◆愛知県 Y.M.Ojisan さんからの解答。
N=4 手順11回の場合で、他同様、最後まで左右対称の方法(つまり一本道の方法)があったので下記に報告します。
前回の方法では最後に上下対称を持ち込んでいました。
【N=6〜8】
N=6 の場合 アンパンマンさんのP予想より一回多い20回の方法がありました。
N=5までのように対称性が無く単純ではないので下記に表で示します。
なお、N=7の場合24回 N=8の場合30回の方法が確認されました。
もちろんPCで計算した結果ですが、とても虱潰しというわけには行かないので、手順はある程度決め打ちして得た中途半端な結果です。
まず10手使って下図の関係にする。
その後下表により手順をすすめると20回で完成。
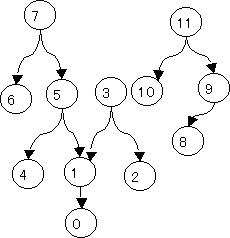
<19回の手発見(下記)により表は削除しました>
◆出題者のコメント。
具体的対局手順を検討したのではなく、一般化した手法で私なりに得た一般解によると、
大会参加者が2N人の時の求める最少対局数P(N)は以下の通りでした。
P( 1)= 1
P( 2)= 4
P( 3)= 7
P( 4)=11
P( 5)=15
P( 6)=20
P( 7)=25
P( 8)=29
P( 9)=35
P(10)=40
P(11)=45
P(12)=51
P(13)=56
P(14)=62
P(15)=68
出題範囲(4人〜10人)の人数では、Y.M.Ojisan さんの解答と同一です。
Y.M.Ojisan さんによると、N=7の時は24回の対局で十分なことが確認されたようですが、私の得た一般解とは異なります。
私の得た一般解の反例として、その対局手順を示して頂ければありがたいのですが・・
(私の得た一般解P(N)そのものは、正当性が確認されるまで控えます)
◆愛知県 Y.M.Ojisan さんからの解答。
【N=7対局データ】
リクエストにお答えして、N=7の24局の手を解答します。
手順が大きく複雑なのでエクセルファイル(14人対局.xls 約230kB)を添付いたします。
シート”OUT14”が手順データです。
あわせてサンプリングチェックのマクロを作成しました。
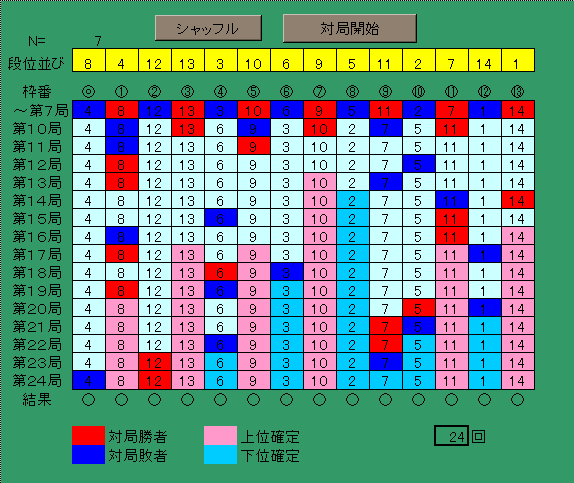
シート”CHECK”で起動ください。下図参照。
「シャッフル」をクリックすると黄色枠がランダムに97回互換されます。
「対局開始」をクリックすると、上位半数分けが実施されます。
意味は下図参照。
段位が大きい方が強い。
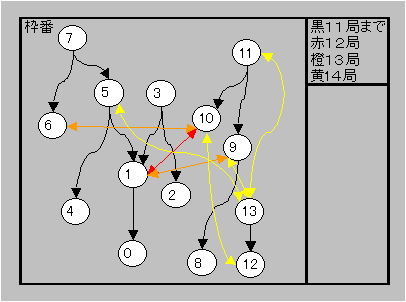
【補足】
最初に11局を行い、下図の黒矢印の関係に並べ替えます。
以後は対称性があるかどうか定かではないので、全部データに従って、手順を進めます。
【N=6対局データ】
N=6の場合にも19局の手があったので解答します。
手順が複雑なのでエクセルファイル(12人対局.xls 約80kB)を添付いたします。
シート”OUT12”が手順データです。
あわせてサンプリングチェックのマクロを作成しました。
シート”CHECK”で起動ください。
使い方はN=7とおなじです。
なお、前回解答の20局の手は削除していただきました。
最初の10局は同じです。
エクセル97以降をお持ちで無い方は、UpperHalf.lzh(約10kB)を解凍下さい。
データ部だけのテキストファイル 12人対局.txt と 14人対局.txt が出てきます。
【その他】
その後、N=8において、目標としていたの29局の手順を見つけました。
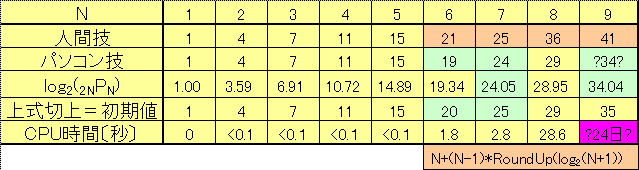
いろいろ出してきたので、結果を下表にまとめました。
探索プログラムの初期値として現在採用している実験式値と
出題者のP(N)は見えている範囲では一致しています。
また、N=6以降の人間技の値は、単純に
(1)N+1人のトーナメント(N局)を行い、上位1人を決める。
(2)トーナメントの欠員1人補充しては
最悪局数( log2(N+1)の切り上げ )を(N−1)回実施。
によっていますが、
これも何故か値だけはアンパンマンさんのR(2n)と一致しています。
【P.S.】
●N=7の手はN=8の29局を見つけるべく探索ソフトを改良している過程で出てきたものです。
「初期値」が一般解だろうと予想していたので、実は私もまだ半信半疑です。
サンプリング程度の検査では、今のところ例外(バグ)は出ていません。
N=6の場合も、念のため改良タイプで計算したら驚きの19回でした。
●表の初期値の切り上げ前値をみると、
N=7の場合以上にN=9の場合は限りなく34に近いので、これを見つけてやろうと、探索方法の抜本的改良を考えています。
現状の延長ではとんでもなく時間がかかりそうなので、一般解を開示していただけると、近道が見つけ易いです。
●式の見た目は違うのになぜかアンパンマン解とYM人間技解が一致しているのを突き詰めると、
N>0、K>1が整数のとき
logK(N+1)の切り上げ=1+logK(N)の切り捨て
が隠れていました。
◆広島県 清川 育男 さんからの解答。
参考になるかどうか確信がありませんが、議論に関心を持っています。
アンパンマンさんの予想に特に近い数列になります。
A001227(n) ID Number: A056548 Sequence: 0,1,4,7,11,15,19,23,29,32,37,43,47,52,58,62,68,73,79,84,90, 94,100,108,112,117,124,128,136,142,146,152,160,165,171,177, 183,188,196,202,208,215,219,227,233,237,247,253,259,263,272, 277,283,293,297,303,311,315 Name: Sum of round[n/k] for k>=1 where round[1/2]=0. Formula: a(n) =A056549(n)-A001227(n) See also: Cf. A006218, A056549. Keywords: easy,nonn Offset: 0 Author(s): Henry Bottomley (se16@btinternet.com), Jun 21 2000http://www.research.att.com/~njas/sequences/eisonline.html
◆出題者のコメント。
「Y.M.Ojisan さん」大変お手数をおかけしました。
それに解答を寄せてくださった方々、本当にありがとうございます。
実は、私もY.M.Ojisan さんの初期値が一般解だと信じて疑いませんでした。
[ log2(2NPN) ≦ k を満たす最小な整数k ]
おかげで、これは不正解であることが納得できました。
そこで、アンパンマンさんの予想式が、正解か又は正解に1番近いのだろうと思ったら、新たに「清川 育男 さん」より、その予想式と少しだけ違う数列が示されました。
どうも、この問題は思っていたよりずっと奧が深そうですね。
◆愛知県 Y.M.Ojisan さんからの解答。
【休憩室】
封じ手の考慮時間中、関連話題として、実用上の上位半数分けを少し考えました。
囲碁の名人対局のように2日もかけて、優劣判定をつける場合、最良手順P(n)を考えている時間は十分にあります。
でも比較が単順で、数が沢山ある場合はそうも言っていられません。
実際、全員の順位付けをするアルゴリズムとして「クイックソート(qsort)」等が標準的に存在している意義がそこにあるのでしょう。
下表はqsortの比較回数の期待値を求めたものですが、P(n)と比べれば効率が良いとはいえません。
ばらつき(標準偏差)は10%強でまあまあでしょうか。
| 2N個の全ソート | ||
| 2N | 最少比較 P(n) log2(2NP2N) |
Qsort 比較数期待値 ±標準偏差 |
| 2 | 1 | 1.0±0.0 |
| 4 | 5 | 4.8±0.9 |
| 6 | 10 | 10.3±1.8 |
| 8 | 16 | 16.9±2.9 |
| 10 | 22 | 24.4±3.9 |
| 12 | 29 | 32.7±5.0 |
| 14 | 37 | 41.5±6.2 |
| 16 | 45 | 50.9±7.3 |
| 18 | 53 | 60.8±8.5 |
| 20 | 62 | 71.1±9.7 |
| 22 | 70 | 81.8±10.8 |
| 24 | 80 | 92.8±12.1 |
| 26 | 89 | 104.2±13.2 |
| 28 | 98 | 115.8±14.5 |
| 30 | 108 | 127.7±15.7 |
さて、上位半数分けの場合ですが、プログラムにし易い方法として、
(1)冒頭に示した最悪N2の方法(Tdivideと呼ぶ)と
(2)人間技の方法 の期待値を下表に示します。
「Tivide」は期待値で評価すると最小手順数と競っており、多数組の分別が必要で平均値が期待できる場合は有効と考えられます。
ただし、ばらつき(標準偏差)がかなり大きく(約25%)、当てにならないという欠点があります。
一方「人間技」は期待値はすこし劣りますが、ばらつきが非常に小さく、少数組だけ分別が必要な場合には向いているでしょう。
| 2N個上位半数分別 | ||||
| N | Footmark P(n) log2(2NPN) |
AnPanMan 予想 (n+1)[log2(4n)]-2[log2(2n)]-1 |
Tdivide 比較数期待値 ±標準偏差 |
YM人間技 比較数期待値 ±標準偏差 |
| 1 | 1 | 1 | 1.0±0.0 | 1.0±0.0 |
| 2 | 4 | 4 | 3.7±0.5 | 3.7±0.2 |
| 3 | 7 | 7 | 7.2±1.3 | 7.0±0.0 |
| 4 | 11 | 11 | 11.1±2.4 | 11.2±0.7 |
| 5 | 15 | 15 | 15.4±3.5 | 15.7±0.9 |
| 6 | 20 | 19 | 19.9±4.7 | 20.3±0.6 |
| 7 | 25 | 23 | 24.5±6.0 | 25.0±0.0 |
| 8 | 29 | 28 | 29.3±7.3 | 30.6±1.2 |
| 9 | 35 | 33 | 34.1±8.6 | 36.2±1.9 |
| 10 | 40 | 38 | 39.0±9.9 | 41.9±2.2 |
| 11 | 45 | 43 | 44.0±11.3 | 47.7±2.2 |
| 12 | 51 | 48 | 49.1±12.6 | 53.5±2.0 |
| 13 | 56 | 53 | 54.2±14.0 | 59.3±1.5 |
| 14 | 62 | 58 | 59.3±15.3 | 65.1±0.8 |
| 15 | 68 | 63 | 64.5±16.7 | 71.0±0.0 |
◆出題者のコメント。
2N人とN人の全員順序付けする必要対局数の差になる筈と推論しましたが、Y.M.Ojisan さんがパソコン技で得た値が正解ならこれに間違いはありませんでした。
私の旧一般解は、計算を簡単にするために、
| log2(2N)!−log2N!=log2 | (2N)! N! |
以下、[X]↑は X 以上の整数で最小のものを表すものとします。
〔旧一般解〕
| P(N) = | [ | log2 | (2N)! N! | ]↑ |
これは結局
P(N) = [log2(2N)!−log2N!]↑ です。
〔新一般解〕
P(N) = [log2(2N)!]↑−[log2N!]↑
この〔新一般解〕は,Y.M.Ojisan さんがパソコン技で得た値と,示された範囲においてはすべて一致しています.