『ディオファントスの方程式』解答

◆広島県　清川　育男　さんからの解答。

【問題１】

ａ²＋ｂ²＝ａ＋ｂ＋２............1)

両辺に４を掛けて変形すると、
（２ａ−１）²＋（２ｂ−１）²＝１０
（２ａ−１＝１，２ｂ−１＝３）,（２ａ−１＝１，２ｂ−１＝−３）
（２ａ−１＝−１，２ｂ−１＝３）,（２ａ−１＝−１，２ｂ−１＝−３）
（２ａ−１＝３，２ｂ−１＝１）,（２ａ−１＝３，２ｂ−１＝−１）
（２ａ−１＝−３，２ｂ−１＝１）,（２ａ−１＝−３，２ｂ−１＝−１）

これを解くと、
（ａ＝１，ｂ＝２）,（ａ＝１，ｂ＝−１）,（ａ＝０，ｂ＝２）
（ａ＝０，ｂ＝−１）,（ａ＝２，ｂ＝１）,（ａ＝２，ｂ＝0）
（ａ＝−１，ｂ＝１）,（ａ＝−１，ｂ＝0）

　以上８通りあります。

【問題２】

３×２^a＋１＝ｂ²............１）
３×２^a＝ｂ²−１............２）
３×２^a＝（ｂ＋１）（ｂ−１）
ｂ＋１＝６、 ｂ＝５
６×４＝２４
２^a＝８， ａ＝３

ａ＝３，ｂ＝５

ｂ−１＝６，ｂ＝７
８×６＝４８， ２^a＝１６， ａ＝４

ａ＝４，ｂ＝７

ｂ＋１＝６ｍ，ｂ−１＝６ｍ
ｍ＝１ のときだけ成り立つ。
なぜなら、ｍ>１のときは、２以外の素因数がはいるから。　

　　　答え　（ａ＝３，ｂ＝５），（ａ＝４，ｂ＝７）

【問題４】

ａ²−２ｂ²＝１

（ｂ＝０，ａ＝１）,（ｂ＝０，ａ＝−１）,（ａ＝３，ｂ＝２）
（ａ＝−３，ｂ＝２）,（ａ＝３，ｂ＝−２）,（ａ＝−３，ｂ＝−２）

以上は暗算で解ると思います。
以下はテキストのカンニングです。

２は完全平方数でないので、正の整数解は、

（３＋２)ⁿ＝ａ_n＋ｂ_n..........１）

ｎ＝１
　３＋２＝ａ₁＋ｂ₁

　ａ₁＝３，ｂ₁＝２
　３²−２×２²＝１

ｎ＝２
　１７＋１２＝ａ₂＋ｂ₂

　ａ₂＝１7，ｂ₂＝１２
　１７²−２×１２²＝１

ｎ＝３
　９９＋７０＝ａ₃＋ｂ₃

　ａ₃＝９９，ｂ₃＝７０
　９９²−２×７０²＝１

ｎ＝４
　５７７＋４０８＝ａ₄＋ｂ₄

　ａ₄＝５７７，ｂ₄＝４０８
　５７７²−２×４０８²＝１

...............................
...............................

１）式を証明するとなるとゼロからのスタートでは無理なのでは？

【コメント】

　鮮やかな解答をいただきまして、ありがとうございます。
３題とも正解だと思います。
問題４については、１）式を仮定しなくても解けると思います。
方程式の解の数字をよく見ると分かるのですが、一つの解ａ₁、ｂ₁が分かると、それを用いて次の解は、簡単に計算することができるのです。
ぜひその関係を見つけてください。

◆広島県　清川　育男　さんからの解答。

【問題４】

　ご指摘のように漸化式がありますね。

ａ_n＝６×ａ_n-1-ａ_n-2
ｂ_n＝６×ｂ_n-1-ｂ_n-2

ａ₁＝１，ｂ₁＝０
ａ₂＝３，ｂ₂＝２
ａ₃＝１７，ｂ₃＝１２
ａ₄＝９９，ｂ₄＝７０
ａ₅＝５７７，ｂ₅＝４０８
ａ₆＝３３６３，ｂ₆＝２３７８
３３６３²−２×２３７８²＝１１３０９７６９−２×５６５４８８４＝１

キツネに化かされたような気分です。

　隣接３項間の漸化式について、数学１−Aの参考書に特性方程式というのがありました。
私が高校生のときは、習わなかったと思います。
今回の場合に適用すると以下のようになります。

（Ｘ−（３＋２））（Ｘ−（３−２））＝０

Ｘ²−６Ｘ＋１＝０。

ａ_n+2−６×ａ_n+1＋ａ_n＝０
ａ_n+2＝６×ａ_n+1−ａ_n

今の高校生は高度なテクニックを習うのですね。

【コメント】

さらにおまけをいうと、この問題の解は一次変換を用いて求めることもできます。

ａ_n+1＝Ｃ×ａ_n＋Ｄ×ｂ_n
ｂ_n+1＝Ｅ×ａ_n＋Ｆ×ｂ_n

定数Ｃ、Ｄ、Ｅ、Ｆを求めてみてください。

◆広島県　清川　育男　さんからの解答。

　Ｃ＝３，Ｄ＝４，Ｅ＝２，Ｆ＝３

ａ_n+1＝３×ａ_n＋４×ｂ_n

ｂ_n+1＝２×ａ_n＋３×ｂ_n

ｎ＝６，ａ₆＝３３６３，ｂ₆＝２３７８

ｎ＝７，
ａ₇＝３×３３６３＋４×２３７８＝１００８９＋９５１２＝１９６０１
ｂ₇＝２×３３６３＋３×２３７８＝６７２６＋７１３４＝１３８６０

　１９６０１²−２×１３８６０²
＝３８４１９９２０１−２×１９０２０９９６００
＝１

以上です。

意味は理解出来ません。奥が深いのは解りますが。

【コメント】

　行列を使って、一気に両方の一般項を求めた印象が強かったので出題したのですが、漸化式が既に求められているので、やはり蛇足でしたね。
さらに蛇足を言うと、この方程式はペルの方程式というそうです。
ペルは１７Ｃの英国の数学者です。

◆広島県　清川　育男　さんからの解答。

【問題３】

　対偶を証明する。
「ｃが合成数のとき、

１ ａ

−

１ ｂ

＝

１ ｃ

の解は１通りではない。」

ｃ＝ｐ×ｑ，　ｐ、ｑは素数とする。

１ ａ

−

１ ｂ

＝

１ ｐｑ

....1)

ｐ×ｑ（ｂ−ａ）＝ａ×ｂ.....2)

イ）
ａ＝ｐ×ａ1，ｂ＝ｑ×ｂ1 とおく。
1)式に代入する。
ｐ×ｑ（ｑ×ｂ1−ｐ×ａ1）＝（ｐ×ａ1）×（ｑ×ｂ1）
ｑ×ｂ1−ｐ×ａ1＝ａ1×ｂ1

ｂ1＝

ｐ×ａ1 ｑ−ａ1

1)式に代入する。

１ ｐ×ａ1

−

ｑ−ａ1 ｐ×ｑ×ａ1

＝	ｑ−（ｑ−ａ1） ｐ×ｑ×ａ1

＝

ａ1 ｐ×ｑ×ａ1

＝

１ ｐｑ

∴

１ ａ

−

１ ｂ

＝

１ ｃ

ロ）
ａ＝ｑ×ａ1，ｂ＝ｐ×ｂ1 とおく。

1)式に代入する。
ｐ×ｑ（ｐ×ｂ1−ｑ×ａ1）＝（ｑ×ａ1）×（ｐ×ｂ1）
ｐ×ｂ1−ｑ×ａ1＝ａ1×ｂ1

ｂ1＝

ｑ×ａ1 ｐ−ａ1

1)式に代入する。

１ ｑ×ａ1

−

ｐ−ａ1 ｐ×ｑ×ａ1

＝	ｐ−（ｐ−ａ1） ｐ×ｑ×ａ1

＝

ａ1 ｐ×ｑ×ａ1

＝

１ ｐｑ

∴

１ ａ

−

１ ｂ

＝

１ ｃ

　以上少なくとも２通りの解がある。

したがって

１ ａ

−

１ ｂ

＝

１ ｃ

の解が１通りのときｃは素数である。」

【コメント】

　確かに対偶を考える方が証明しやすいですね。
ついでにｃが素数の時は、１通りの解しかないことを示してくださると更に嬉しいです。

◆石川県　数学好き　さんからの解答。

【問題３】

「ｃが素数のとき、１通りの解しかない。」

証明
ｃは素数であるとする。

(ｂ−ａ)ｃ＝ａ×ｂであるから、
ａ×ｂはｃで割り切れる。

ｃは素数だから、ａまたはｂがｃで割り切れる。

ｂがｃで割り切れることは明らかである。
さもないとａ≧ｃとなり、

１ ａ

−

１ ｂ

＝

１ ｃ

は成立しない。

ｂ＝ｃｐとする。

１ ａ

−

１ ｂ

＝

１ ｃ

に代入して

ａ＝

ｃｐ ｐ＋１

...1)

1)より、ｃはｐ＋１で割り切れる。

一方　1)より(ｐ＋１)ａ＝ｃｐ。
ａはｃで割り切れず、ｃは素数だからｐ＋１はｃで割り切れる。
以上のことからｐ＋１＝ｃ。
つまりｐ＝ｃ−１である。

したがって

１ ｃ−１

−

１ ｃ(ｃ−１)

＝

１ ｃ

ｃが素数のとき、ａ＝ｃ−１，ｂ＝ｃ(ｃ−１)の１通りの解しかない。

◆『Mathematica on the Web』の解答。

問題１

解答

まず、変数 a について与式を解きます。

a は、整数ですからルートの中身は正である必要があります。

上のグラフより b は 2,1,0,-1 となるので、a を求めます。

よって答えは、

問題２

解答

まずは、与式を変形します。

右辺を因数分解します。

ここまでをまとめると以下の式を得ます。これからわかるように、右辺のうち (b-1) か (b+1) は 3 の倍数である必要があります。

仮に (b-1) が 3 であるとすると、

つまり、(b+1) = 5 となり 2 の倍数となりません。逆を考えます。

(b-1)=1 となりますが、a=0 となり a が自然数になりません。

以上により、(b-1) か (b+1) は 6 の倍数である必要があります。

(b-1)=6m もしくは (b+1)=6m から、 (b+1)=6m+2、(b-1)=6m-2 を得ます。

よって、(a,b)=(3,5),(4,7)

補足

6m が 2 の累乗であるときに、6m±2も 2の累乗であるためには、m が小さい必要があります。なぜなら、

問題３

解答

与式をわかり易く、左辺をまとめます。

辺々に a b c をかけます。次の式が得られます。

直接証明するのは悶しいため対偶である
『c が合成数のとき、与式を満たす自然数は一通りに定まらない』
を以下で証明します。まず、c は合成数ですから次のように分解されます。

また、式(1)の左辺から右辺を引いたものを f とします。
ｆ= 0 なる a, b, c が与式を満たす自然数解となります。

まず、a, b が次のような場合に与式を満たすことを示します。

式(3)より得られる関係を f に代入していきます。

式(3)の a, b が与式を満たすことがわかりました。

次に、a, b が次のような場合に与式を満たすことを示します。

式(4)より得られる関係を f に代入していきます。

式(4)の a, b が与式を満たすことがわかりました。

q = p のときの考察

以上により、q ≠ p ならば解が２つ存在し対偶は正しいことになります。
しかしながら、q = p であれば解は必ずしも２つあるとは言えません。

p=q かつ A=B ならば、対偶は明らかに正しいため以下では A≠Bとします。

そこで、a, b が次のような場合に与式を満たすことを示します。

式(5)より得られる関係を f に代入していきます。

式(5)の a, b が与式を満たすことがわかりました。

次に、a, b が次のような場合に与式を満たすことを示します。

式(6)より得られる関係を f に代入していきます。

式(6)の a, b が与式を満たすことがわかりました。

〜結論〜

問題４

方程式 を満たす、整数 a, b を求めてください。

解答

次のような方程式を Pell の方程式と呼びます。

（ここで M は平方数でない正整数で c=±1）

まず、数列の一般項を求めるパッケージを読み込みます。

次に、式 (8),(9) より求まる一般項を関数 RSolveで計算します。

一般解の関数を定義します。

この関数を使って１０個の解を求めてみます。

付録

数学的でなくてもよければ、次のようにして求められます。

◆東京都の中学校１年生　安里歩安彼　さんからの解答。

【問題４】

a²−kb²＝１という形の方程式について述べたいと思います。

a²−kb²＝１…(1)と、

は、同値である。

さて、よって、一般にZ(√k）と言う環(環Aとする）においての、１の素因数分解の仕方を考察することになる。

２乗しているので、a,bともに正の数の場合だけ考えればよい。
いま、a,bともに最小な数の組を、a₁,b₁であるとし、
a₁＋√kb₁を、εとする。
（実は、このとき、εは環Aにおける、１の約数で、１以上のものの最小値…★）

このとき、次のことが分かる。

εⁿの形の数は、すべて、環Aにおいての、１の約数である。…(3)

略証：

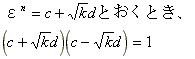
が成り立つことが、数学的帰納法によって、簡単に証明できるから。

さて、逆に、
εⁿの形以外の数は、環Aにおいて、１の約数になり得ない…(4)

証明：いま、δが、１の約数であり、

ε^m＜δ＜ε^m+1…(5)である。

当然、δ/ε^m+1も、１の約数となり得るので…これをγとおくと、
γ＜εとなり、★に矛盾する。
よって示された。

この(3)、(4)をつかえば、一般に、(1)の形の問いに答えることができます。

◆海外　Londonたぬき　さんからの解答。

【問題１】

式を下記の様に変形して

a²+b²=a+b+2
a²-a+b²-b=2

(a-

1 2

)

2

-

1 4

+(b-

1 2

)

2

-

1 4

=2

(a-

1 2

)

2

+(b-

1 2

)

2

=

10 4

この式は、a,bを座標軸とする平面上で、

(

1 2

，

1 2

)を中心とし、半径

(

10 4

)

0.5

(=約1.6)の円周を表す。

よって、求めるa,bはこの円周上に存在する。

この式を満たすaは、約-1.1≦a≦約2.1、
この範囲に含まれる整数は-1，0, 1, 2に限られる。

それぞれの場合にbの値を求めると、

a=-1の場合: 1+b²=-1+b+2、よって b=0,1

a=0の場合：b²=b+2、よってb=-1,2

a=1の場合: 1+b²=1+b+2、よってb=-1,2

a=2の場合: 4+b²=2+b+2、よってb=0,1

以上求める解は8通り。

昔（高校時代)、同様の問題を解いた記憶を辿りながら解いてみました。

　『ディオファントスの方程式』へ

　数学の部屋へもどる