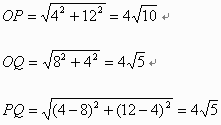
◆東京都 千葉 英伸 さんからの解答。
【問題1】
△OPQの3辺の長さを求めてみると、
となり、辺の比が1:1:  の直角二等辺三角形なので、
の直角二等辺三角形なので、
∠POQ=45゚
A1 は直線OP:y=3χと放物線y=χ2の交点で、題意から原点Oとは異なる点なので、
A1=(3,9)
同様に、C1 は
| OQ:y= |
1 ―― 2 | χ |
| C1=( |
1 ―― 2 | , |
1 ―― 4 | ) |
【問題の考察】
先へ進む前に、この問題の性質を考えてみる。
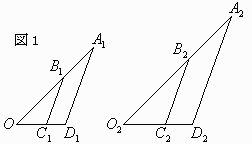
まず、直線 A2B2が原点を通ることを示す。
直線A2B2と直線C2D2の交点をO2とする。
問題から、
① 四角形A1B1C1D1と四角形A2B2C2D2が相似
②A1D1とB1C1は平行
(①よりA2D2とB2C2も平行)
この条件をもとに、"図形"的に考えると、
①より対応する角はそれぞれ等しく、②の条件とあわせれば、図1の4つの三角形はすべて相似であることがわかる。
つまり、
△OA1D1∽△OB1C1∽△O2A2D2∽△O2B2C2
さらに、①より対応する辺どうしの比も等しいから、
OB1:B1A1 =OC1:C1D1=O2C2:C2D2
ここで、C2,D2 はもともとB1,A1と同一の点なので
OB1=O2B1
つまり、O2と原点Oとは一致する。
(ひょっとして、自明かな?)
図1では、説明のために線分OA1上にB1をとっているが、それ以外の場合も同様。
一般のnについても、同様の操作を繰り返すだけなので、
図1のように原点と四角形Kn でつくられる三角形はすべて相似で、
直線AnBnは原点を通ることがわかる。
また、∠AnODn=∠POQ=45゚(問題1より)なので、
問題の操作によって、四角形Knは原点を中心に45゚ずつ分けられた8つの象限を順番に移動し、8回の操作で元の象限に戻ってくる。
【問題2】
上記の考察から、直線A2B2は原点を通り、直線OQと直交する。
従って、直線 A2B2: y=-2χとなる。
今、A2は放物線y=χ 2上にあるので、
その座標は、(-2,4)。
また、明らかに
△A1OC1∽△A2OC2なので、
OA1:OC1=OA2:OC2
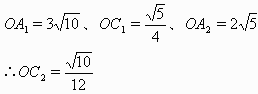
OC2を斜辺とし、x軸、y軸に平行な辺でつくられる直角三角形を考えると、
x軸に平行な辺、y軸に平行な辺、OC2 の比は、
1:3: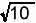 なので、
なので、
C2=B1の座標は、
| B1= | ( | 1 ―― 12 | , |
1 ―― 4 | ) |
【問題3】
四角形 A1B1C1D1と
四角形 A2B2C2D2が合同になるような
B1を求めればよい。
△A1OC1≡△A2OC2となるような条件は、
OC2=OC1= |
 ―― 4 |
あとは、問題2と同様にして、
B1= | ( |
 ―― 8 | , |
3 ――― 8 | ) |
【問題4】
まず、比の条件からA9の座標を求めてみる。
考察から、対応する長さの比は等しく、
OAn:ODn=OA1:OD1=m:1なので、
OAn=mODn=mOAn-1=・・・=mn-1OA1 (*)
A9は8回目の操作だから直線OA1上にあり、
OA9=m8OA1
∴A9=(3m8,9m8)
このA9は
| 放物線y= | χ2 ―― m8 | 上にある。 |
| 放物線y= | χ2 ―― m8 | と |
| 直線OQ:y= | 1 ―― 2 | χ |
D1= | ( | m8 ―― 2 | , |
m8 ―― 4 | ) |
次にC9の座標を求めてみると、
四角形A1B1C1D1と四角形A9B9C9D9は相似だから、
OA1:OA9=OC1:OC9=1:m8
∴C9= | ( | m8 ―― 2 | , |
m8 ―― 4 | ) |
つまり、D1とC9は一致するので、
線分A1D1と線分B9C9も一致し、隙間ができることはなく、重なることもない。
さらに、D1の座標がわかったので、
OA1:OD1=m:1から、mを求めると、
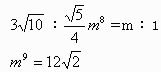
よって、m>1なので、(*)により、
OAn→∞(n→∞)
各Knの相似性から、原点の周りをのぞいて、隙間ができることはなく、重なることもなく座標平面を覆う。
【問題5】
m9=12 より、
より、
m8=12.3897723837・・・
計算は省きますが(^_^;)、
点(1999,1999)は K25に含まれる。