『放物線の弧と円弧の関係』解答

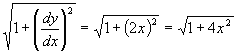
◆愛知県　juin さんからの解答。

【問題１】

y=x2を微分して、

dy dx

=2x.

線素は

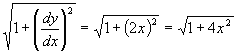
となる。

(0,0)から(1,1)までの長さは、線素をx=0からx=1まで積分して求める。

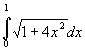　となる。

Newtonの方法で積分します。

x=とし、0≦y≦u²で長さを求めます。

dy dx

=

1 2

長さは、となる。

4y=zとして、

1 4

=∫z-1/2(z+1)1/2dz

z=

1 t

として積分は、 -∫t-2(t+1)1/2dt

t+1=uとして、積分は、

-∫(u-1)^-2u^1/2du

u=s2として、-∫

2s2 (s2-1)2

dsとなる。

分母、分子とも整式だから部分分数分解して積分できる。

元の変数yに戻すと、長さは

y=u²を代入して、

答え　　となる。

例えば、(0,0)から(1,1)までの曲線の長さは、

u=1として、

1 2

-

1 4

log(-2)となる。

　『放物線の弧と円弧の関係』へ

　数学の部屋へもどる