4k
◆東京都 梟 さんからの解答。
【問題1】
(1)
[m n]をm、nの最大公約数とする
●m>nのとき
c(k)=c(k−1)−b(k−1)とb(k)の大きいほう
b(k)=c(k−1)−b(k−1)とb(k)の小さいほう
c(1)=m
b(1)=m
の漸化式で与えられる数列を考える。
ユークリッドの互除法により
[m n]=[c(1) d(1)]=[c(k) d(k)]である。
また、c(k)=d(k)なるkが存在し、
そのときのc(k)がm、nの最大公約数である。・・・A
c(1)、d(1)ともにxm+ynの形で表せる
(x、yともに、ある整数)・・・1
c(k)、d(k)ともに上の形で表せるとき
c(k)=pm+qn
d(k)=rm+sn(pqrsともに整数)と置くと
c(k+1)=rm+sn または (p−r)m+(qーs)n
d(k+1)=rm+sn または (p−r)m+(qーs)n
であり、いずれにせよ、c(k+1)、d(k+1)ともに
xm+dmの形で表せる・・・2
1,2により任意のkに対してc(k+1)、d(k+1)ともに
xm+ymの形で表せる。・・・3
Aとm、nが互いに素であることから
c(k)=1であるようなkが存在する。
このときc(k)=vm+wn=1・・・3とおく。
大小関係から明らかにvw<0である。
w<0のとき
v=a、w=bと置けば与式は成立する。
また、v<0のとき、3の両辺を自乗すると
(mv2)m+(2vmw+nw2)n=1
mv2>0
であるから大小関係より(2vmw+nw2)<0である。
mv2=a
2vmw+nw2=−b
と置けば、与式は成立する
●n>mのときも、同様に証明できる。
(2)
背理法で示す。
| x= | b a | が方程式の解であると仮定する。 |
このとき両辺にakを掛けると
| 方程式はb( | k Σ n=1 | gnbk-nan-1 | ) | =−ak |
ところが、左辺は(1ではない整数)×整数の形をしており、
かつakはbを因数に含まない。
これは矛盾。
よって、与えられた方程式が有理数の解を持つのなら
| その解は | 1 r | の形をしている。 |
【問題2】
(1)
k=1の時、明らか
k=lの時coskαがcosαの多項式で表せ、
sinlαがsinα×cosαの多項式で表せると仮定する。
cos(l+1)α
=f(cosα)cosα+g(cosα)sinα・sinα
=f(cosα)cosα+g(cosα)(1-cosα・cosα)
sin(l+1)α
=sin(lα)cosα+cos(lα)sinα
=sinα(g(cosα)cosα+f(cosα))
となりいずれの場合も成立。
以上で、与えられた命題は証明された。
(2)
k=1のとき明らか。
k=2l-1のとき成立すると仮定する。
(1)の結果と加法定理より
cos(2l+1)α
=cosαh(cosα)cos2α-sinαg(cosα)sin2α
=cosαh(cosα)cos2α-sinα*sinαg(cosα)cosα
cos2α、sinα*sinαがcosαの多項式で表せることにより
cos(2l+1)αがcosα×cosαの多項式で表せる
以上により与えられた命題は証明された。
命題A
任意の整数kに対し、coskθが無理数ならcosθは無理数
証明
問題2の1)の( )の中身の対偶を取れば明らか。
【問題3】
(1)
背理法で示す
a、bは任意の0でない整数。
また互いに素である2整数m、nに対し
ユークリッドの互除法の特殊解ma+nb=1のa,bどちらかが0である場合題意を満たすことは明らかなので、以下の議論でm、nはそのような組み合わせではない。
| 一般に cos( | 1 n |
)πが無理数のとき |
| cos(a+ | 1 n |
)π=cos( | 1 n |
)π or −cos( | 1 n |
)π |
命題Aより、任意の0でない整数bに対して
| cosθが無理数ならcos( | 1 b |
)θも無理数。 |
| よって、cos | 1 b |
(a+ | 1 n |
)π も無理数。 |
問題1の(1)より
m、nに対し、mx=ny+1となる整数x、yが存在する。
x=b、y=aと置くと
| m n |
= | 1 b |
(a+ | 1 n |
)である。 |
以上から命題は証明された。
(2)
n=4k(kはある整数)とおく。
| cos( | k 4k |
)π= | 1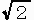 |
(3)
| y=cosxが0<x< | π 2 |
で単調減少だから |
| cos | π n |
> | cos | π 3 |
= | 1 2 |
・・・(1) |
ところで問題2の(2)より
| cos n( | π n |
)=1は問題1の(2)の形の方程式である |
| これが有理数解を持つなら、それは | 1 r |
の形をしていなければならないが |
(4)
nが4の倍数のとき(2)の結果より題意は明らかに成り立つ。
以下nは4の倍数ではない10以上の偶数として議論を進める。
nの因数に5以上の奇数(k)が含まれているとき、kは奇数だから
| cos | 2π 2k |
= | cos | π k |
は無理数。 |
(3)の結果より)
| よって問題2(2)の結果よりcos | π 2k |
は無理数。 |
また、kが5以下の奇数の場合、nは10未満。
よって題意は証明された。
(5)
| 3より cos | π n |
が有理数となるnは奇数なら1,3でなければならない。 |
| 4、2より cos | π n |
が有理数となるnは偶数なら2、6で無ければならない。 |
| cos | π 6 |
は | 2 |
で無理数。 |
| よって cos | π n |
が有理数になるならnは1,2,3であることが必要。 |
| cos | π n |
はそれぞれ−1、0、 | 1 2 |
で確かに有理数。 |
(6)
問題2の(1)と問題3の(1)より
| cos | mπ n |
が有理数⇔cos | π n |
問題3の(5)より
| cos | π n |
が有理数⇔n=1、2、3 |
| cos | mπ n |
⇔cos | π n |
⇔n=1、2、3 |
【問題4】
(1)
このとき整数l、m、nをつかって
a=lk、b=mk、c=nk と置ける。
余弦定理により
cosA
| = | k2(m2+n2−l2) 2mnk2 |
| = | m2+n2−l2 2mn |
同様にcosB、cosCについても証明できる
(2)
ある整数l、m、nをもちいて
A=xπ、B=yπ、C=π−xπ−yπ
A:B:C=x:y:1−x−y=l:m:nとおける。
よってxm=ly、yn=m−xm−ym
| よってy= | m l+m+n |
となりBは有理数×πの形で表せる
同様にA、Cについても
| A= | lπ l+m+n |
、C= | nπ l+m+n | とかける。 |
(3)
(2)かつ(1)のとき、問題3(6)の結果より
| A、B、Cはπ、 | π 2 |
、 | π 3 |
のいずれかの倍数。 |
| しかし、その最小値 | π 3 |
の3倍がπであることを考えると |
| A=B=C= | π 3 |
となるものしかない。 |