◆静岡県 ヨッシー さんからの解答。
【問題1】
凹部のある図形や、穴の空いた図形については、まだわかりません。
凹部も穴もない図形について考えます。
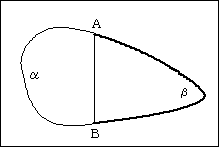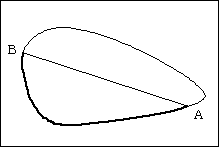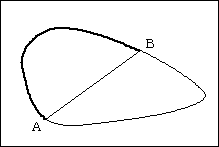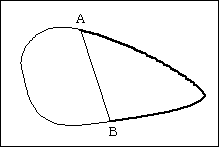
図形の周上の1点をAとするとき、点Aを通りこの図形の面積を2等分する直線AB(点Bは図形の周上のもう一方の点)を引くことは出来ます。
この時、点Aから点Bまでを周に沿っていく経路の長さの片方をα、他方をβとします。
ただしα≦βとします。
α=βであれば、題意を満たす直線Iが存在したことになります。
α≠βの時、周の長さの半分γに対して、
α<γ<βとなります。
今、点Aを周に沿って動かし、その都度、面積を2等分する直線ABを引くとき、点Aが最初に点Bがあった位置に来るまでに、点Aから点Bまでの経路の長さは、αからβへ、他方はβからαへ連続的に変化します。
その途中で、必ず経路の長さがγに一致するところがあるので、題意を満たす直線Iは必ず存在します。

【問題2】
(補題1)
となりあう2辺の長さの和が一定のとき、2辺の長さが等しいときが面積最大になる。
(証明)
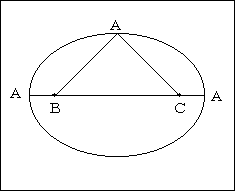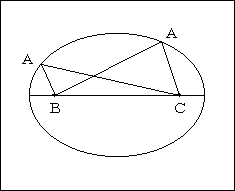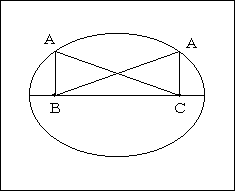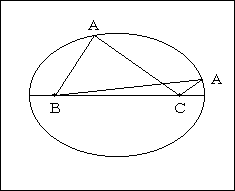
三角形ABCにおいて、辺BCを固定し、
AB+ACを一定にしたまま点Aを動かすと、点Aは、2点B、Cを焦点とした楕円の上を動き、三角形ABCの面積が最大(高さが最大)になるのは、
AB=AC のとき(点Aが短軸上にあるとき)である。
(補題2)
四角形以上の多角形で、連続する3つの辺の長さが等しいとき、その間の2つの角が等しいとき、面積最大になる。
(証明)
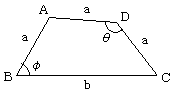
図のような、四角形ABCDにおいて、辺BCを固定し、
AB=CD=DA=a を保ちながら、点A、Dが動くとする
(ただし、四角形ABCDは凹四角形にならないとする)。
このとき、図のように角θ、φをとると、
対角線ACを、三角形ABC、三角形ACDにおける余弦定理で表すと、
AC2=a2+a2−2a2cosθ
AC2=a2+b2−2abcosφ
これより、
|
a2−b2 ―――――― 2 | =a2cosθ−abcosφ・・・(1) |
一方、四角形ABCDの面積をSとすると、
S=△ACD+△ABC
| = |
1 ―― 2 | (a2sinθ+absinφ) |
2S=a2sinθ+absinφ ・・・(2)
(1)と(2)をそれぞれ2乗して加えると、
| 4S2+ |
(a2−b2)2 ―――――― 4 |
| 4S2= |
3a4 ―――― 4 | − |
b4 ――― 4 | + |
3a2b2 ――――― 2 | − | 2a3bcos(θ+φ) |
よって、面積Sが最大になるのは、
cos(θ+φ)=−1
のとき、つまり、θ+φ=180°のとき。
このとき、四角形ABCDは円に内接し、∠BADと∠ADCは等しくなる。
(補題1)(補題2)より、
n角形の辺の長さの和が一定(=1)のとき、面積が最大となるのは、正n角形のときであるといえる。