『右折禁止の平安京』解答

◆愛知県　Y.M.Ojisan さんからの解答。

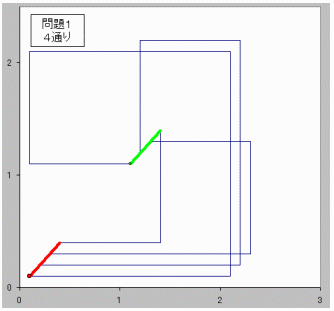
【問題１】

（ｍ,ｎ）＝（２，２）のとき、
格子点（０，０）から格子点（１，１）に行く方法は４通り。
下図参照。

なお、赤：出発　緑到着位置です。

【問題２】

（ｍ,ｎ）＝（３，３）のとき、
格子点（０，０）から格子点（３，３）に行く方法は１１通り。
下図参照

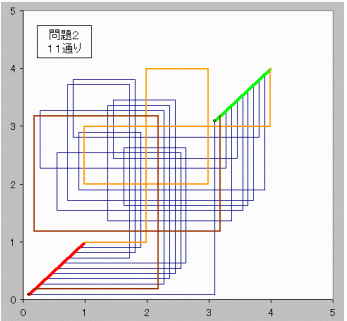
なお、赤：出発　緑到着位置です。
茶色経路は最長の一つ、橙色経路は左折回数最大の一つです。

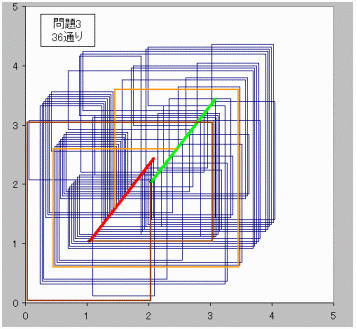
【問題３】

（ｍ,ｎ）＝（３，３）のとき、
格子点（１，１）から格子点（２，２）に行く方法は３６通り。

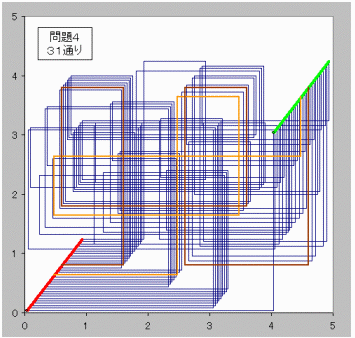
【問題４】

（ｍ,ｎ）＝（４，３）のとき、
格子点（０，０）から格子点（４，３）に行く方法は３１通り。

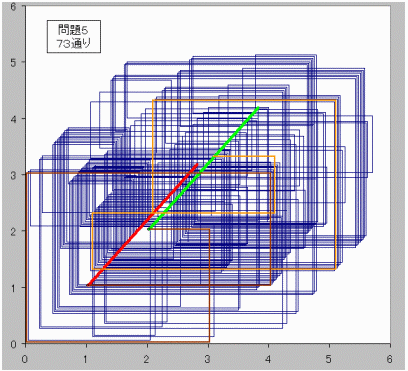
【問題５】

（ｍ,ｎ）＝（４，３）のとき、
格子点（１，１）から格子点（２，２）に行く方法は７３通り。

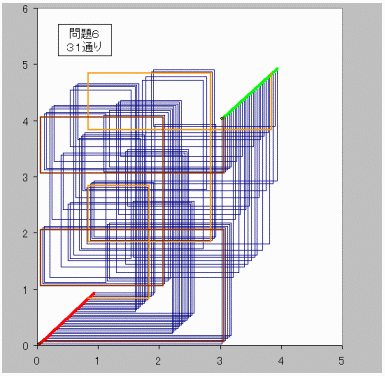
【問題６】

（ｍ,ｎ）＝（３，４）のとき、
格子点（０，０）から格子点（３，４）に行く方法は ３１通り。

【問題７】

（ｍ,ｎ）＝（３，４）のとき、
格子点（１，１）から格子点（２，２）に行く方法は ６８通り。

【感想と数値計算法】

　問題８と９は出来ませんでした｡
ここに示した解は計全部算機による結果です｡

ちょっと前にTV番組ですがTOKIOが２グループに分かれて、伊豆から東京タワーまで右折しないで自動車で競争するのがありました｡

　車の渋滞の原因の大きなものに右折車があります。
朝などある交差点では１回の信号で２〜３台しか進みません。
都市部では全部右折禁止にすれば、渋滞が減るかも。
そういった意味で結構現実的な問題かなと思います｡

また、平安京は我が故郷ですので、結構考えたのですが一般解は？？？でした。

　現実的問題としてはとりあえず計算機で解ければ良いので、プログラムを作成しました｡
ロジックはレトロにしてみました。
今を去る うん十年前高校生のころ、NHK教育TVでFORTRAN講座がありました。
例として「ペントミノ（パズル）の解を全部求める」というのがあって、当時の少ないメモリと遅いＣＰＵ用にとても美しいというか無駄のないプログラムであり大きな影響を受けましたが、その方法をベースにしました。

概要を以下に示します｡

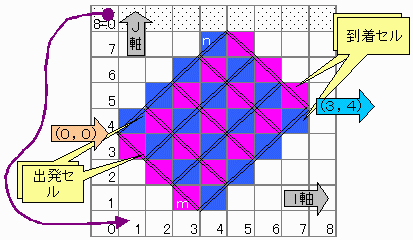
まず、通過通路をチェックするメモリが必要ですが、単純に考えると縦用と横用２個が２次元的に必要です｡
でも上図（ｍ＝３、ｎ＝４）の様に４５度倒し、チェッカーボード上に置くと図のように統一的に扱えます｡
ボードの大きさは
（ｍ＋ｎ＋２）×（ｍ＋ｎ＋１）

次に移動方向です。
絶対的には４方向がありますが、下表のように前回の方向に対しては直進左折の２種しか選択できません｡
これは0/1で表現することが出来ます｡

		今回移動可能方向＆セル
移動 番号	前回移 動方向	(-1，1)	(1、1)	(1，-1)	(-1、-1)	(任意)
0	(-1，1)	○	○	×	×	×
1	(1、1)	×	○	○	×	×
2	(1，-1)	×	×	○	○	×
3	(-1、-1)	○	×	×	○	×

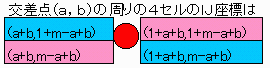
さらに位置を表現する方法として、下表のようにＩＪ座標を合成して、チェッカーボードを１次元の配列にします。
こうすると「移動」は一回の足し算で実現され、計算時間が短縮されます。

移動番号	座標表現	I　軸座標×P	＋Ｊ軸座標
0	(−１，１)	−1×P	＋１
1	(１、１)	1×P	＋１
2	(１，−１)	1×P	−１
3	(−１、−１)	−1×P	−１

Ｐ＝ｎ＋ｍ＋１

そしてメモリには

未通過　＝０　　　　　≦０

到着セル＝−１　　　　≦０

通過済み(通過番号)　　＞０

通路なし=Ｐ＊Ｐ　　　 ＞０

を記入して置／行きます｡

ただし、出発位置・到着位値は格子点でありチェッカーボードのセルではないので、出発格子点まわりの４つのセルのいずれかから出発し、到着格子点まわりの４つのセルのいずれかに到着する道順を探索します｡

【大きな領域での計算結果】

　京都の碁盤の目は今では論理性が崩れています｡
東西筋は　「。。姉三六角蛸錦。。」というふうに歌になっていますが、蛸薬師・錦小路など車では通りにくいか通れない小路です｡

大きくてほぼ端から端まで通じている道だけを数えて　Ｍ＝７　Ｎ＝８　とします。下記

私の旧実家はＭｓ＝０　Ｎｓ＝７付近にありました。
大学はＭｅ＝７、Ｎｅ＝８にあります｡

　家から大学まで右折禁止で行く方法はプログラムで計算すると、
全部で　なんと22,2784,2907とおり　でした。

なお、探索時間は500MHzＰＣですが１７時間もかかり、単なるしらみつぶしではこれ以上大きいのは無理。

通りは

西から：西大路　七本松　千本−大宮　　　堀川　烏丸　河原町　川端　東山
北から：今出川　丸太町　御池(一部迂回)　三条　四条　五条　　七条　九条　十条

三条通りは途中に商店街があって本当は直行できませんが、加茂川にかかる橋があるので採用しました。
二条城のある二条通りはくねくね曲がった路地のような通りに落ちぶれています。

　『右折禁止の平安京』へ

　数学の部屋へもどる