◆山形県の高校生 ice-tea さんからの解答。
【証明】

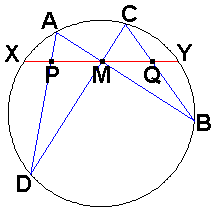
図の円の中心をOとすると
∠OMQ=OMP=90°なので三平方の定理より
OP2=OM2+MP2
OQ2=OM2+MQ2
それぞれ足して
OP2+OQ2=2OM2+MP2+MQ2
となるので中線定理よりMがPQの中点であるには
MP2=MQ2 すなわち
MP=MQ
◆宮城県 甘泉法師 さんからの解答。
xy座標の原点を中心とする半径1の円で考える。
点M(0,d)とおくと
直線XY y=d
直線AB y=ax + d
直線CD y=bx + d
直線ABと円の交点のx座標をあらわす方程式
(ax + d)2 + x2 = 1の解を
α,β,0<aα として
点A(α,aα+d) 点B(β,aβ+d)
同様に、方程式(bx + d)2 + x2 = 1 の解を
γ,δ,0<bγ として
点C(γ,bγ+d) 点D(δ,bδ+d)
直線AD{ y -(aα+d)}(α-δ)=(aα-bδ)(x−α)
点Pのx座標は、上の式にy=dを代入して
| x= | (a-b)αδ aα-bδ |
| x= | (a-b)βγ aβ-bγ |
f=(aβ-bγ)αδ + βγ(aα-bδ)とおくと
2次方程式の解と係数の関係からf=0
よってPM=QM
◆出題者のコメント。
ice-teaさん、甘泉法師さん、解答ありがとうございます。
ただ、ice-teaさんの証明は、証明すべきことを前提にして証明しているようなもので、証明になってないですね。
MがPQの中点であれば中線定理が成立するので、
確かに (MP)2=(MQ)2 です。
(もっとも、MがPQの中点であれば、中線定理を使うまでもなく、明らかに MP=MQ ですが…。)
しかし、MがPQの中点であることを証明しなければならない筈です。
甘泉法師さんの証明は、流石に鮮やかですね。
こんなにスマートな証明があるとは驚きです。
◆東京都の高校生 もやし さんからの解答。
【証明】
点Mを通る直径について点Dと対称な点をEとする。
明らかに点Eはこの円の円周上にある。
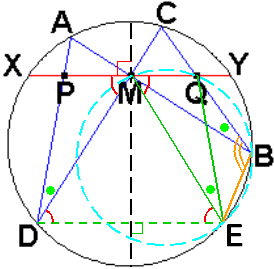
対称性から、MD=ME…(1),
∠MDE=∠MED…(2),
∠PMD=∠QME…(3)
XY//DEより、∠QME=∠MED…(4)
(2),(4)から、∠MDE=∠QME…(5)
また、四角形BCDEは円に内接するので、
∠MDE+∠QBE=180°
これと(5)より、∠QME+∠QBE=180°
よって、対角の和が180°なので、四角形BQMEは円に内接する。
その円において、円周角の定理より、
∠MBQ=∠MEQ…(6)
また、もとの円において、円周角の定理より、
∠MDP=∠MBQ
これと(6)より、∠MDP=∠MEQ…(7)
ここで、△PDMと△QEMにおいて、
(1),(3),(7)より、二角夾辺相等より、
△PDM≡△QEM
よって、PM=QM
[証明終]
ちなみにこれは、『胡蝶定理』といいます。
◆出題者のコメント。
もやしさん、解答ありがとうございます。
それにしても、目が眩むほど鮮やかな証明ですね。
(しかも初等幾何だけで…。)
『胡蝶定理』って言うんですか。
1つ勉強になりました。