◆山梨県 Footmark さんからの解答。
【問題1】
【答え】
6回
【考察】
まず、5人の旦那さんを任意に横1列にさせます。
この時の5人の旦那さんを、左から 0,1,2,3,4 とします。
(奥さん達も自分の旦那さんと同じに表すものとします。)
この時、P組が一致したものとします。
P=5なら、1回で終了です。
P≠5なら、1番左の旦那さん1人を1番右に移します。
旦那さん達の並びは、左から 1,2,3,4,0 です。
この時、Q組が一致したものとします。
Q=5なら、2回で終了です。
Q≠5なら、P=Q=1 の時以外はさらに1番左の旦那さん1人を1番右に移します。
旦那さん達の並びは、左から 2,3,4,0,1 です。
この時、R組が一致したものとします。
R=5なら、3回で終了です。
仮に、同様な入れ替えをもう2回させて試行したものとすると、5回の並びで各奥さんは全員の旦那さんと向かい合います。
ところが自分の旦那さんは1人ですから、すべての奥さんが1回だけ一致します。
ですから、5回の試行での一致組数の合計は5組になる筈です。
また、ここで5回の一致組数の組合せを考えてみます。
5回目の一致組数の後に1回目の一致組数が続くように5つの一致組数を円順列に並べます。
すると、奥さん達の並びには関係なく時計回りにある5つの一致組数の並びは必ず反時計回りにもあります。(証明省略)
つまり、円順列においてその前後の一致組数が対象になる一致組数が少なくとも1つは存在します。
以上の2点より、1回目〜3回目の一致組数より 4回目,5回目の一致組数は一意に得られます。
ただし、1回目,2回目の一致組数さえ得れば 3回目〜5回目の一致組数が得られるものもあります。

ケース04の時は、同様な移動を多くとも今後2回させれば、必ず5組とも一致する筈です。
ですから、多くとも合計4回で判明し5回目で5組一致します。
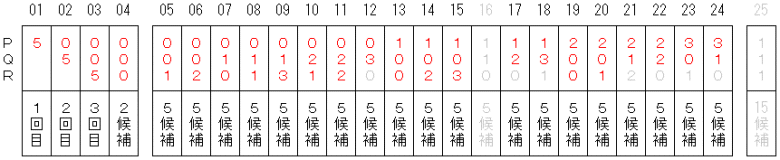
ケース05〜ケース24の時(ケース16は除く)は、奥さん達の並び方の候補はそれぞれ5個ずつしかありません。
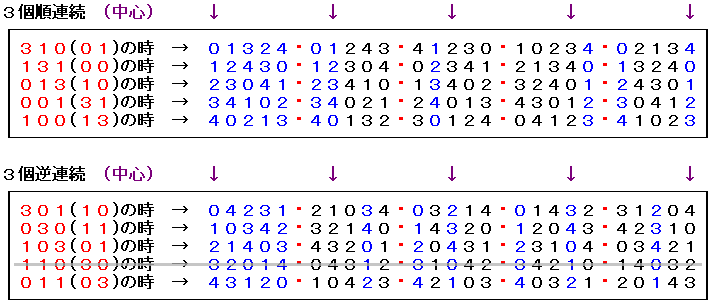
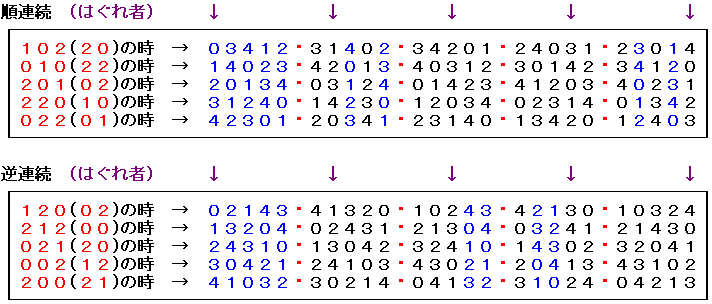
そこで、1番左にある候補の並びで試行します。
(上の図で、青色で示したのが一致箇所)
この時、S組が一致したものとします。
S=5なら、4(3)回で終了です。
S≠5なら、いずれの場合もそれぞれ2個ずつの候補のある2通りの一致組数になります。
得た一致組数の2個の候補を順に試行すれば、多くとも今後2回で必ず5組とも一致する筈です。
ですから、多くとも合計5(4)回で判明し6(5)回目で5組一致します。
P=Q=1の時、奥さん達の並び方の候補は以下の20個です。
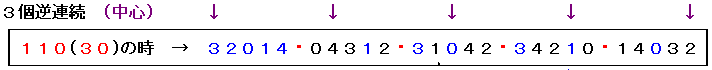

一定歩幅には歩幅1〜歩幅4がありますが、歩幅1は既に示した ケース01〜ケース04 です。
歩幅2〜歩幅4は ケース25 [111(11)] です。
(ただし、歩幅1は連続、歩幅2は1つおき、歩幅3は2つおき、歩幅4は3つおきの意味)
また、この20通りの一定歩幅の並び方には、お互いに次の2つの性質があります。
歩幅の違う並び同士を重ねると、必ず1箇所で一致して4箇所で一致しない。
歩幅の同じ並び同士を重ねると、5箇所とも一致するか5箇所とも一致しない。
そこで、一致組数が1,1,0(ケース16)の時の1番左にある候補の並びで試行します。
(上の図で、青色で示したのが一致箇所)
すると、それぞれの一致組数の候補は以下の通りです。

3組一致なら候補は1個ですから3回で判明し4回目で5組一致します。

(上の図で、青色で示したのが一致箇所)
すると、いずれの場合もそれぞれ2個ずつの候補のある3通りの一致組数になります。
得た一致組数の2個の候補を順に試行すれば、多くとも今後2回で必ず5組とも一致する筈です。
ですから、多くとも合計5回で判明し6回目で5組一致します。