『関数電卓』解答

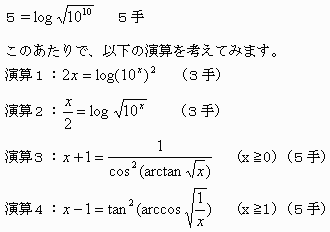
◆東京都　千葉　英伸　さんからの解答。

【問題１】

１＝１０0・・１手
２＝log(１０1)2・・４手
３＝tan2(arccos(cos2(arctan 1)))・・７手
４＝２2・・５手
　

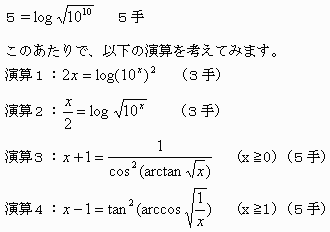
演算１、２はlogの底が10なので、右辺を単純に計算すれば明らかでしょう。

演算３は sin2a+cos2a=1 の両辺をcos2aで割れば、

tan2a+1= １
―――――
cos2a

ここで、 x=tan2aとおいてaを消去すれば得られます。

演算４は演算３の右辺をyとおいてxを消去すれば得られます。

あとは、これらを組み合わせて用いれば、

６＝２×３・・１０手
７＝８−１・・１３手
８＝２×４・・８手
９＝１０−１・・７手
１０＝１０1・・２手
１１＝１０＋１・・７手
１２＝１１＋１・・１２手
１３＝１２＋１・・１７手
１４＝１５−１・・１６手
１５＝１６−１・・１１手
１６＝(２2)2・・６手
１７＝１６＋１・・１１手
１８＝２×９・・１０手
１９＝２０−１・・１０手
２０＝２×１０・・５手

【問題２】

０に対して、問題１の演算３を繰り返し用いることによって、任意の自然数をつくることができます。

【問題３】

任意の自然数ｎに対して、以下の演算で−nを得ることができます。

log １
―――
１０n		＝−ｎ　（３手）

【問題４】

次の命題を考えてみます。

ｎを２以上の自然数とする。
１≦ｍ＜ｎを満たす任意の自然数ｍについて、
関数電卓で ｍ
―――
ｎ		を作ることができる

この命題が証明できれば、 ｍ
―――
ｎ		に対して、
問題１の演算３を必要なだけ、および、問題３の負の演算を用いることによって、ｎを分母にもつ整数でない有理数はすべて作ることができます。
また、整数の場合はすでに問題３で証明済みです。

では、この命題を証明してみましょう。
帰納法で証明します。

まず、ｎ＝２のときは、問題１の演算２によって
１
―――
２		を作ることができます。

次に、ｎ−１までこの命題が正しいとします。
１≦ｋ＜ｎなるｋについて、ｎ−ｋを分母にもつ有理数はすべて作ることができるので、
関数電卓で ｋ
―――
ｎ−ｋ		はすでに作れることがわかっています。

これに問題１の演算３をほどこして（１を加えて）逆数をとれば、
ｎ−ｋ
―――
ｎ		＝ ｍ
―――
ｎ
（１≦ｍ＜ｎ）が得られます。

よって、すべての有理数を作ることができます。

【コメント】

３を作るのにずいぶん手数がかかります。
もっと簡単に作る方法があるかもしれません。
もちろん他の数についても最小手数かどうかは、はなはだ疑問です。

あと、なるべく短い手数で３ｘを作る方法はないものでしょうか？

　『関数電卓』へ

　数学の部屋へもどる