◆愛知県 芋 さんからの解答
{xi}と{yi}に関し全てのn次以下の関数fで
{Σf(xi)-f(yi)}=0という恒等式が成立するとき、
全てのn+1次の関数gと任意の数pにおいて
{Σg(xi)-g(xi+p)-g(yi)+g(yi+p)}=0が成立する。
証明は展開整理して係数を比べるだけにしては、タイピングが面倒なので省略……本当はいけない。[1]
さてまず0次の関数fでは、任意のp, qにおいてf(p)=f(p+q)が成立する。
1次は同様に
f(p)+f(p+q+r)=f(p+q)+f(p+r)、
2次も同様に
f(p)+f(p+q+r)+f(p+q+s)+f(p+r+s)=f(p+q)+f(p+r)+f(p+s)+f(p+q+r+s)
[1]より3次以上も同様に求められる。[2]
具体的に3次以上を求めると
Σf(Σi∈A xi) = Σf(Σj∈¬A xj)、
ここで{i∈A}の元は偶数個、{j∈¬A}の元は奇数個とし、
また全ての{xi}と{xi}の和集合の元は高々2n個で良い、ここでnはfの次数とする。
一般式の記述としては恐らくこれでよいだろう。[3]
さて[2]で(p,q,r,s)=(1,20,21,22)とおくと問題1、問題2の式となる。
ここで本質的に異なるp,q,r,sの組は無い。
1〜8の2進数との比較からこれ以外にないことが理解できる。
ちなみに[3]でn=3,{xi} = {1,20,21,22,23}とおけば
1,4,6,7,10,11,13,16 = 2,3,5,8,9,12,14,15
となる。
タイプが面倒なので説明の省略し過ぎではあるが、何を意味しているかは理解されると思う。
感想
解答の言語が数学になっていなくて申し訳ありません。
証明もかなり省略していますし。
ただ丁寧に穴をふさいでいくと分量が多くなってしまいそうだったので。
もし、それこそが数学の力だ、と突っ込まれたらどうしたらいいのでしょうか。ううむ。
◆東京都 ぽこぺん さんからの解答。
【定義1】
0 〜 2n-1 の 2n 個の整数を 2 進表示したとき,
数字 1 を偶数個含む整数の集合を An,奇数個含む整数の集合を Bn とする。
【定義2】
多項式 f(x) と定数 a,h に対して
fi = f(a+ih) (i = 0,1,…,2n-1)
と書く。
【問題3の解答】
任意の自然数 n,任意の (n-1) 次式 f(x) に対して次の式が成立する。
| Σ i∈An |
fi = | Σ i∈Bn |
fi (*) |
【補題】
任意の自然数 n に対して次の式が成立する。
{i+j | i≠j, i∈An, j∈An} = {i+j | i≠j, i∈Bn, j∈Bn} (**)
【補題の証明】
n に関する数学的帰納法で証明する。
[1] n = 1 のとき,
A1 = {0}
B1 = {1}
であるから,
{i+j | i≠j, i∈A1, j∈A1} = {i+j | i≠j, i∈B1, j∈B1} = φ
[2] ある n に対して(**)が成立していると仮定する。このとき,
An+1 = {2a | a∈An} ∪ {2b + 1 | b∈Bn}
Bn+1 = {2a + 1 | a∈An} ∪ {2b | b∈Bn}
と書けるから,
{i+j | i≠j, i∈An+1, j∈An+1}
= {2a + 2b + 1 | a∈An, b∈Bn} ∪ {2a + 2a' | a≠a', a∈An, a'∈An} ∪ {2b + 2b' + 2 | b≠b', b∈Bn, b'∈Bn}
{i+j | i≠j, i∈Bn+1, j∈Bn+1}
= {2a + 2b + 1 | a∈An, b∈Bn} ∪ {2a + 2a' + 2 | a≠a', a∈An, a'∈An} ∪ {2b + 2b' | b≠b', b∈Bn, b'∈Bn}
となるが,帰納法の仮定から
{2a + 2a' | a≠a', a∈An, a'∈An} = {2b + 2b' | b≠b', b∈Bn, b'∈Bn}
{2a + 2a' + 2 | a≠a', a∈An, a'∈An} = {2b + 2b' + 2 | b≠b', b∈Bn, b'∈Bn}
が成立しているので,
{i+j | i≠j, i∈An+1, j∈An+1} = {i+j | i≠j, i∈Bn+1, j∈Bn+1}
となる。■
【(*)の証明】
n に関する数学的帰納法で証明する。
[1] n = 1 のとき,f(x) は定数(0 次式)であるから,
f(a) = f(a+h)
すなわち
f0 = f1
が成立する。
[2] 任意の (n+1) 次式 F(x) に対し,任意の定数 a,h に対して,
F(a+(i+1)h) - F(a+ih) = f(a+ih)
となる n 次式 f(x) が存在することは明らかである。
ここで,ある自然数 n に対して(*)が成立すると仮定する。そのとき,
| 2n-1 Σ j=0 |
Σ i∈An |
fi+j = |
2n-1 Σ j=0 |
Σ i∈Bn |
fi+j |
が成立するから,
| Σ j∈An |
Σ i∈An |
fi+j + | Σ j∈Bn |
Σ i∈An |
fi+j = | Σ j∈An |
Σ i∈Bn |
fi+j + | Σ j∈Bn |
Σ i∈Bn |
fi+j |
| Σ j∈An |
Σ i∈An |
fi+j = | Σ j∈Bn |
Σ i∈Bn |
fi+j |
が成立する。ここで,両辺はそれぞれ
| Σ j∈An |
Σ i∈An |
fi+j = | Σ i∈An |
f2i + | Σ [i∈An, j∈An, i≠j] | fi+j |
| Σ j∈Bn |
Σ i∈Bn |
fi+j = | Σ i∈Bn |
f2i + | Σ [i∈Bn, j∈Bn, i≠j] | fi+j |
| Σ i∈An |
f2i = | Σ i∈Bn |
f2i |
となるから,
| Σ i∈An |
{F2i+1 - F2i} = | Σ i∈Bn |
{F2i+1 - F2i} |
すなわち,
| Σ i∈An |
F2i + | Σ i∈Bn |
F2i+1 = | Σ i∈Bn |
F2i + | Σ i∈An |
F2i+1 |
が成立するが,両辺をそれぞれまとめて
| Σ i∈An+1 |
Fi = | Σ i∈Bn+1 |
Fi |
を得る。■
◆北海道 小西 さんからの解答
fn(x)をxのn次多項式とする。
一般に任意の等差数列の連続する2n個の項を
| 2n-1 Σ i=1 |
fn-1(Xi) = | 2n-1 Σ j=1 |
fn-1(Yj) (1) |
を満たすようなXとYに分割できることを示すことで、問題1〜3の解答としたい。
ただし、分割の存在については証明できたが、分割の一意性については未解決である。
分割の存在の証明
まず例としてn=4の場合について述べる。
等差数列の一般項を
ap = a + (p - 1)d
とする。
第p項から連続する24=16個の項ap+q(q = 0, 1, …, 15)について
f3(x)に代入すると、
ap+qがqの1次多項式、f3(x)がxの3次多項式であるから、
f3(ap+q)はqの3次多項式となる。
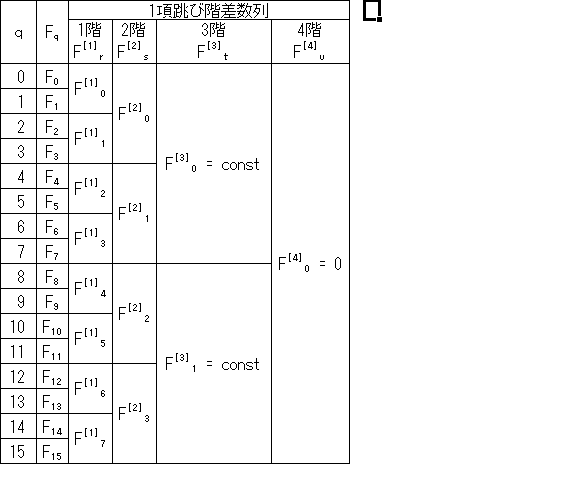
ここで、f3(ap+q)を数列Fqとし、F2r+1とF2rの階差を取り、
F[1]r = F2r+1 - F2r (r = 0, 1, …, 7)
とする。
以下、このような階差数列を1項跳び階差数列と呼ぶことにする。
([ ]は階数を表す)
元の数列がN次多項式の場合、M階1項跳び階差数列の次数は
通常のM階階差数列と同様にMAX(N-M, 0)次になる。(証明略)
従って、Fqの1階1項跳び階差数列F[1]rは2次、
2階1項跳び階差数列F[2]sは1次、
3階1項跳び階差数列F[3]tは定数(≠0)、
4階1項跳び階差数列F[4]uは0となる。
表にまとめると次のようになる。

この表の各セルは左隣の2セルの差(下 - 上)であるから、
いくつかのセルの符号を反転すれば、各セルが左隣の2セルの和となるようにできる。
例えば
F[4]0 = F[3]1 - F[3]0 = F[3]1 + (-F[3]0)
であるから、F[3]0のセルの符号を反転すればよく、さらに
-F[3]0 = -(F[2]1 - F[2]0) = -F[2]1 + F[2]0
であるから、F[2]1のセルの符号を反転すればよい。
この操作を最右列から左に向かって繰り返すと以下のようになる。
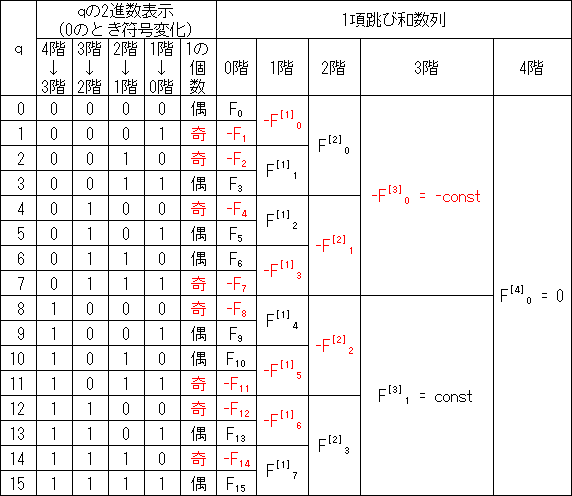
このとき上記の操作手順から、m階の列の符号がm+1階の列の符号と同じかどうかが、
qを2進数表示したときのmビット目(最右桁を0ビット目として)が1かどうかで決まることは明らかである。
従って、最終的に0階の列の符号が変わるかどうかは、qを2進数表示したときの1の個数(または0の個数)で決まる。
このようにして得られた表の各セルは左隣の2セルの和であるから、
F0-F1-F2+F3-F4+F5+F6-F7-F8+F9+F10-F11+F12-F13-F14+F15=0つまり
F0+F3+F5+F6+F9+F10+F12+F15=F1+F2+F4+F7+F8+F11+F13+F14となる。
すなわち、第p項から連続する24=16個の項ap+q(q = 0, 1, …, 15)を
X = {Xi | ap+0, ap+3, ap+5, ap+6, ap+9, ap+10, ap+12, ap+15}
Y = {Yi | ap+1, ap+2, ap+4, ap+7, ap+8, ap+11, ap+13, ap+14}
と分割すれば(1)を満たす。一般のnの場合も上記が適用できるのは自明であるので、任意の等差数列の連続する2n個の項について(1)を満たすX, Yへの分割が存在する。
なお、問題1はn = 2, a = 1, d = 1, p = 1、
問題2はn = 3, a = 1, d = 1, p = 1に相当する。
◆出題者のコメント。
この問題は、Tarry-Escott Problemと言いまして
http://member.netease.com/~chin/eslp/TarryPrb.htm
に紹介されております。
様々な結果が知られているようです。
機会があればお調べください。
◆神奈川県 ヒロ さんからの解答。
x,y,z,wをそれぞれ1,2,3,4のいずれかの異なる数とします。
ここで、
f(x)+f(y)=f(z)+f(w)
が成り立つためには
(ax+b)+(ay+b)=(az+b)+(aw+b)が成り立つ必要があります。
a=0の場合はどのようなx,y,z,wについても上式は成り立ちます。
a≠0の場合はx+y=z+wが成り立つ必要があります。
このようなx,y,z,wの組み合わせは
(x,y,z,w)=(1,4,2,3),(1,4,3,2),(4,1,2,3),(4,1,3,2)
のみなのでそれ以外だと上式は成り立ちません。