◆東京都 サボテン さんからの解答。
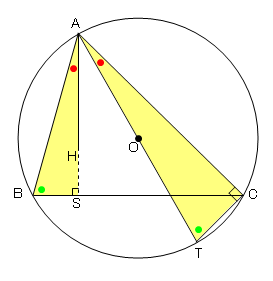
【問題1】
オイラー線が通る頂点をAとする。
この時外心Oは直線AG上にある。
以下Oが辺上にある場合とそれ以外の場合で場合分けする。
1)辺上にある場合
円周角の定理より、これは直角三角形である。
2)辺上にない場合
この場合はBCの垂直二等分線とAからBCに引いた中線が一致する。
よって二等辺三角形である。
【問題2】
AGとBCの交点をPとする。
外接円の半径をRとする。
AB=c,BC=a,AC=bとする。
OG//BCより、PO=csinB/3
△OPBは直角三角形なので、三平方の定理により、
PB2+PO2=BO2
| PB= | a 2 | , BO=Rを代入。 |
| a2 4 |
+ | c2sin2B 9 |
=R2 |
| 正弦定理よりa= | csinA sinC |
,R= | c 2sinC |
を代入し |
| cos2A 4 |
- | sin2Bsin2C 9 |
=0 |
| 1 4 |
- | tanBtanC 2 | +(tanBtanC)2( | 1 4 |
- | 1 9 |
)=0 |
| x=3, | 3 5 |
| ここで、tanBtanC=3 又は | 3 5 | となりますが、 |
| 3 5 | を除去する理由が分かりませんでした。 |
◆東京都の高校生 もやし さんからの解答。
【問題1】
オイラー線が頂点を通る⇔外心Oがその頂点における中線またはその延長上にある
このとき、
[1]Oがその頂点の対辺上にある
[2]Oがその頂点の対辺上にない
の場合が考えられる。
[1]のとき
このとき、Oは辺の中点と一致する。
外心が辺の中点にある三角形は直角三角形であり、その辺は斜辺となる。
[2]のとき
このとき、その頂点の対辺における中線と垂直二等分線が一致する。
中線が辺を垂直に二等分する三角形は二等辺三角形であり、その辺は底辺となる。
以上より、オイラー線が三角形の頂点を通るとき、その三角形が直角三角形または二等辺三角形である。
証明終
【問題2】
〔準備1〕
△ABCの外心をO,垂心をHとするとき、∠BAH=∠OACである。
証明
図1のようにAHの延長とBCとの交点をS,頂点Aを通る直径をATとすると、

△ABSと△ATCにおいて、
∠ABS=∠ATC,∠ASB=∠ACTより、三角形の残りの内角も等しいので、
∠BAS=∠TAC、
すなわち、∠BAH=∠OAC
証明終
〔準備2〕
三角形の垂心はその三角形のオイラー線上にある
証明
図2のように頂点Bを通る直径をBDとし、OからBCに下ろした垂線をOMとする。
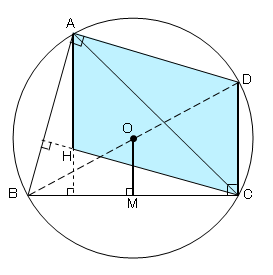
円の中心から弦に下ろした垂線は、その弦を垂直に二等分することから、BM=CM
また、BO=DOより、
△BCDにおいて中点連結定理より、2OM=CD
ここで、AH⊥BC,DC⊥BCより、AH//DC
CH⊥AB,DA⊥ABより、CH//DA
よって、四角形AHCDは平行四辺形なので、AH=CD
故に、AH=2OMより、AH:OM=2:1
図3のように、AとM,OとHをそれぞれ結び、その交点をGとすると、
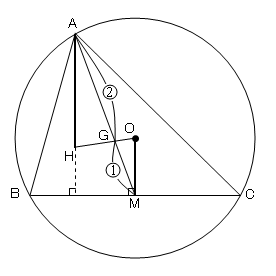
AH⊥BC,OM⊥BCより、AH//OM
従って、△AHG∽△MOGより、
AG:MG=AH:MO=2:1
よって、点Gは△ABCの中線AMを2:1に内分するので、点Gは△ABCの重心である。
従って、3点O,G,Hは同一直線上にあるので、三角形の垂心はその三角形のオイラー線上にある。
証明終
〔本題〕
図4のように、辺BCの中点をMとし、頂点Aから対辺に下ろした垂線をAKとし、AKの延長が再び円Oと交わる点を点Pとする。
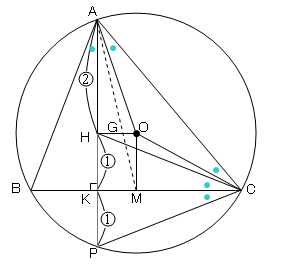
準備1より、∠BCH=∠OCA
OC=OAより、∠OCA=∠OAC
準備1より、∠OAC=∠BAH
円周角の定理より、∠BAH=∠BCP
以上より、∠BCH=∠BCP
また、BK⊥PHより、三角形の内角の二等分線が対辺と直交する三角形はその対辺を底辺とする二等辺三角形なので、
HK=PK
仮定より、OH//BCなので、
AH:HK=AG:GM=2:1
HK=PKより、AK:PK=(2+1):1=3:1なので、
| AK PK |
=3 |
| ところで、tanB= | AK BK |
,tanC= | AK CK |
より、 |
| tanB・tanC= | AK2 BK・CK |
また、方べきの定理より、AK・PK=BK・CK
| 従って、 | AK2 BK・CK |
= | AK PK |
=3 |
∴tanB・tanC=3
証明終