◆宮城県 甘泉法師 さんからの解答
線分ABの長さを2k 点Cと直線ABの距離をnとして
m=√(n2 + u2), u≧0 とすると
| d= | 1 2k |
k ∫ -k | √(n2 + (u+x)2)dx. |
| d-m= | 1 2k |
k ∫ -k | {√(n2 + (u+x)2)-√(n2 + u2)}dx = | f(k) 2k |
| d dk |
f(k) = √(n2 + (u+k)2) - √(n2 + (u-k)2) > 0, f(0)=0 |
よってd-m > 0
◆東京都 ぽこぺん さんからの解答
線分 AB を含む直線 l に点 C から降ろした垂線の足を O とする。
l を x 軸,直線 OC を y 軸とする直交座標系を導入し,
A (a, 0),B (b, 0), C (0, h),かつ a<b とする。
このとき,線分 AB 上の点 P (x, 0) に対して,
線分 CP の長さを f(x) とすると,f(x) は
f(x) = √(x2 + h2)で表せる。
このとき,証明すべきことは
| b ∫ a | f(x) dx > (b-a) f( | a+b 2 | ) …… (*) |
と書ける。
【証明】
(1) 区間 [a, b] で常に次の式が成り立つから,f(x) は下に凸である。
| f ’(x) = | x f(x) |
| f ’’(x) = | h2 {f(x)}3 | > 0 |
(2) 区間 [a, b] で f(x) が下に凸ならば,区間内の点における f(x) の接線は常にf(x) よりも下にある。
| 点( | a+b 2 | , 0) における接線の方程式を y=g(x) とすると, |
| b ∫ a | f(x) dx > | b ∫ a | g(x) dx |
が成り立つ。
これは (*) そのものである。(証明終)
◆出題者のコメント
お二方とも(たぶん)正解だと思います。
同じ問題を友人に見せたときも甘泉法師さんとほぼ同様の解法であったと記憶しています。
やはりこのやり方が自然ですかね。
ただ、僕が最初にこの問題をつくったときに想定した解法はほとんど計算しないやり方でした。
もう少し詳しく言うと、『視覚的にdとmの大小を比較する』って感じでしょうか。
こちらの方法についてもどなたか暇があれば考えてみてください。
結構面白いと思いますよ。
◆愛知県 Y.M.Ojisan さんからの解答
【証明】
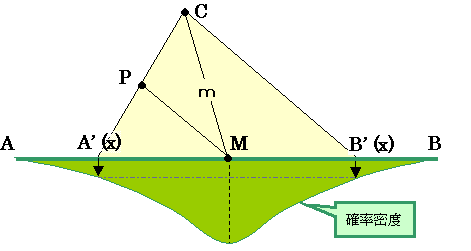
AB上で中点Mから左右に等距離xの点A',B'を考える。
この時A'とB'を選ぶ確率は等しいと考えるのは自然である。(*)
CB'に平行な線分PMを考える。この時三角形のCPMの辺の長さの関係から
m≦(CB'+CA')×0.5である。
ところで、(CB'+CA')×0.5は(*)によりxにおける局所的な期待値d(x)に等しく、
d(x)≧mである。
ここで等号はx=0の時のみであるので、ABの長さが0でないなら、
殆どいたるところd(x)>mである。
よって、左右対称な確率密度分布であれば
d=E[d(x)]>mである。

【PS】
この種の問題を出す側の課題として、確率密度を暗黙にしてよいか今後もこだわりたいと思います。
◆山梨県 Footmark さんからの解答
ABの中点をMとし、Mから等距離にある線分AB上の任意の2点をP,Qとする。
すると、どのような2点P,Qであっても、常に
| PC+QC 2 | >MC(=m) ならば d>m の筈である。 |
Pを通り直線MCに平行な直線をL(P)、
Qを通り直線MCに平行な直線をL(Q)とする。
直線L(P)上でM→Cと同一方向に、PP’=PC となる点P’を、
直線L(Q)上でM→Cと同一方向に、QQ’=QC となる点Q’を、
それぞれとり、直線P’Q’と直線MCの交点をM’とする。
すると、明らかに
| PC+QC 2 | = | PP’+QQ’ 2 | =MM’である。 |
このとき、△PP’Cと△QQ’Cに着目すると、
△PP’CはPP’=PCの二等辺三角形であり、
△QQ’CはQQ’=QCの二等辺三角形である。
| それゆえ、∠PP’C< | π 2 | かつ ∠QQ’C< | π 2 | なので |
すると、PP’とQQ’は平行ゆえ、明らかに3点P’,C,Q’は1直線上になく、CはM’よりMに近い。
つまり、MM’>MC(=m)
| 即ち | PC+QC 2 | >MC(=m) である。 |
よって、d>m である。