◆大阪府 CHECK さんからの解答。
【問題1】
1回の反射で返ってくるためには打ちだした点から進行方向に垂直な面に当たるしかない。
よって、軌道は円の直径部分を往復。
【問題2】
2回の反射で返ってくるとき軌道は円に内接する三角形を描くしかない。
また、ある一点から打ち出された球が跳ね返ったとき、その軌道が作り出す角をθとすれば必ずその後の反射はみなその角度で反射することになる。
(∵連続した反射点と円の中心を結ぶと二等辺三角形が出来る)
よって、1回目の反射、2回目の反射の角度は等しく、それが打ち出された点に来たときの角度も等しい。
よって、軌道は円に内接する正三角形であり、戻ってきた後も再び同じ軌道をたどる。
【問題3】
問題2と同様に考えると、軌道は円に内接する正方形であり、戻ってきた後も再び同じ軌道をたどる。
【問題4】
問題2と同様に考えると、4回の反射で返ってくるとき軌道は円に内接する正五角形もしくは正☆型であり、戻ってきたあとも同じ軌道をたどる。
【ちょっと感想】
問題4はこの2通り以外は考えられないと思うんですが、戻ってきた後の軌道が違うことってあるんでしょうか?
いかなる角度で打ち出したにせよ、僕が問題2で示した「常に反射する角度は同じであること」、を考えればあり得ないとは思うんですが・・・・・・。
◆東京都 鳳 奥人 さんからの解答。
【問題1】
出発点から、円卓の中心に向かって玉をうてば、「ちょうど正反対の位置」に当たって、もとの出発点にかえってくる。
軌道は「出発点と円卓の中心を結ぶ線上を、円卓内で往復する」もの。
【問題2】
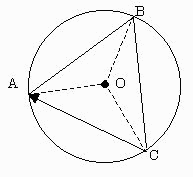
下図の、A→B→C→Aという軌道になる。
(Aは出発点、Oは円卓の中心)

このとき、OB=OCだから∠OBC=∠OCB
また、問題の条件より
∠OBA=∠OBC、∠OAC=∠OCA
つまり
∠OAB=∠OAC=∠OBA=∠OBC=∠OCA=∠OCB(=kとする)
これより、∠ABC=∠ACB=∠BCA=2k
したがって、△ABCは正三角形。
つまり、軌道は「頂点の一つが出発点となるように円に内接する正三角形を設定すると、その正三角形の三辺が軌道となる」。
また、∠OAC=∠OABであるから、戻った後やはり同じ軌道をたどってゆくことになる。
【問題3】
問題2と同様に考えれば、
「頂点の一つが出発点となるように、円に内接する正方形を設定すると、その正方形の四辺が軌道となる」。
戻ってきたあとはやはり同じ軌道をたどってゆく。
【問題4】
やはり同じ考え方をすれば
「頂点の一つが出発点となるように、円に内接する正五角形を設定すると、その正五角形の五辺が軌道となる」。
戻ってきたあとはやはり同じ軌道をたどってゆく。
以上、解答終わり。
・・・と思ったら、よく考えると下図みたいなパターンもありますね。
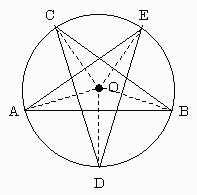
軌道はA→B→C→D→E→Aです。
(Aは出発点、Oは円卓の中心)
ここで、△OAB、△OBC、△OCD、△ODE、△OEAはすべて合同な二等辺三角形だから
(底角がすべて等しいので頂角もやはり等しく、また頂角をはさむ二辺の長さはどれも半径に等しいから)、
∠AOB=∠BOC=∠COD=∠DOE=∠EOA
したがって、
∠AOD(=360°−∠DOE−∠EOA)
=∠DOB(=360°−∠BOC−∠COD)
=∠BOE(=360°−∠EOA−∠AOB)
=∠EOC(=360°−∠COD−∠DOE)
=∠COA(=360°−∠AOB−∠BOC)
つまり、五角形ADBECは正五角形になり、またこの軌道はこの正五角形の五本の対角線となる。
だから「頂点の一つが出発点となるように、円に内接する正五角形を設定すると、その正五角形の五本の対角線が軌道となる」 ・・・といったところでしょうか。
鏡面を円形に組んで、そこに直線状の光線を当ててやるという実験をしてみれば、おおよその推測はできますよね。
夏休みの自由研究テーマにつかえるかもしれません。