乮媴偺拞怱偐傜偦偺侾曈偺嵟抁偵偁偨傞拞揰傑偱偺嫍棧偱偝偊
俁
仧搰崻導偺拞妛峑俁擭惗丂巟棧柵楐 偝傫偐傜偺夝摎丅
亂栤戣侾亅侾亃
俻俼偺挿偝偑俹偺埵抲偵傛傜偢堦掕偱偁傞帪偲偼丄揰P偑AB偺拞怱偵棃偨偲偒偱偡丅
側偺偱丄仮APQ=仮QPR=仮RPB=惓嶰妏宍偱偡丅
亪佢倶亖60亱
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣俀亃
惓嶰妏悕偺偡傋偰偺曈偺撪偱丄捈宎偲側偭偨侾曈偼偡傋偰媴撪偵偁傝丄捈宎偲楢寢偟側偄桞堦偺侾曈偼偡傋偰媴奜偵偁傞丅
乮媴偺拞怱偐傜偦偺侾曈偺嵟抁偵偁偨傞拞揰傑偱偺嫍棧偱偝偊
俁![]() cm偱柧傜偐偵俁
cm偱柧傜偐偵俁![]() 亜俁乯
亜俁乯
偲偙傠偑懠偺係曈偼恾偺傛偆偵媴柺傪娧偒丄係曈偲傕偪傚偆偳敿暘偢偮偑媴偺撪偲奜偵偁傞丅
偦傟屘丄恾偱愒偄屖偱帵偟偨傛偆偵丄係偮偺暿乆側暯柺忋偵偦傟偧傟侾杮偢偮偺岎慄偑偁傞丅
偳偺岎慄傕丄媴偺拞怱偐傜奐偒妏搙俇侽亱偺俀偮偺敿捈慄偑丄媴柺偲岎嵎偡傞俀揰娫偺媴柺忋偱偺嵟抁宱楬偱偁傞丅
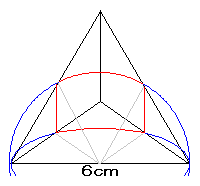
| 傛偭偰丄媮傔傞岎慄偺慡挿亖 | 俇兾 俇 | 倃係亖係兾 |
亂摎偊亃係兾 cm
亂俹丒俽亃
惓嶰妏悕偺曈偱峔惉偝傟偨崪慻傒偺宍偼媴偺撪晹傕奜晹傕摨宍(棫懱揑崌摨)偵側傝柺敀偄偱偡偹丅
仧弌戣幰偺僐儊儞僩
亂栤戣侾亅侾亃
俻俼偺挿偝偑俹偵傛傜偢堦掕偱偁傞帪偲偼丄揰俹偑俙俛偺拞怱偵棃偨偲偒偱偡丅
側偺偱丄佢倶亖俇侽亱
偲偺偙偲偱偡偑丄偙傟偼廫暘忦審偺傒傪帵偝傟偰偄傞偩偗側偺偱丄昁梫忦審傕峫偊偰傒偰偔偩偝偄丅
偦偆偡傞偲惓夝偑尒偊偰偔傞偼偢偱偡丅
亂栤戣俀亃
堦尒惓夝偺傛偆側婥偑偟偨偺偱偡偑丄捈宎偲側傞曈傪娷傑側偄俀偮偺嶰妏宍偲偺岎慄偼偙傟偱惓偟偄偱偟傚偆偐丠
拡偵晜偐側偄偱偟傚偆偐丠
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣俀亃
屖(岎慄)偺敿宎偼俀庬椶偱偟偨丅
嵍偑捈宎傪娷傓俀柺偱偺岎慄丄塃偑懠偺俀柺偱偺岎慄偱偡丅

捈宎傪娷傓俀柺偱偺屖(岎慄)偺敿宎偼丄媴偺拞怱傪娷傓暯柺忋偵偁傞偺偱俁cm丅
| 偦偙偱偺屖(岎慄)偺拞怱妏偼 | 兾 俁 | 丅 |
懠偺俀柺偱偺屖(岎慄)偺敿宎偼丄
侾曈俁cm偺惓嶰妏宍偺奜愙墌偺敿宎偵側傞偺偱![]() cm丅
cm丅
| 偦偙偱偺屖(岎慄)偺拞怱妏偼 | 俀兾 俁 | 丅 |
傛偭偰丄
丂媮傔傞岎慄偺慡挿
| 亖俀* | 俇兾 俇 | 亄俀* | 俀 俁 |
| 亖 | (俇亄係 俁 |
| 亂摎偊亃丂 | (俇亄係 俁 | cm |
亂栤戣俁亅侾亃
傑偢丄捈宎傪曈偵傕偮柺偼丄掙柺偺惓曽宍偲侾懁柺偺惓嶰妏宍偺俀柺丅
掙柺偺惓曽宍偱偺屖(岎慄)傕侾懁柺偺惓嶰妏宍偱偺屖(岎慄)傕敿宎偼嫟偵俁cm丅
乮偳偪傜傕媴偺拞怱傪娷傓暯柺忋側偺偱偙傟偼柧傜偐乯
屖(岎慄)偺拞怱妏偼丄掙柺偺惓曽宍偱偼 兾丄
| 侾懁柺偺惓嶰妏宍偱偼亂栤戣俀亃偲摨條偵 | 兾 俁 | 丅 |
師偵丄捈宎傪曈偵傕偮惓嶰妏宍偲懠偺侾曈傪嫟桳偡傞俀懁柺偺惓嶰妏宍傪峫偊偰傒傞丅
屖(岎慄)偺敿宎偑偄偔傜偐偼晄柧偩偑丄尫偺挿偝偼俁cm丅
偦偙偱丄偦偺愗抐柺偺墌偺敿宎傪媮傔偰傒傞丅
奺懁柺偑掙柺偵挘傞孹偒偼丄
惓嶰妏宍偺掙曈偺拞揰偐傜掙柺偺拞怱傑偱俁cm恑傫偱
惓巐妏悕偺崅偝俁![]() cm偲側傞偺偱
cm偲側傞偺偱![]() 丅
丅
偦傟屘丄尨揰(侽丆侽)偐傜師偺俀幃偺岎揰(倶丆倷)傑偱偺嫍棧偑愗抐柺偺墌偺捈宎偲側傞丅
倷亖![]() 倶
倶
(倶亅俁)2亄倷2亖俁2
偙傟傪夝偔偲丄倶亖俀丆倷亖俀![]() 傪摼傞丅
傪摼傞丅
傛偭偰丄
| 愗抐柺偺墌偺敿宎亖 | 併(倶2亄倷2) 俀 |
亖 |
敿宎![]() cm偺墌偱
cm偺墌偱
| 尫偺挿偝偑俁cm側偺偱丄拞怱妏偼 | 俀兾 俁 | 丅 |
傑偨丄捈宎傪曈偵傕偮惓嶰妏宍偲偳偺曈傕嫟桳偟側偄侾懁柺偺惓嶰妏宍傑偱偼柧傜偐偵媴偼媦偽側偄丅
埲忋傛傝丄
丂媮傔傞岎慄偺慡挿
| 亖 | 俇兾 俀 | 亄 | 俇兾 俇 | 亄俀* | 俀 俁 |
| 亖 | (侾俀亄係 俁 |
| 亂摎偊亃丂 | (侾俀亄係 俁 | cm |
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣俁亅俀亃
捈宎傪曈偵帩偮俀偮惓嶰妏宍偱偺岎慄偼丄亂栤戣俀亃摨條偵
| 嫟偵敿宎俁噋偺墌偺拞怱妏 | 俀兾 俇 | 偺屖偲側傞丅 |
懠偺俀偮偺惓嶰妏宍偱偺岎慄偼丄亂栤戣俁亅侾亃摨條偵
| 嫟偵敿宎 |
俀兾 俁 | 偺屖偲側傞丅 |
傑偨丄掙柺偺惓曽宍偱偺岎慄偼丄俀曈偑俁噋偺捈妏擇摍曈嶰妏宍偺掙曈偑奜愙墌偺尫偲側傞偲偒偺屖偱偁傞丅
| 傛偭偰丄敿宎 | 俁 俀 |
噋偺墌偺拞怱妏 | 俀兾 俀 | 偺屖偲側傞丅 |
埲忋傛傝丄
媮傔傞岎慄偺慡挿
| 亖俀* | 俇兾 俇 |
亄俀* | 俀 俁 |
亄 | 俁 俀 |
| 亖 | (侾俀亄俋 俇 |
| 亂摎偊亃丂 | (侾俀亄俋 俇 |
噋 |
仧弌戣幰偺僐儊儞僩丅
惓夝偱偡丅
偨偩亂栤戣俁亅侾亃偑崅峑惗埲忋偺恖偺夝偒曽偐側丠偲巚偄傑偟偨丅
拞妛惗儗儀儖偱傕夝偗傞傛偄夝摎偼側偄傕偺偱偡偐偹偊丠
亂栤戣俁亅俀亃偺椶帡栤戣偑暯惉13擭偺戝嶃偺朸巹棫崅峑偺擖帋栤戣偵偩偝傟偨傛偆偱偡丅
寢峔擄偟偐偭偨偺偱偼側偄偱偟傚偆偐丠
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣俁亅侾亃
墌偺曽掱幃傪巊梡偟側偄拞妛惗僶乕僕儑儞偺偮傕傝偱偡丅丱丱丟
傑偢丄捈宎AB傪曈偵傕偮柺偼丄惓曽宍ABCD偲惓嶰妏宍VAB偺俀柺丅
惓曽宍ABCD偱偺屖(岎慄)傕惓嶰妏宍VAB偱偺屖(岎慄)傕敿宎偼嫟偵俁噋丅
乮偳偪傜傕媴偺拞怱傪娷傓暯柺忋側偺偱偙傟偼柧傜偐乯
屖(岎慄)偺拞怱妏偼丄惓曽宍ABCD偱偼 兾丄
| 惓嶰妏宍VAB偱偼亂栤戣俀亃偲摨條偵 | 兾 俁 | 丅 |
師偵丄惓嶰妏宍VAB偺懁柺偵偁傞俀屄偺惓嶰妏宍VDA偲VBC傪峫偊偰傒傞丅
偳偪傜偺惓嶰妏宍偵偍偄偰傕丄屖(岎慄)偺敿宎偼晄柧偩偑尫偺挿偝偼俁噋偱偁傞丅
傑偨丄奺惓嶰妏宍偑掙柺偵挘傞孹偒偼丄
惓嶰妏宍偺掙曈偺拞揰偐傜掙柺偺拞怱傑偱俁噋恑傫偱
惓巐妏悕偺崅偝俁![]() 噋偲側傞偺偱
噋偲側傞偺偱![]() 丅
丅
偦偙偱丄惓嶰妏宍VDA傪娷傓柍尷偵戝偒偄暯柺偱媴傪愗抐偡傞傕偺偲偡傞丅
偡傞偲丄媴偺愗抐柺偼墌偵側傝丄媮傔傞岎慄偼偦偺墌廃偺侾晹偺敜偱偁傞丅
愗抐柺偱偁傞墌偺捈宎偼丄嵟戝墌(媴偺拞怱傪娷傓墌)偲偦傟偵捈岎偡傞愗抐柺偲偺俀岎揰偺嫍棧偱偁傞丅
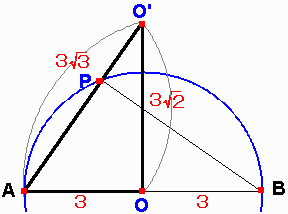
恾偱帵偡偲丄愗抐柺偺墌偺捈宎偼柧傜偐偵PA偲側傞丅
偲偙傠偱丄AO亖俁噋丄OO乫亖俁![]() 噋 側偺偱丄
噋 側偺偱丄
僺僞僑儔僗偺掕棟傛傝 AO乫亖俁![]() 噋 丅
噋 丅
傑偨丄仮PAB偲仮OAO乫偲偼憡帡側偺偱
| PA 俇 | 亖 | 俁 俁 |
屘偵 俹俙亖俀![]() 噋丅
噋丅
傛偭偰丄愗抐柺偺墌偺敿宎亖![]() 噋丅
噋丅
敿宎![]() 噋偺墌偱尫偺挿偝偑俁噋側偺偱丄
噋偺墌偱尫偺挿偝偑俁噋側偺偱丄
| 拞怱妏偼 | 俀兾 俁 | 丅 |
偙偺偙偲偼惓嶰妏宍VBC偺屖(岎慄)偵偍偄偰傕摨條偱偁傞丅
傑偨丄惓嶰妏宍VCD傑偱偼柧傜偐偵媴偼媦偽側偄丅
埲忋傛傝丄
媮傔傞岎慄偺慡挿
| 亖 | 俇兾 俀 |
亄 | 俇兾 俇 |
亄俀* | 俀 俁 |
| 亖 | (侾俀亄係 俁 |
| 亂摎偊亃丂 | (侾俀亄係 俁 | cm |
仧搶嫗搒丂偐偊傞 偝傫偐傜偺夝摎丅
亂栤戣侾亅侾亃
俙俛偺拞揰乮偡側傢偪墌偺拞怱乯傪俷丄俙俛偵懳偟偰俼偺慄懳徧偲側傞揰傪俼乫偲偡傞丅
偙偺偲偒丄佢俷俹俻亖佢俛俹俼乫亖倶傛傝丄俹偼俼俼乫忋偵偁傞丅
佢俷俻俹亖佢俷俼乫俹
乮佹仮俷俻俼乫偼俷俻亖俷俼乫亖俁偺擇摍曈嶰妏宍乯
亖佢俷俼俹
乮佹俼偲俼乫偼俙俛偵懳偟偰慄懳徧乯
傛偭偰丄墌廃妏掕棟偺媡傛傝丄巐揰俷丄俻丄俼丄俹偼摨堦墌廃忋偺揰丅
佢俻俷俼亖佢俻俹俼乮佹墌廃妏掕棟乯亖兾亅俀倶
| 俻俼亖俁丒俀sin乮 | 兾亅俀倶 俀 | 乯 |
亂栤戣侾亅俀亃
梋尫掕棟傛傝丄
俻俼2亖俹俻2亄俹俼2亅俀俹俻丒俹俼cos乮兾亅俀倶乯
俹俻2亄俹俼2偑堦掕
佁
俀俹俻丒俹俼cos乮兾亅俀倶乯偑堦掕
乮佹亂栤戣侾亅侾亃傛傝丄俻俼2偼忢偵堦掕乯
偙傟偑俹偺埵抲偵偐偐傢傜偢堦掕偵側傞偺偱丄
cos乮兾亅俀倶乯亖侽
佁
| 倶亖 | 兾 係 | 乮佹侽亝倶亝 | 兾 俀 | 乯 |
| 仮俷俻俼偼佢俻俷俼亖佢俼偺捈妏嶰妏宍傛傝丄俷俵亖 | 俁 |
| 俵偺抂揰偑乮亇 | 俁 俀 | 丆 | 俁 俀 | 乯偱偁傞偙偲偵拲堄偟偰丄 |
| 俵偺婳愓偺挿偝亖俀丒 | 俁 |
丒兾丒 | 侾 係 | 亖 | 俁 係 |
兾 |