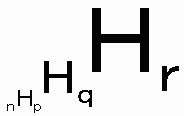
◆愛知県 Y.M.Ojisan さんからの解答。
玉の種類の数=n
1袋の玉数=pより
袋の種類の数:F=n種からp個選ぶ重複組み合わせ nHp
1箱の袋数=qより
箱の種類の数:B=F種からq個選ぶ重複組み合わせ FHq
箱の総数=rより
詰め合わせの種類の数:T=B種からr個選ぶ重複組み合わせ BHr
すなわち
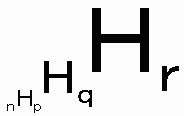
| 注) nHp= | (n+p-1)! p!(n-1)! |
◆出題者のコメント
Y.M.Ojisanさん、解答ありがとうございます。
みごと正解です。
求める組み合わせの数は、1箱の組み合わせの数さえわかれば求めることができます。
何故なら、その数だけ箱の種類はできるので、その数の箱から重複を許してr箱を選ぶ組み合わせです。
1箱の組み合わせの数は、1袋の組み合わせの数さえわかれば求めることができます。
何故なら、その数だけ袋の種類はできるので、その数の袋から重複を許してq袋を選ぶ組み合わせです。
ところで、1袋の組み合わせの数は、明らかにn種類の玉から重複を許してp個を選ぶ組み合わせです。
ですから、示されたように重複組み合わせの重複組み合わせのさらに重複組み合わせになります。
それから、綺麗な画像には劣りますが、答えはタグを使った表示でも可能です。
答え
nHpHqHr=((((n+p-1Cp)+q−1)Cq)+r−1)Cr