◆広島県 清川 育男 さんからの解答。
【問題1−1】
考えやすくするために、仮に終業時間を午後5時とする。
旦那さんが歩いた分早く帰宅することが出来るが、往復で30分早くなっているので、片道では、15分短縮したことになる。
すなわち迎えに行った奥さんは午後4時45分に旦那さんに出会ったことになる。
旦那さんは5時から40分前すなわち4時20分から歩きはじめて4時45分に出会っているので、25分間歩いたことになる。
「もうひとつの算数にチャレンジ」に以前類題が出題されたことがあります。
代数で解こうとするとかなり厄介ですね。
まさに算数という感じです。
【問題1−2】
同じように仮に終業時間を午後5時とする。
現実を無視して奥さんは休むこともなく寝ることもせず24時間運転する。
片道12時間かけて迎えに行って、終業時間の午後5時に会社に着く。
12時間かかって翌朝の午前5時に帰宅して、またすぐに迎えのために家を出るという毎日。
このとき40分前に仕事を終えた旦那さんは、(現実を無視して)テレポーテイションで帰宅出来たとする。
午後4時20分に帰宅したとすれば、いつもの帰宅時間である翌朝の午前5時より、12時間40分早く帰宅出来たことになる。
非現実的ではあるが、12時間40分が限界となる。
旦那さんはテレポーテイションで出社するのでしょうね。
なんのために奥さんは不眠不休で迎えに行くのでしょうか????。
【問題2】
問題1−1のようにスマートな算数的解法がヒラメキません。
自宅からいつも出会う地点までの距離を X(km)とする。
いつも出会う地点から教会までの距離を Z(km)とする。
自宅から教会までの距離を Y(km)とする。
旦那さんの走る速さを M(km/h)とする。
奥さんのいつもの走る速さを F(km/h)とする。
プラスアルファ分の走る速さを α(km/h)とする。
| X+Y+Z F | = | X+Z F | + | Y ― F | = | 2 ― 3 | + | 7 12 | * | M F | = | 2 ― 3 | + | 7 12 | * | 2 | = | 11 6 | (時間) |
M/Fの求め方がヒラメキません。
そこでコツコツ計算しました。
| α= | F+M 7 | , | M ― F | =2 | (M:F=2:1) |
答え 1時間50分
◆出題者の山梨県 Footmark さんからのコメント。
【問題1−1】
代数を知らない小学生にも容易に理解できる鮮やかな解答ですね。
正解です!
おっしゃる通り、まさに算数です。
【問題1−2】
問題の前提により、必ず迎えに来る途中の奧さんの車に乗って帰宅します。
仮に、とんでもなく長距離を光速で歩き、自宅から1mしか進んでない奥さんの車に乗り帰宅したとします。
テレポーテイションなら0秒でしょうが、会社が終了してから1秒後には帰宅したとしても、本当にその時の帰宅時刻が、いつもの帰宅時刻より12時間39分59秒も早くなるんでしょうか?
これを解くと面白い事実が発見できます。
【ヒント】
旦那さんに途中で出会った車は、もし出会っていなければ、その後いつもならどうしたのでしょう?
【問題2】
M/Fが違っているような気がしますが・・!?
【ヒント】
ある時間を未知数として式を立てれば、至って簡明な式になります。
◆広島県 清川 育男 さんからの解答。
【問題1−2】
問題の前提を無視して、勝手な解釈をして申し訳ありません。
「問題の前提により、必ず迎えに来る途中の奧さんの車に乗って帰宅する。」
という条件があれば、
午後5時を終業時間としたとき、仮に40分短縮出来るとすると、午後4時40分に、旦那さんに出会うことになる。
そうなると旦那さんは4時20分に仕事を終えて、20分間車まで歩いたことになる。
旦那さんの歩く速さと車の速さは同じということになる。
旦那さんを車に乗せて20分後の5時に帰宅することになる。
いつもは5時40分に帰宅している。
なぜなら奥さんは午後4時20分に車で自宅を、旦那さんは同じ時刻にしかも車と同じ速さで歩いて会社を出る。
丁度、中間点で4時40分に出会う。
車に乗せて20分後の5時に帰宅する。
したがって、仮定の40分短縮は可能である。
旦那さんは午後4時20分に超高速で自宅の前まで帰って、4時20分に迎えに出た奥さんの車に乗って帰宅。
4時20分1秒。79分59秒。
40分の2倍の短縮に限りなく近づく。
【問題2】
間違えていました。
ヒントに従って方程式を作ればスッキリしましが、Nについての2次方程式を解くことになりました。
算数でも解けるのでしょうか?
旦那さんが1周するのに要する時間をN(時間)とすると、
N=1、F=7α
| M= | 56 5 | α |
M:F=8:5
したがって、奥さんが1周するのに要する時間は1時間36分。
答え 1時間36分
◆出題者のFootmark さんからの解答。
【問題1−1】
帰宅時刻が早くなったのは、明らかに2人が出会った所から会社までの車での往復時間が省略できたためです。
当然、その道のりの片道に要する時間は、省略された時間30分の半分の15分になります。
また、車はいつもの終業時刻には会社に到着する予定でしたので、2人が出会った時刻はいつもの終業時刻の15分前の筈です。
結局、旦那さんはいつもの終業時刻の40分前から15分前までの25分間歩いたことになります。
【答え】 25分
【問題1−2】
旦那さんは、歩き始めた時刻(会社が終わった時刻)以前に奥さんの車に出会うことはあり得ませんし、そのまま会社で待っていても必ずいつもの終業時刻には奥さんの車に出会える筈です。
それに、どのような移動もいかに僅かにしても時間はかかりますから
いつもの終業時刻 > 2人が出会った時刻 > 会社が終わった時刻2人が出会った所から会社までの車での移動時間をm分と仮定すると、2人が出会った時刻はいつもの終業時刻のm分前の筈です。
また、
会社が終わった時刻=いつもの終業時刻ー会社が早く終わった時間(40分)です。
∴いつもの終業時刻 > いつもの終業時刻−m分 > いつもの終業時刻−会社が早く終わった時間(40分)∴0 < m < 会社が早く終わった時間(40)
帰宅時刻がいつもより早くなる時間は、2人が出会った所から会社までの車での往復時間(2m)ですから
0 < 2m < 会社が早く終わった時間の2倍(80)
∴ 0分 < 帰宅時刻がいつもより早くなる時間 < 会社が早く終わった時間の2倍(80分)【答え】
[自宅と会社の距離],[歩く速さ],[車の一定の速さ]が、0より大きいどんな値になろうとも、帰宅時刻がいつもより早くなる時間は、会社が早く終わった時間の2倍(80分)以上になることはありません。
【問題2】
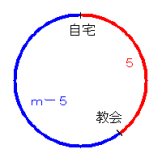
自宅を出発してから35分後には、旦那さんも奥さんも教会の前にいます。
(ただし、旦那さんは青コース、奧さんは赤コース)

今回、奥さんがコース1巡を終了した時、いつもより少なかった時間を m分
(m>5) とすると
| 今回奥さんはコースの | 5 m | の距離を走るのに、 |
| 旦那さんはコースの | m−5 m | の距離を走るのに、 |
それ故
| 奥さんの今回のコース1巡の時間 = 35× | m 5 |
| 旦那さんのコース1巡の時間= 35× | m m−5 |
また、同時に出発した2人ですが、自宅には旦那さんの方が24分先に到着したのですから
| 35× | m 5 | −35× | m m−5 | = 24 |
7m2 − 94m + 120 = 0
(m−12)(7m−10) = 0
| ∴ m = 12 , | 10 7 |
ところが、
| 10 7 | は | 10 7 | > 5 を満たさないため解ではありません。 |
∴ m = 12
それ故、奥さんにとって
いつものコース1巡の時間
= 今回のコース1巡の時間 + いつもより少なかった時間
| = 35× | m 5 | + m |
【答え】 96分(1時間36分)
◆東京都 鳳 奥人 さんからの解答。
【問題1−1】

奥さんの往復走行時間が30分短かった・・・ということになるのですね。
ということは片道で15分の短縮。
つまりAとCの間が15分です。
で、旦那さんが歩いたのはBとCの間ですから、40−15=25で
徒歩時間は25分ということになります。
【問題1−2】
上の図で考えてみましょう。
EとFの差だけが今回は不明、ということになります。
C・F以外の点はすべて固定です。
DF=DC×2ですから、Cが決まればFも自動的に決まります。
だから、ポイントは、Cがどこに来るか・・・ということになると思います。
CがBより前に来ることはない・・・ですよね。
というわけで、CとBが一致した場合が一番早くなる。
このとき、片道40分の短縮だから、帰宅時刻は80分早くなります。
これ以上は早くなりません。
よって早くなる時間は「80分以下」。
・・・と思ったら、CがBと一致するということは
「旦那の終業時刻と奥さんの会社到着が同時」って意味ですよね。
奥さんの走行速度はいつもと一緒だから、これはつまり「AとBが一致」ということになってしまいます。
これはありえないですね。
ということは、CはつねにBの後。
だから「80分早くなる」ことはありません。
ただしB・Cの間隔を限りなくゼロに近づけていくと、早くなる時間も限りなく80分には近づいていきます。
以上より、「早くできる時間の幅は80分未満」。
【問題2】
旦那さんの速度をH、奥さんの普段の速度をW(ともに分速)とすると、 教会到着時刻から奥さんの今日の速度は(40/35)W すなわち(8/7)Wです。
一周分の距離は、教会到着時点で奥さんが走った距離(40W)と
旦那さんが走った距離(35H)を足した
35H+40Wです。
今日の旦那さんが一周にかかった時間は
| 35H+40W H | = | 40W H | +35 |
同じく奥さんは
| (35H+40W)/( | 8 7 | W)= | 245H 8W | +35 |
| だから | 245H 8W | +35=( | 40W H |
+35)+59 |
全体に8HWをかけた上で整理すると
320W2 + 192WH - 245H2= 0
何とか因数分解して(8W-5H)(40W+49H)=0
ここでH>0、W>0なのは明らかですから
| W= | 5 8 |
H |
| というわけで、ふだんの奥さんの速度は | 5 8 |
H |
| 今日の奥さんの速度はこれに | 8 7 |
をかけた | 5 7 |
H |
ここから、普段の奥さんが一周にかかる時間は
| 60H÷ | 5 8 |
H=96(分)です。 |
| ちなみに、今日は60H÷ | 5 7 |
H=84(分)。 |
※因数分解が大変でした。
二次方程式の解の公式なんてのを数年ぶりに記憶の底からひっぱりだしてきました(笑)
◆出題者のコメント。
鳳 奥人 さんへのコメントです。
解答ありがとうございます。
全問ともみごと正解です。
【問題1】の図はとても分り易いため説得力がありますね。