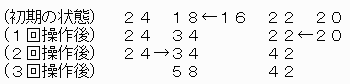
◆山梨県 Footmark さんからの解答。
【問題1】,【問題2】のいずれの場合も、
(3) 最後まで残って水の量が減っている。
ようなことは、条件に従った操作では起き得ません
【問題1】
| x< | 1 3 |
のときは、以下の2通りがあります。 |
(1) 操作の途中で空になって取り除かれる。
(2) 最後まで残って水の量が増えている。
【証明】
仮にビーカーが3個になったときでも、最初xリットルの水が入ったビーカーが最初の状態のままで残ったものとすると、
| x(< | 1 3 |
)リットルが3個のビーカーの水の内で最多であることはあり得ません。 |
最多なら水の総量は1リットルに満たなくなり題意に反します。
ですから、2つのビーカーにするときには、(1)か(2)のいずれかで、
(4) 最後までxリットルの水が入ったままで残る。
ようなことは起き得ません。
以下、(1)や(2)が起こる例を各ビーカーの容量と水の総量を100として示します。
(1)になるケース
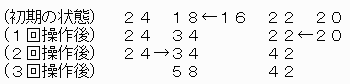
(2)になるケース
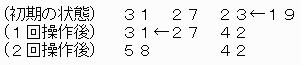
【問題2】
| x> | 2 5 |
のときは、以下の1通りしかありません。 |
(4) 最後までxリットルの水が入ったままで残る。
【証明】
ビーカーがm個のとき、そこで最少である2個のビーカーの水の合計量が、
| 最多であるx(> | 2 5 |
)リットルの水の量以上になったものとします。 |
mの最大値を得るためには最少である2個のビーカーの水の合計量を、できるだけ多くさせる必要があります。
それには、xリットル入りのビーカーは
| x> | 2 5 |
の範囲でxを最少にさせ、 |
| 他のビーカーは残りの水(< | 3 5 |
)を等分させれば良い筈です。 |
| dを正の無限小値とし、x= | 2 5 |
+d とすると、 |
| 2 5 |
+d≦ |
m−1 |
| m≦ | 8−5d 2+5d |
< | 8 2 |
=4 |
∴ m<4
結局ビーカーが4個以上なら、そこで最少である2個のビーカーの水の合計量が
| 最多であるx(> | 2 5 |
)リットルの水の量以上になることはあり得ません。 |
これは、最初ビーカーの数が4個以上なら3個になっても、
| x(> | 2 5 |
)リットルが3個のビーカーの水の内で最多であることを意味します。 |
ですから、
(4) 最後までxリットルの水が入ったままで残る。