右と上にしか行かない場合です。
◆広島県 清川 育男 さんからの解答。
図の蜘蛛のいる頂点から対角にある頂点は3個。
対角にある頂点から直進するのが最短コースとなる。
n個のマスとn個のマスがあるとき対角までの最短コースの経路の数は(n+n)個から同じものをn個とる順列に等しい。
したがって、求める最短経路の個数は、
(2nCn×3)個。
答え 3×2nCn個。
順列組み合わせの問題が多いですね。
「つり銭をなくせ」の問題に似ています。
見方を変えると同じ問題という意味では頭の体操になります。
◆広島県 清川 育男 さんからの解答。
間違っていました。
展開図を考えると、最短コースの経路は2n個とn個のマスのある長方形4つのなかにある。
この長方形の対角にある頂点までの最短経路の個数の問題に還元される。
この経路は同じ(2n+n)個からn個または2n個をとる順列に等しい。
例えば、縦n個のマス、横2n個マスの長方形の場合、左下の頂点からその対角にある頂点までの最短経路は、右に2n個のマス、上にn個のマスを取る組み合わせになる。
また3nCn=3nC2nである。
したがって求める経路の個数は、
| 3nCn×4= | (3n)!×4 ――――――――――― (2n)!×n! |
【出題者のフェイクさんからのコメント】
展開図を考えて、2n×nの長方形に問題を還元するという考え方はいいです。
でも本当にかける数は4で良いのでしょうか?
また、本当に重複はないのでしょうか?
その辺を調べるためにも2×2×2や3×3×3の桝目がついている立方体で考えてみることをお勧めします。
感想:
蜘蛛が描いてある図に騙されてはいけません。
見えないところにも道があるのです。
◆広島県 清川 育男 さんからの解答。
また間違えていました。
三度目の正直になるといいのですが。
ご指摘のように2n個のマス、n個のマスの長方形が6個あります。
またn個のマス、n個のマスの正方形が6個重複します。
したがって求める最短経路の個数は、
(3nCn−2nCn)×6個となります。
◆石川県 Takashi さんからの解答。
正面から右側面を見たときの経路は、
2nCn
これが6面あるので6倍にして、重複経路はnに関係なく6通り。
よって、
6×2nCn−6
これくらいかな?
◆石川県 青木からの解答。
実はこの問題は解答をお聞きしていないので、私も考えてみました。
ただし自信はないです。
間違っていたら教えてください。
最初にa×bの長方形について考えると、最短距離で進む方法は

右と上にしか行かない場合です。
したがって、(a+b)回のうち、上へa回行けばよいのだから、場合の数は
| a+bCa= | (a+b)! ―――――― a!b! |
a×b×cの直方体についても同様に考えて、
| a+b+cCc×a+bCb= | (a+b+c)! ―――――――― a!b!c! |
この問題では、
| (3n)! ―――――――― n!n!n! |
◆東京都 GOFY・和人さんからの解答。
きょ〜ぉも お酒が 飲めるのわ〜っ・・・んっ、いいよ。この『数学の部屋』わ。
ここを眺めていると酔いが早く巡る。
酒のつまみに丁度いいなぁ。
なにしろ安く上がる。るんるん。
ところで何々??立方体の表面? んなの6個に決まっているぞぉ、昔から。
へぇ?南東リアルか? 解答を見るとぉ、mCn と北かぁ! ふむふむふむ。
なるひょど・・・あっれ〜? 南下 違和感がある象。
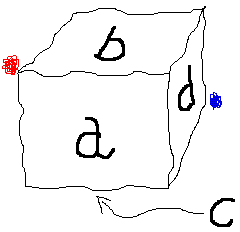
1×1×1の立方体で考えてみよか。
頂点●から出発して頂点●に、最短で到達する為には面を2つ通過するにゃぁ。
●から出発するときに選べるのは a,b,dの反対側 の3面。
最初に面aに来たと考えよう。
あと1面で●に到達するには、ふ〜っ
dまたはcの面に行くしかない象。
bにいっちゃ〜い缶!
つまりぃ、最短を洗濯する限りぃ、1つの面から次の面を選べるのは2コだけ。
じぇんぶで 参、弐が6通りアルジェ。
2×2×2の立方体・・・う〜ん説明が面倒だ。パスパス。
ただ最短通過面は5コ。
1つの面から次の面を選べるのは(最短である限り)常に2コだけ。
3×3×3 辺(稜線)に接しない面が出て北。
何か違いが出るかな??? ないない無い。
最短で8面通貨。次に選べるのは常に2面。
n×n×nの場合 最短通過面 3n−1。
3n−1 のそれぞれで次に選べるのは2面
だから 23n-1 通り。
●から最初に選べるのは3面
n×n×nの立方体の最短通過方法は 3×23n-1通り。
おお〜っと、最後の1面はもう選択肢が無いんだぁ。ふぇ〜、あぶいあぶい。
答:n×n×nの立方体の最短通過方法は 3×23n-2通りだいっ。
何だか簡単過ぎるなぁ。題意の取り違いかなぁ。
また「醤油問題か、ソースか、もう迷わねーズ」となるのかなぁ。
へくっ、大分酔いが回って北象。ええぃ!面倒くさい。
投稿しちゃえ。 おやすび〜。
◆神奈川県の大学生 ちょっこさんからの解答。
私も青木さんと同じでごじゃる。
この場合(描いてある図に従うと)、
奥に(長さ)n
右に同じくn
下に同じくn
だけ進まねばなりませぬ。
ということは、この問題は
{奥、奥、・・・、奥、右、右、・・・、右、下、下、・・・、下}
(奥・右・下ともn個ずつ並んでる)
という列があったとした時に、(異なる)並べ方はいくつ?という問題と同じと考えられまする。
青・赤・黄のボールがそれぞれn個ずつあります。何通りの並べ方があるでしょう?
という問題とも同じでございましょう。
で、そう考えると 求める答えは:
| (3n)! ―――――――― n!n!n! |
となりますなあ。
感想:合ってるのか間違ってるのかをはっきり知りたいです。
【コメント】
おお、ようやく私の味方が・・・・。とても嬉しいです。
無視されたらつらいな、と思っていたので。
少しだけ自信がもてました。
◆神奈川県 三島 久典 さんからの解答。
石川県 Takashi さんが正解だと思います。
つまり、清川さんの第1感、
3× 2nCnの修正版、
・正方形2つのつながりが3とおりではなく、6とおり
・かつ、重複するルートも6とおり
よって、6× 2nCn −6でOKだと思います。
青木さんの解、
| (a+b+c)! ―――――――― a!b!c! | は、 |
【コメント】
ようやく納得できました。
ついに解決したのではないでしょうか。
?マークをとります。