『Cosθπ』解答

◆愛知県　Y.M.Ojisan さんからの解答。

【解答】　ない。

【補題１】

　はaの整数係数多項式である。
ここでｎは自然数。

∵
　,　 　
と置くとき　α＋β＝a 　αβ＝１　である。

従って　

Ｆ(ｎ＋１、ａ)＝αn+1＋βn+1＝Ｆ(ｎ、ａ)(α＋β)−αβＦ(ｎ−１、ａ)＝ａＦ(ｎ、ａ)−Ｆ(ｎ−１、ａ)

Ｆ(ｎ、ａ)の最高次数はｎであってその係数は１である。

∵　Ｆ(ｎ、ａ)が多項式なら最高次数がｎであることは明らかである。　

２項展開式を用いれば　ａⁿの係数は　
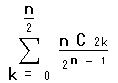であるが、一般に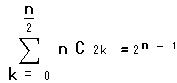であり、１である。

【補題３】

整数係数モニックｎ次多項式(最高次数の係数が１の多項式)＝０の解が有理数なら整数である。

∵　解を　ｘ＝

ｐ ｑ

(ｐ、ｑは互いに素)とするとき

式全体にｑⁿ　をかけるとモニックなので　
ｐⁿ＝ｑ×整数　と表される。

しかし　ｐとｑは互いに素なので　ｑは±１しか許されない。

【証明】

(Cosθπ＋iSinθπ)^2q=(Cosθ2qπ＋iSinθ2qπ)
の関係を用い、qを有理数θの分母とすれば右辺は１である。

一方、Cosθπ＝

a ２

−２≦a≦２　と置けば、補題１と２より

整数係数モニック多項式の方程式　Ｆ(２ｑ，ａ)＝２　が得られる。　

モニック多項式なので、補題３より　方程式の解で有理数のものは整数である。
よってaの可能性は０と±１と±２である。

即ち、Cosθπ＝０　or ±０．５　or 　±１　である。

よってθ＝０、

１ ３

、

１ ２

、

２ ３

、１のみである。

　『Cosθπ』へ

　数学の部屋へもどる