
◆滋賀県 ippei さんからの解答。
【問題1】
| 与えられた三角形と相似な斜辺の長さ | 6 |
の三角形 |
25÷12=2余り1であるから鳩の巣原理により、T2のどれか1つは内部または周上に3点を含む。
さらに、相似な三角形で斜辺の長さ2.9のものT3を考えると,
6 |
<2.9なのでT3はT2を完全に含むようにできる. |
このT3の斜辺を直径とする半円をT3を含む側に描くとこの半円が3点を含むものである.
【問題2】
左辺
=a*(b*c)
=c*(b*a)
=0*c*(b*a)
=0*(a*b)*c
=(a*b)*c
=右辺
◆山梨県 Footmark さんからの解答。
【問題7】
異なる4個のy値と異なる82個のx値の、任意の4x82個の格子点で考える。
(x値とy値を入れ替えても理屈は同じ)
x値が等しい格子点は82組あるが、どの組も格子点が4つある。
4つの格子点を3色以下で塗ると、2つ以上が同色である格子点がどの組にも存在する。
一方、4つ格子点の色の並びは81(=34)通りしかない。
それ故、82組では少なくともどこかの2組では色の並びが等しくなる。
(鳩の巣箱の原理)
その等しい2組においては、各組に2つ以上ある色の格子点は2組とも同色でy値も等しい筈。
よって、4頂点(格子点)が同色である長方形は必ず存在する。
【 補足 】
実際には、4x19個の格子点があれば4頂点(格子点)が同色である長方形は必ず存在します。
[ 証明 ]
4点の内の2点の選び方は以下の6(=4C2)通り。
××○○ , ×○×○ , ×○○× , ○××○ , ○×○× , ○○××
(×の色は無視して、少なくとも○は同色。)
よって、どの組の4点も上の6通りの内のいずれかの○の位置において同色である。
ところが3色あるので、○の色も区別すると18(=6x3)通り。
つまり、どのような4点も、この18通りのいずれかにならざるを得ない。
すると、19組あれば少なくともどこかの2組では○の色も位置も等しい筈。

よって、4x19個の格子点があれば、4頂点(格子点)が同色である長方形は必ず存在する。
証明終わり。
【P・S】
特に条件がなかったので、証明が分かり易い4x82の格子点で敢えて示しました。
「4X19個の格子点があれば存在することを示せ。」とすると、条件は厳しくなりますがヒントにもなってしまいます。
ここは、出題者も悩んだところではないかと思います。
◆ 出題者のコメント
ippeiさんは、下図のように分割されたんですね。美しいです!
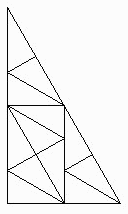
ちなみに私が考えたのは、下図のような分割でした。美しくない...
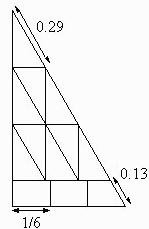
Footmarkさん、私は「4列あれば十分だな」ぐらいしか考えていませんでした。
(なんていいかげんな)
◆滋賀県 ippei さんからの解答。
【問題4】
方程式 x3+3ax2+2bx+c=0は0<x<1 に少なくとも1つの解を持つことを示す。
f(x)=x3+3ax2+2bx+c とおく。
f(x)をx=0からx=1 まで 定積分すると、
| 1 4 |
+a+b+c=0 となる。 |
y=f(x) は恒等的に 0 になる関数ではないので、0から1までの間に、正負両方の値をとる。
また、連続関数なので中間値の定理よりこの区間においてx軸と交わる。
このxの値が 0<x<1 を満たす解である。
【問題8半分】
f(x)=sin(sin(x))-sinxcosxとおく。
f(0)=0 、
f'(x)=cosx(cos(sinx)-cosx)+(sinx)2
ところで、この範囲で sinx<x なので cos の単調減少から
cos(sinx)>cosx.よって、f'(x)>0
従って、f(x)は単調増加だから、f(x)>0
すなわち
sin(sin(x))>sinxcosx が得られた。
◆山梨県 Footmark さんからの解答。
【問題3】
与式より、
| 1 x |
= | 1 z |
− | 1 y |
= | y−z yz |
。 |
そこで、y,z の最大公約数をmとし、
y=my' , z=mz' とすると、
| 1 x | = | y−z yz |
= | m(y'−z') m2y'z' |
= | y'−z' my'z' |
。 |
| 故に、 | m x | = | y'−z' y'z' |
。 |
ここで、条件よりx,y,zの最大公約数は1なので、mとxとは互いに素。
また、当然y'とz'も互いに素であるから、
(y'−z')とy'も、(y'−z')とz'も互いに素。
| それ故 | m x | も | y'−z' y'z' |
も既約分数である。 |
すると、m=y'ーz' , X=y'z'。
よって、x+y=y'z'+my'=y'(z'+m)=(y')2
明らかに x+y は平方数である。
証明終わり。
{ 補足 ]
条件を満たす例は、下式で与えられるため無限に存在する。
(ただし、p,qは互いに素な自然数。)
| 1 p(p+q) |
+ | 1 q(p+q) |
= | 1 pq |
◆愛知県 Y.M.Ojisan さんからの解答
【問題3】
問題の式を xy倍すると
| x+y | = | xy z |
であり、これをP=x+yとする。 |
a,bの最大公約数を<a , b> で表記する。
α=<x , z> β=<y , z> γ=<x , y> を用いて
x=αγX y=βγY z=αβZ とする。
このとき 条件<x , y , z>=1 より
<α,γ>=1 <β,γ>=1 <α,β>=1 である。
またαβγの定義より、
<γX,βZ>=1 <γY,αZ>=1 <αX,βY>=1 である。
これらを代入すると 下記である。
| P=x+y=γ(αX+βY) --(1) |
| P= | xy z | = | γ2XY Z |
--(2) |
<γX,βZ>=1 <γY,αZ>=1 より <γX,Z>=1 <γY,Z>=1である。
即ち(2)式が整数であるためには Z=1でなければならい。
従って(1)(2)より (αX+βY)=γXY --(3)
この式より βYはXの倍数である。
ところが <αX,βY>=1 であるから
<X,βY>=1であり、X=1である。
同様にY=1。
以上より P=γ2である。
すなわちx+yは平方数である。
【問題4】
| f(x)= | x4 4 |
+ax3+bx2+cx を考えると |
| 問題の方程式は | df(x) dx |
=0である。 |
| f(1)= | 1 4 |
+(a+b+c)=0 |
また、f(x)は恒等的に0ではなく、C1連続である。
従って、f(x)は開区間(0,1)で極値をもつ。
| すなわち ∃x∈(0,1)、 | df(x) dx |
=0である。 |
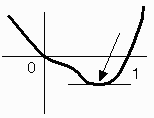
【問題5】
xを2以上の自然数とする。
x3−1=(x−1)(x2+x+1)であるから
x3≡1 mod (x2+x+1)である。
従って
x2(3p+k)+x3p+k+1≡x2k+xk+1 mod (x2+x+1)
p:整数 k=0,1,2である。よって
k=0 のとき
x2(3p+k)+x3p+k+1≡3 mod (x2+x+1)
{注:x=1だと ≡0 mod(1+1+1) なので x=1は除外されている}
k=1 のとき
x2(3p+k)+x3p+k+1≡x2+x+1≡0 mod (x2+x+1)
k=2 のとき
x2(3p+k)+x3p+k+1≡x+x2+1≡0 mod (x2+x+1)
つまり、 x2n+xn+1 は
nが3の倍数でないとき x2+x+1 の倍数である。
逆にx2n+xn+1が素数であるためには、nは0と1を除けば3の倍数でなければならない。
n=3pとすると
x2n+xn+1=(x*x*x)2p+(x*x*x)p+1 であり、
x*x*xをxと思えば同様にpも3の倍数でなければならない。
以上より nは0と1を除けば3のべき乗でなければならない。
初期x=2の場合
x2n+xn+1=4n+2n+1 であるから問題の与式であり、証明された。
【P.S.】
x=3,5のとき x2+x+1=13,31は素数なので、同じことがいえますね。
【問題6】
答え 0
∵ g(n)=(2n+1)f(n)2 とおくと
| g(n)= | (2n+1)(2n−1) (2n)2 |
g(n−1)である。 |
| 4n2−1 4n2 |
<1であるから |
| g(n)<g(n−1)<・・・<g(1)= | 3 4 |
である。 |
一方、
![]()
| よって | lim n→∞ |
f(n)=0 |
【P.S.】
| f(n)= | (2n)! n!n!22n |
=2nCn | ( | 1 2 | ) | 2n |
であるから、コインのトスの勝ち数と負け数が全く同じになる確率であり、0になることが想像できる。
◆滋賀県 ippei さんからの解答。
【問題6】
y=logx について平均値の定理を[1−t,1] で用いる。
| ただし、tは、0≦t≦ | 1 2 |
とする。 |
| 1<− | 1 t |
log(1-t)< | 1 1-t |
から、次の不等式を得る。 |
−2t<log(1-t)<−t・・・(1)
ところで、
| 1 2 |
=1− | 1 2 |
| 3 4 |
=1− | 1 4 |
| 2n−1 2n |
=1− | 1 2n |
を、(1)に代入すれば、
| log(1− | 1 2 |
)<− | 1 2 |
| log(1− | 1 4 |
)<− | 1 4 |
| log(1− | 1 2n |
)<− | 1 2n |
上の式を辺々加えると、
| log(1− | 1 2 |
)・(1− | 1 4 | )・・・(1− | 1 2n | )<− | 1 2 | (1+ | 1 2 |
+ | 1 3 |
+・・+ | 1 n | ) |
ここでn→∞ とすると 右辺は −∞
したがって 左辺も −∞
よってその真数は 0 に収束する。
p.s 難しかったです。