◆新潟県 加藤 英晴 さんからの解答。
【問題1】の凸多角形をより一般に円として答えます。
x−y平面で中心が原点の単位円で考えます。
その円を3本の無限直線で,交わりも隙間もない5領域に分割するためには,
3本の無限直線が少なくとも2つの交点をもち,そのうちの1つは円周上に,もう1つは円の内部に,残りの交点があればそれは円周上か円の外部にあり,かつ円周上の交点を通り円の内部にある交点は通らない無限直線は円の接線に
ならなければ十分です。
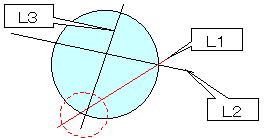
3本の無限直線をl1,l2,l3とします。
必ず周上にある1つの交点をl1とl2でできたものとし,
それを(1,0)と決めても一般性は失いません。
l1:y=ax−a(a<0),
l2:y=bx−b(b>0),
l3:y=cx+dとします。
交点は円の内部に1つしかないことを考慮すると,
l3は,円周の上部とl1とで囲まれる領域 と 円周の下部とl2とで囲まれる領域 との両方の内部を通ることが
できません。
もし通れたら,円が6領域に分割されてしまいます。
そこで今l3は,(円周の下部とl2とで囲まれる領域)の方を通らないとします。
すると必然的にその領域の面積はπ/5にならなければなりません。
そのようにするbが存在することは明らかです。
具体的には
| sin( | π 10 |
−b+ | b(b2+1) b2+1 |
)=b2− | 1 b2+1 |
後は,円から(円周の下部とl2とで囲まれる領域)を引いた
| 4π 5 |
の面積の領域を,c≧bの条件で, |
◆出題者のコメント。
発掘して頂いて大変ありがとうございます。
いくつかコメントがあります。
(1) をより一般に円として
正凸多角形の極限として円は存在しており、特殊な場合として円があります。
(2) これは凸図形の偶数等分の問題より可能です。
4分割可能と言っているだけです。
下図のようにL1と交わらないことを証明する必要があります。
