◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
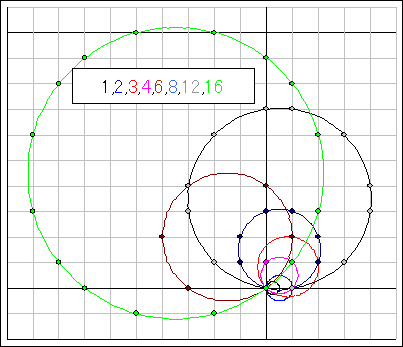
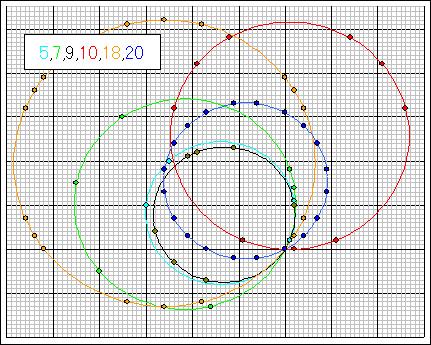
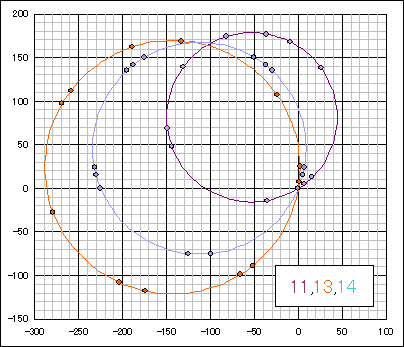
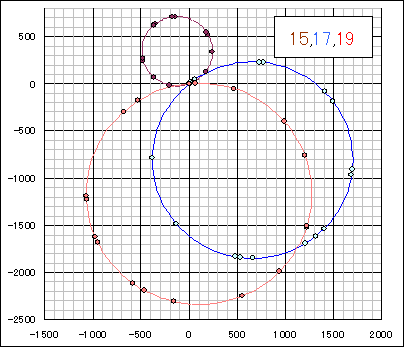
なるべく半径の小さいものであって、格子点数1〜20のものを下図に示す。
PC探索によった。
数値は添付ファイル参照。 計算結果

【問題2】
原点を中心とし、半径 4425=52132の円。
格子点は (0,4225) (4225,0) (0,-4225) (-4225,0) の4点と下記12点の8対称(上下鏡像、左右鏡像、90度回転)点の合計100点である。
(3000,2975), (3289,2652), (3380,2535), (3640,2145),
(3696,2047), (3713,2016),
(3900,1625), (4056,1183),
(4095,1040), (4180, 615), (4185, 580), (4199, 468)
【問題3】
任意の自然数nに対して、ちょうどn個の格子点を通るような円は、必ず存在すると言える。
(nが偶数の場合) n=2m+2 とすると
| ( | 1 2 |
, | 0)を中心とし、半径が | 2 |
である円 |
(nが奇数の場合) n=2m+1とすると
| (− | 1 4 |
, | 0)を中心とし、半径が | 5m 4 |
である円 |
【証明】
行列 Aを次のように定める。
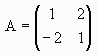
【Aの性質】
(1)tA×A=A×tA=5I である。
ここでIは単位行列。
∵ 計算すればよい。
| 従って、A-1= | tA 5 |
である。 |
![]()
即ち、A≡A5 mod 5でありこれを繰り返すだけなので、非対角成分が0になることはない。
(3)Akの対角成分は奇数で、非対角成分は偶数である。
∵2の剰余で考えるとAは単位行列である。
よって偶奇性は変化しない。
(4)A2kの対角成分は4を法として1であり、非対角成分は4の倍数である。
∵4の剰余で考えるとA2は単位行列である。
よって4の剰余性は変化しない。
(5)k1、k2∈Z Ak1=定数×Ak2 となるのはk1=k2のときのみである。
∵Aは正則で(1)により逆行列が存在する。
従って、(2)によりk1=k2のときのみである。
(6)成分が整数値のベクトルVがあってtVV≡0 mod 5 であるとき、
A-1VまたはtA-1Vは整数値ベクトルである。
∵Vx2+Vy2≡0 mod 5 であるためには、
Vx≡Vy≡0 mod 5 または
Vx≡±1 Vy≡±2 mod 5 または
Vx≡±2 Vy≡±1 mod 5 でなければならない。
Vx≡Vy≡0 mod 5であるとき
| (1)よりA-1= | tA 5 |
であるから、 |
| ベクトル GE(m、k、q)={Ak×tAm―k×(−1)q+I}×t( | 1 2 |
,0)を考える。 |
ここでk=0〜m q=0〜1である。
Aの性質(3)より
{Ak×tAm―k×(−1)q+I}の成分は偶数である。
よって、GE(m、k、q)は格子点である。
| 中心が( | 1 2 |
,0)、半径が | 2 |
である円を |
| (1)より|GE(m、k、q)− | t | ( | 1 2 |
,0)| | 2 | = | 5m 4 |
である。 |
| 即ち、GEは半径 | 2 |
のC1(m)上の点である。 |
| m=0ときC1(0)は半径が | 1 2 |
であり、 |
| これをW+ | t | ( | 1 2 |
,0)とすると、 |
| 即ち、2A−1W+ | t | ( | 1 2 |
,0)または2tA−1W+ | t | ( | 1 2 |
,0)は |
【奇数の場合】
| ベクトルGO(m、k)={Ak×tA2m―k−I}×t( | 1 4 |
,0)を考える。 |
Aの性質(4)より{Ak×tA2m―k−I}の成分は4の倍数である。
よって、GO(m、k)は格子点である。
| 中心が(− | 1 4 |
,0)、半径が | 5m 4 | である円をC2(m)と呼ぶことにする。 |
| (1)より|GO(m、k)+t( | 1 4 |
,0)|= | 5m 4 | である。 |
| 即ち、GEは半径 | 5m 4 | のC2(m)上の点である。 |
即ち、GO(m、k)により少なくとも2m+1個の格子点がC2(m)に存在することが分かる。
| m=0ときC1(0)は半径が | 1 4 |
であり、 |
| これをW+ | t | (− | 1 4 |
,0)とすると、 |
| 即ち、4A−2W+ | t | (− | 1 4 |
,0)または4tA−2W+ | t | (− | 1 4 |
,0)は |
【問題3解答蛇足1】
次の方法で 任意の自然数nに対して、ちょうどn個の格子点を通るような円は、必ず存在すると言える。
| (− | 1 4 |
, | 1+(−1)n 4 | )を中心とし、半径が | 4 |
である円 |
【問題3解答蛇足2】
n=4Mのとき 次の方法で、ちょうどn個の格子点を通るような円が存在すると予想される。
MがL個の2以上自然数の積に分解できるとします。
例えばn=100の場合 M=25=5×5ですから
25とすれば L=1、5×5なら L=2です。
すなわち ここでmjは2以上の自然数
そしてベクトルG4を次のように定めます。
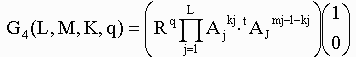
ここで kj=0〜mj−1、q=0〜3 また
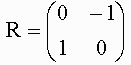
K=(k1,k2,k3,〜,kL)
M=(m1,m2,m3,〜,mL)
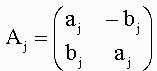
pj=aj2+bj2∈{奇素数}
i≠j ならば pi≠pj
このG4は整数値ベクトルでありK,qの組み合わせは全部で
4×m1×m2〜×mLです。
また |G4|2=Πpjmj−1 です。
つまり原点を中心とする半径√(Πpjmj−1)の円ではn個の格子点を持つと予想されます。
【証明】
大部分は前述の証明と同様に行えますが省略します。
問題は「 pj=aj2+bj2∈{奇素数}が無限に存在すること」や、
「Ajk=定数×Iになるk∈自然数がないこと」が一般に証明できていないことです。
従って予想です。
たとえば、無限の存在性の方は、4n+1型の素数が無限に存在することを算術級数定理などで証明する等の記述が必要です。
なお、n=100の場合解答は
p1=5(a=1 b=-2) と p2=13(a=2 b=3) m1=5 m2=5 として得た結果です。
この方が m=25を用いるより半径が小さくて済みます。
【感想】
意外に綺麗な関係があるのですね。
最初見たとき、もう少し複雑だろうと思っていました。
◆出題者のコメント。
Y.M.Ojisan さん、お疲れ様です。
出題の仕方がまずいせいで、解けないんじゃあないかと、心配していたところでしたが、解答してくださる方がいてありがたいです。
解答の中味についてですが、実は私の用意していた解答例は、複素数平面上のものだったので、少し読み替えに時間がかかっています。(行列が苦手なので)
しかし、大まかか流れは同じなので間違いないはずです。
一般に拡張しようとした場合、どうしても引っかかるのが、
「Ajk=定数×Iになるk∈自然数がないこと」の部分ですね〜。
ぐるっと回って同じものを何回も数えている、という事態になりかねません。
自分は複素数で考えていたので、互いに素である整数a,bについて、
「(a+bi)kが実数にならない」すなわち「arg(a+bi)=qπ(q∈有理数)とはならない」を示した
いのです。
直感的には成り立つだろうと思うのですが、やはり証明できません。
できないのだろうか?
追加するとしたら、逆行列を掛けたものが、格子点になることの証明の部分。
5の剰余類に分けて、どの場合も成り立つとしていますが、一般に拡張する場合、13の剰余類、17の剰余類、・・・と場合わけが増えて大変です。
剰余類を用いない証明はないでしょうか。
◆愛知県 Y.M.Ojisan さんからのコメント。
P=1+X2 である 4n+1型の素数PとXの組が無限に存在する点については次のページの[2]に証明が掲載されていました。
http://www80.sakura.ne.jp/~aozora/suuron/node31.html
つぎに複素数 Z=(X+i) を考えます。
フェルマーの小定理、P=4n+1、
PCK≡0 mod P when K=1〜P−1 などを用いると
ZP≡xP+iP≡X+i=Z mod P です。
つまり、フェルマーの小定理の複素数版風になります。
いま、 Zk=M:実整数 P>k>0 が在ったとします。
すると|Zk|2=M2 です。
一方、 |Z|2=1+X2≡0 mod Pです。
よって M2≡0 mod Pです。
つまり Pは素数ですから Zk=M≡0 mod P です。
これにZP−kをかけると ZP≡Z≡0 mod P です。
ところがZはmod Pで考えても0ではありません。
よって矛盾であり、 Zk=M:実整数 P>k>0は存在しません。
先の蛇足2解答には不正確な点が一つありました。
それは P=a2+b2 を満たすa≧b の組み合わせが1組である場合に限るという点です。
この場合には、逆行列の問題に関しても一般に剰余類の論法が普遍的に適用可能です。
よってそのようなPが無限に存在するのかが最後の問題でしょう。
あるいは、P=a2+b2 を満足するa≧b は使うなら全て使用する、としても成立しそうです。
この場合Pの無限性はOKですが、因数分解数Lに合わせられるかどうかが問題です。
ところが、実際に4n+1型の素数Pをパソコンで調べてみると、
少なくとも109までは全てのPをP=a2+b2であらわすことが可能で、かつ組み合わせが1個に限られています。
これが証明できれば完成なのですが。
◆出題者のコメント。
実は、Y.M.Ojisan さんの紹介にあったページの続きに、完璧な証明(と思しきもの)があります。
http://www80.sakura.ne.jp/~aozora/suuron/node45.html
上のページが読解困難な人のために(主に自分ですが(-_-;))証明の一部を具体的に考えてみました。
『a2+b2=pを満たす(a,b)の一意性(?)について』
実数でも純虚数でもない、異なる2つのガウス素数
α=a+bi と β=c+di があり、
ともに絶対値が√p(素数)であるとする。すなわち、
|α|2=a2+b2=p
|β|2=c2+d2=p
ここで、次の積を考える。(~は共役と考えてください)
αβ=(ac-bd)+(ad+bc)i
αβ~=(ac+bd)+(-ad+bc)i
絶対値が√pであるものどうしの積だから、これらの絶対値はpである。・・・(※)
ここで、一方の実部と、もう一方の虚部の積を考えると、
Re(αβ)・Im(αβ~)
=(ac-bd)(-ad+bc)
=-a2cd+abc2+abd2-b2cd
=-(a2+b2)cd+ab(c2+d2)
=p(ab-cd)
これは、0であるか、またはpの倍数である。
すなわち、Re(αβ)とIm(αβ~)の少なくとも一方は0か、pの倍数である。
すると、(※)より、αβとαβ~の少なくとも一方は、
±p+0i、または、0±pi である。
積が実数、または純虚数になるということから、βはαの同伴数か、その共役である。
したがって、a,bの順序と正負の区別をなくせば、(a,b)は一意に定まる。(終)
これは、『存在するなら一意である』ことの証明であり、 『常に一意に存在する』ことの証明ではないので、ほんとに証明の一部です。
なお、ガウス素数等の用語の解説は上で紹介したページが詳しいです。
◆愛知県 Y.M.Ojisan さんからのコメント。
(1)前回のコメントの冒頭部分ですが、誤解をしていました。
参照ページの[2]は4N+1型素数の無限存在性を証明しているだけでした。
(2) 複素数版風のところですが、これは Z=X+Yiでも成立し、以降の議論は問題ありません。
(3) 問題のP=a2+b2の存在・唯一性は フェルマー・オイラーの定理ないし2平方和の定理として基礎定理のようです。
(素人数学の弱みです)“
下記ページ参照。
存在性の方はフェルマーも不完全でオイラーが完成したとあるので難しいのでしょう。
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Prime_numbers.html