『円に内接する多角形の面積』解答

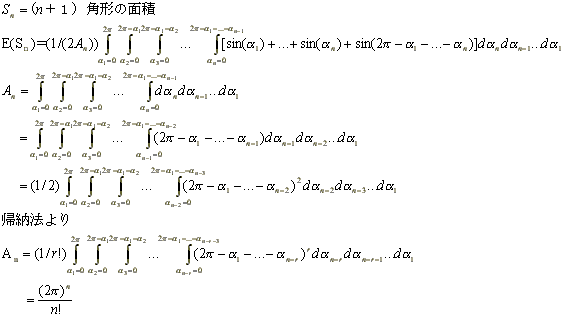
◆宮城県　アンパンマン さんからの解答。

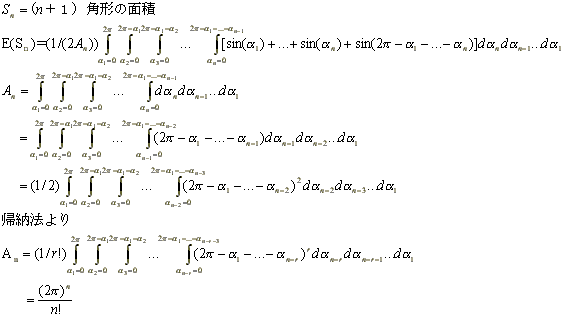
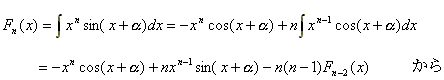
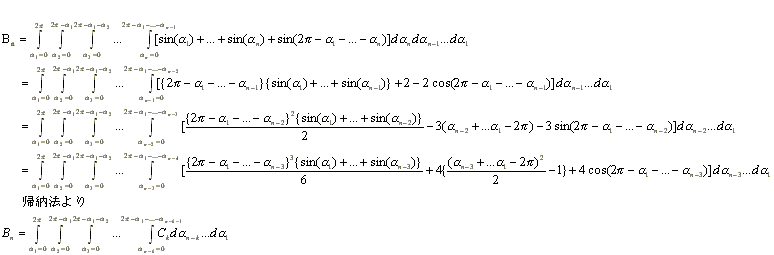
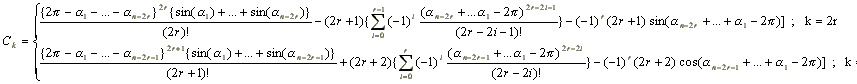
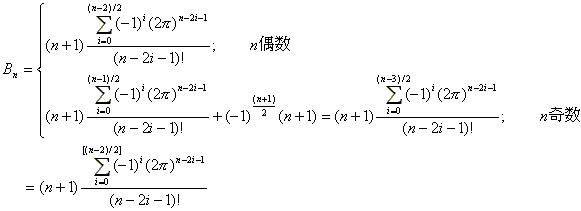
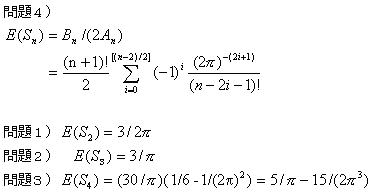
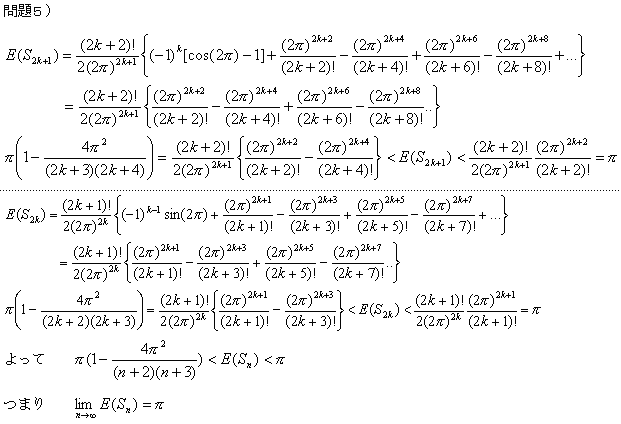
◆愛知県　juin さんからの解答。

【問題１】

円周上に、反時計周りに点A,B,Cをとる。
円の中心をOとし、
x₁=∠BOC,x₂=∠COA,x₃=∠AOCとする。

x₁≧0,x₂≧0,x₃≧0,x₁+x₂+x₃=2π

△ABCの面積Sは、

S=

1 2

sinx1+

1 2

sinx2+

1 2

sinx3=

1 2

(sinx1+sinx2+sinx3)となる。

ここで、確率を次のように入れる。

Ω＝[0,2π)×[0,2π)×[0,2π)

この空間の中で、x₁+x₂+x₃=2πとなる平面（正三角形）の上で、面積に比例した確率を入れる。

△ABCの面積Sの平均ESは、次のようになる。

S=E(

1 2

(sinx1+sinx2+sinx3))=

1 2

(Esinx1+Esinx2+Esinx3)

ここで、Esinx₁=Esinx₂=Esinx₃だから、Esinx₁だけ計算する。

まず、確率分布は

P(x1＞t)=

(

2π-t 2π

)

2

=(1-

t 2π

)

2

だから、

P(x1≦t)=1-

(1-

t 2π

)

2

tで微分して、密度関数f(t)=

2(2π-t) (2π)2

この密度関数を使い、sinx₁ を[0,2π)で積分する。

Esinx₁

=∫

sint×2(2π-t) (2π)2

dt

=

2 (2π)2

∫sint×(2π-t)dt

=

2 (2π)2

∫sint×(-t)dt

=

2 (2π)2

×2π

=

1 π

ES=

1 2

･3Esinx1=

1 2

･3･

1 π

=

3 2π

【問題２】

単位円周上に反時計周りに４点A,B,C,Dをとる。
単位円の中心をOとする。
x₁=∠AOB,x₂=∠BOC,
x₃=∠COD,x₄=∠DOAとする。

内接四角形ABCDの面積

S=

1 2

(sinx1+sinx2+sinx3+sinx4)となる。

ここで、確率を次のように入れる。

Ω＝[0,2π)×[0,2π)×[0,2π)×[0,2π)

Ωの中の空間（正四面体）x₁+x₂+x₃+x₄=2πの体積に比例した確率を入れる。

面積Sの期待値

ES=E(

1 2

(Esinx1+ Esinx2+ Esinx3+ Esinx4)

=

1 2

(Esinx1+ Esinx2+ Esinx3+ Esinx4)

ここで、Esinx₁= Esinx₂= Esinx₃= Esinx₄　　なので、
Esinx₁だけ計算する。

P(x1＞t)=

(

2π-t 2π

)

3

=(1-

t 2π

)

3

P(x1≦t)

=1-(1-

t 2π

)

3

tで微分して、密度関数はf(t)=

3 (2π)3

(2π-t)

2

となる。

Esinx₁は,sinx₁をこの密度関数で、[0,2π)の範囲で積分すれば良い。

Esinx₁

=∫sint×

3 (2π)3

(2π-t)2dt

2π-t=sとして、

=

3 (2π)3

∫(-sin(s)s2)ds

=

3 (2π)3

(2π)2

=

3 2π

ES=4×

1 2

×

3 2π

=

3 π

答　内接四角形の面積の期待値は、

3 π

【問題３】

単位円周上に反時計周りに、５点A,B,C,D,Eをとる。
単位円の中心をOとし、
x₁=∠AOB,....,x₅=∠EOAとする。

x₁+x₂+x₃+x₄+x₅=2π　となる。

五角形ABCDEの面積Sは、

S=

1 2

(sinx1+sinx2+sinx3+sinx4+sinx5) となる。

ここで、確率を次のようにいれる。

Ω＝[0,2π)×[0,2π)×[0,2π)×[0,2π)×[0,2π) とし、
この中の、x₁+x₂+x₃+x₄+x₅=2π　となる、部分集合（４次元の正三角形に相当する図形）に、４次元の体積に比例して、確率を入れる。

ES=E(

1 2

(sinx1+sinx2+sinx3+sinx4+sinx5))=

1 2

(Esinx1+......+Esinx5)

ここで、Esinx₁=.....=Esinx₅ だから、Esinx₁　だけ計算する。

P(x1＞t)=

(

2π-t 2π

)

4

だから、

P(x1≦t)=1-

(

2π-t 2π

)

4

tで微分して、密度関数は、

4 (2π)4

(2π-t)3

となる。

Esinx₁は、sinx₁をこの密度関数で、[0,2π)の範囲で積分した値である。

Esinx₁

=∫

sint×4 (2π)4

(2π-t)3 dt

ここで、2π-t=sとすると、

=

4 (2π)4

∫(-s3)sin(s)ds

=

4 (2π)4

((2π)3-12π)

ES=

1 2

×5×

4 (2π)4

((2π)3-12π)=

5 π

-

15 2π3

【問題５】

単位円周上に反時計周りに点をとり,A₁,A₂,...,A_nとする。
単位円の中心をOとし、∠A₁OA₂=x₁,...,∠A_nOA₁=x_nとする。
x₁+x₂+...+x_n=2πとなる。

n角形の面積S(n)=

1 2

(sinx1+...+sinxn)となる。

ここで、確率を次のようにいれる。
Ω=[0,2π)ⁿとする。

Ωの中の(n-1)次元部分集合、x₁+x₂+...+x_n=2πの上で、(n-1)次元の体積に比例した確率を入れる。
この確率で平均を計算する。

ES(n)=

1 2

(Esinx1+...+Esinxn)となる。

Esinx₁=...=Esinx_nだから、Esinx₁ だけ計算する。

分布関数は、

P(x1＞t)=

(

2π-t 2π

)

n-1

より、

P(x1≦t)=1-

(

2π-t 2π

)

n-1

となる。

tで微分して、密度関数は、

f(t)=

(n-1)(2π-t)n-2 (2π)n-1

=(n-1)(1-

t 2π

)

n-2

/(2π)となる。

Esinx₁は、sinx₁をこの密度関数で、[0,2π)の範囲で積分すれば良い。

Esinx₁=∫sin(t)f(t)dt

S(n)=

1 2

n∫sin(t)f(t)dt=

1 2

n∫{sin(t)(n-1)

(1-

t 2π

)

n-2

/(2π)}dtとなる。

（計算力が無いので、問題４の解答は完成できません。）

S(n)を部分積分する。
sin(t)を微分し、密度関数を積分する。

S(n)

=

1 2

{n[sin(t)

(1-

t 2π

)

n-1

(-1)]-n∫cos(t)

(1-

t 2π

)

n-1

(-1)dt

=

1 2

{n(0-0)+∫cos(t)n

(1-

t 2π

)

n-1

}dt

=

1 2

{[cos(t)

(1-

t 2π

)

n

(-2π)]-∫(-sin(t)

(1-

t 2π

)

n

(-2π)dt}

=

1 2

{0-(-2π)-∫sin(t)

(1-

t 2π

)

n

(2π)}dt

=π-π∫{sin(t)

(1-

t 2π

)

n

}dt

積分を評価すると、|sin(t)|≦1だから、

|∫{sin(t)

(1-

t 2π

)

n

dt|≦

∫(1-

t 2π

)

n

dt=

2π n+1

よって、|S(n)-π|≦

π(2π) n+1

→0 (n→∞)

つまり、limS(n)=π　(n→∞)

　『円に内接する多角形の面積』へ

　数学の部屋へもどる