◆宮城県 甘泉法師 さんからの解答。
【問題1】
円C : x2 + y2 = c2
点A :(a,0)
題意の円の中心:(b cos θ, b sinθ)とする。
c2 + b2 = (b cos θ - a)2 + (b sinθ )2 から
| 直線x =b cos θ= | a2 - c2 2a |
つまり、軌跡は円Cと点Aを結ぶ直線に垂直。
第一項の長さは長さaの線分の二等分で、第二項の長さは長さcの線分のc/2a倍でともに容易に作図で求められる。
【問題2】
円A : x2 + y2 = a2
円B : (x-p)2 + y2 = b2
題意の円の中心:(c cos θ, c sinθ)とする。
c2 + a2 = (c cos θ - p)2 + (c sinθ )2 + b2 から
| 軌跡は直線 x = c cosθ = | p2 + b2 - a2 2p |
【問題3】
(2)問題2の設定を使う。
円A : x2 + y2 = a2
円B : (x-p)2 + y2 = b2
題意の円の中心:(c cos θ, c sinθ)
| 軌跡は直線 x = α = | p2 + b2 - a2 2p |
題意の円の方程式は
(x - α)2 + (y - β)2 = α2 + β2 + a2 .
| これから β = | x(x-2α) + y2 - a2 2y | と解くと |
任意の点を通る円が存在する。
βの長さは容易に作図で求められる。
(1)(2)でb=0とする。
(3)(2)の設定を使う
円の方程式 (x - α)2 + (y - β)2 = α2 + β2 + a2
が第3の円 中心 (c cosθ, c sinθ)、半径r の直径の両端を通るとすると
| β = | x(x-2α) + y2 - a2 2y | から |
| β = | (c cosθ + r cosφ)(c cosθ + r cosφ-2α) + (c sinθ + r sinφ)2 - a2 2(c sinθ + r sinφ) |
| = | (c cosθ - r cosφ)(c cosθ - r cosφ-2α) + (c sinθ - r sinφ)2 - a2 2(c sinθ - r sinφ) |
これを解くと
| cotξ = | (c2 + r2 - a2) cotθ - 2αc cosecθ c2 + a2 - r2 |
これから作図で容易にφが求められ、βも得られる。
◆愛知県 Y.M.Ojisan さんからの解答。
【補題】
2円の直径を通る円の作図方法
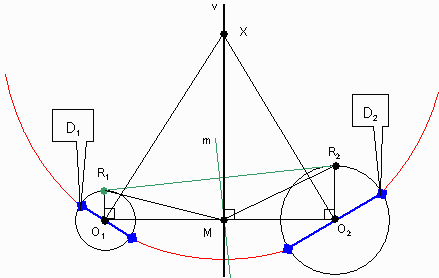
下図参照。
(1)2円の中心をO1、O2とし、半径を線分O1O2に直交する方向にR1、R2とします。
O1R1=r1,O2R2=r2
(2)線分R1R2の垂直2等分線mと線分O1O2の交点をMとします。
従って、R1M=R2M=p
(3)Mをとおり、線分O1O2に垂直な直線v上に点Xをとります。
XM=h
(4)XO1に直交する方向に円O1の直径を、XO2に直交する方向に円O2の直径をとります。
このときXを中心とし両円の直径端[D1 D2でそれぞれ代表]を通る円を描くことがでます。
∵
XDk2
=XOk2+rk2
=XM2 +MOk2+rk2
=p2-rk2+h2+rk2
=p2+h2 for k=1,2

【問題1】
軌跡は直線。
作図は補題の方法においてr2=0とすればよい。
【問題2】
補題による。
【問題3】
3個の円から選んだ(2個の円の組)の2組を用いて直線vを2本作図し交点を求める。
円の中心は1直線上にないので、O1O2に垂直なvは必ず交差する。
その点が問題を満たすことは明らかである。
すなわち(3)が証明された。
(1)(2)は(3)の方法において半径が0である場合である。
◆出題者のコメント。
素早い回答ありがとうございます。正解です。
簡単すぎたでしょうか。
今読み返してみると、『作図する方法を〜』とかいてある時点で、直線か円しかないことがばればれでしたね。
直径の両端という、不確定な要素を含みながらも、軌跡が直線になるというところが面白くて記憶に残っていた問題で
した。