◆宮城県 甘泉法師 さんからの解答。
折り目が円の接線(名前1)になるように紙を折る。
同様に円の接線2、接線3の折り目をつける。
接線1と接線2が重なるように紙を折った折り目(名前1)の上に円の中心がある。
接線1と接線3が重なるように紙を折った折り目(名前2)の上にも円の中心がある。
折り目1と折り目2の交点が円の中心である。
感想:「鉛筆」、「A4サイズ:210mm * 297mm」、「半径12cm前後」に意味があるのでしょうか。
◆神奈川県 かるがも1号 さんからの解答。
円への接線となるよう、紙を内側に(円が見えるように)折る。
同様の作業を2回行い、2本の接線の交点が角となり、2本の接線が重なるように、用紙を2つに折る。
すると、これが、円の中心を通る線となる。
同様の作業を2回行うことにより、別の中心線を折り、2本の中心線の交点が、円の中心となる。
◆神奈川県の中学校2年生 をめが さんからの解答。
A4の紙にかかれているんだから長方形の紙だろうと妄想を膨らませて、
◆愛知県 Y.M.Ojisan さんからのコメント。
出題者の期待した解は「をめが」さんのものと推定されます。
ただ、折って良い場合、実用的には次のようにA4と実質鉛筆なしでもできます。

適当に中心近く円にかかるように黒線で山折します。
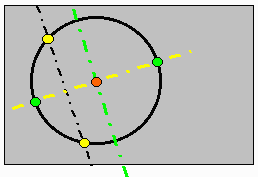
折ったまま円と黒線の交点(黄色)が重なるように黄色線で山折します。
黄色線は直径になります。
一度開いて、黄色線で山折します。
円と黄色線の交点(緑色)が重なるように緑線で山折します。
黄色線と緑色線の交点(赤点)に鉛筆で点を打ちます。
緑色線も直径です。
従って赤点は中心です。
なお、紙を折ってはいけないとすると、接線で折るよりさらに至難の業ですが、次のように鉛直に俯瞰し、円と鉛筆の上の円を重ねてから、鉛直に鉛筆を落とすぐらいしか思いつきませんでした。
無理ですけどね!
◆千葉県 なのはな子 さんからの解答。
*『問題』に意味もなく「A4サイズの紙に、直径12cm前後の円」とあるとは考えにくいです。
「直径12cm前後の円」の、『前後』という言葉がビミョウです。
例えば、直径が長方形の紙の横の長さと同じ円が、適当な位置に書いてあるとします。
(紙を縦長にして見る)
円の中心は、縦に二つ折りにした時の折線上に必ずあります。
次に、横に二つ折、四つ折、八つ折・・・と、どんどん折ります。
円の直径となる線は必ずどこかにあります。
円の直径になる縦と横の折線の交わるところが円の中心です。
推測ですが、「A4サイズの紙に、直径12cm前後の円」の中心も、同様にして求められるのではないか?・・・と考えてみました。
折る回数の数え方は、(2,4,8,16,32・・・)となるガマの油の口上みたいな数え方です。
「A4サイズの紙」を縦に5回折ると、6.6mmごとに折線がつきます。
210÷32=6.5625
6.6X18=118.8 ・・・120mmに微妙に近い。
「直径12cm前後の円」の外側に接する2本の線がわかります。
円の内側の折線を数えると直径になる線もわかります。
次に、横にも5回折ると、9.2mmごとに折線がつきます。
297÷32=9.28125
9.3x13=120.9 ・・・120mmに微妙に近い。
「直径12cm前後の円」の外側に接する2本の線がわかります。
円の内側の折線を数えると直径になる線もわかります。
この縦と横の折線の交わる点が「A4サイズの紙に、直径12cm前後の円」の中心です。
折線の数を数えるだけなので、定規もコンパスも不要、紙が裏側から透けて見える必要もありません。
◆出題者の山梨県 Footmark さんからのコメント。
みなさん、解答ありがとうございます。
いろいろな方法があるものですね。
Y.M.Ojisan さんがご察しのように、出題者として期待したのは、「をめが」さんの方法でした。
(そのため、紙を方形であるA4サイズにし、鉛筆も用意しました。)
これまでに示された方法を要約すると、次の3つですね。
(1)接線折り (2)円周角折り (3)重ね折り
そこで、これらのそれぞれの特徴を表にしてみると、次のようになりました。
| 接線折り | 円周角折り | 重ね折り | |
| 難易性 | 難 | 易 | 易 |
| 折れ線の最少数 | 5 | 4 | 3 |
| 記入点の最少数 | 0 | 4 | 0 |
こうしてみると、Y.M.Ojisan さんの「重ね折り」が現状では1番優れているようですね。
裏側から透けて見えなくても、折った状態のまま次を折れば、紙の内部の2点は辺上の2点となるので重ねることが可能です。
なるほど、うまい方法もあるものですね。とても勉強になりました。
それから、鉛筆を落とすのはとても面白いので「いただき」です。
これを、数学好きの友人たちに出題して、馬鹿うけしようとひそかに思っています。
6角柱の鉛筆だとまずいので、そのときは色鉛筆にするつもりです。(笑)
なお、円を直径12㎝前後としたのは、特にその大きさでなければならないというのではなく、
現実的に可能とするため、ある程度の大きさがある円であることを示したかっただけです。
折れ線の幅は紙質や紙厚により違いますが、いずれにしても無視できない幅を持ちます。
あまり小さい円だと、円に対し折れ線の交点の占める割合が多すぎて、「中心点を求めた」とは言いにくいからです。
◆愛知県 Y.M.Ojisan さんからのコメント。
紙を折らない方法で意外に精度が高い方法がありました。
ぴかぴかの机の上に紙を置き、鉛筆削りでよく尖らせた鉛筆で、中心と思しき点を押さえます。
目を可能な限りレコード針よろしく円の接線方向で近づけます。
そして紙をくるくる回します。
中心でなければ線がゆれるので、少しずつ修正してゆきます。
重ね折り程度の精度は出るようです。
ところで、紙の角を利用して直径を得る方法は面白い発想なので、何とか角の利用がMUSTな問題設定はないものかと考えてみました。
これでも手数をかければMUSTではないのですが。
【追加問題】
A4(297mm×210mm)の紙上にほぼ直径120mmの円が書かれています。
ただし、円の中心の位置は紙の中心とは限りません。
定規もコンパスもなく、あるのは1本の鉛筆だけで、紙に書くことが許されるのは点だけです。
紙上どこに円があっても円の中心を求めることができる統一的な方法はあるでしょうか?
なるべく手順数の少ないものを考えてください。
ただし、
(1)紙は裏側から透けて見えないものとします。
(2)紙を破ってはいけません。
(3)円内(表裏)には、点を打つ以外の加工を残してはいけません。
◆宮城県 甘泉法師 さんからの解答。
【追加問題】
紙の4辺に平行な折り目で円に外接する正方形をつくる。
頂点に外接し辺と45度をなす折り目をつける。
297 = 148.5 * 2 > 120 * 2 から、円の位置にかかわらず半径が148.5cmより小さければ「45度をなす折り目」どおしの交点が必ずひとつはある。
正方形の辺でおりかえし交点を円にあてて中心を得る。
◆愛知県 Y.M.Ojisan さんからのコメント。
なるほど。
正方形のうち1辺は不要なので 手数:5 と認定しましょう。
目標は3です。
◆出題者の山梨県 Footmark さんからのコメント。
なのはな子さん、解答ありがとうございます。
A4用紙の特性と12cm前後の円の特性を利用したうまい方法ですね。
とても面白い発想だと思います。
◆山梨県 Footmark さんからの解答。
【追加問題】
紙の角(かど)Rが円周角になるように紙を折って(谷折り)、円周と交差する辺上の2点P,Qを得る。
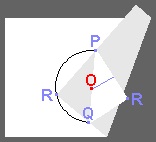
その状態から、直線PQで角(かど)Rだけを反対側に折り返す。(山折り)
1度開いてから、2点P,Rが重なるように折って、直線PRの垂直2等分線を折れ線(青線)で得る。
すると、その折れ線(青線)は、折れ線PQの中点Oを通る。
そこで、既にある折れ線に従って再度最初と同様に、角(かど)Rが円周角になるように折ってから、折れ線PQで角(かど)Rだけを折り返すと、点Oは円の中心にある。
よって、点Oと重なっている半円側の点に鉛筆でしるしを付ければ、それが紙に書かれた円の中心である。
【P・S】
折れ線3本,記入点1つになりました。
折れ線の精度を考え、あえて2枚以上を重ねて折ることを避けてみました。
(折れ線の精度は明らかに、1枚を折るときよりも2枚同時に折るときの方が劣ります。)
◆愛知県 Y.M.Ojisan さんからのコメント。
Footmarkさん本家には失礼ながら、私の期待した解答ありがとうございます。
ただし、解答としては円内に折り線がかからないことの証明を希望します。
◆山梨県 Footmark さんからの解答。
【追加問題】
円の位置によらない、統一的方法の詳細は以下です。
(1) 紙の長い方を縦にして、円から1番離れていると思われる紙の頂点Rを下側にします。
(2) その頂点Rを、円周の最上部あたりの点に合わせで紙を折ります。 ……(1本目)
(折る前の頂点Rから、円周の最上部の仰ぎ角は必ず45°よりも大きいため必ず円周角になります。)
(3) その状態から、直線PQで頂点Rだけを反対側に折り返します。 ……(2本目)
(4) 一度紙をすべて開いてから、2点P,Rが重なるように紙を折ります。 ……(3本目)
このとき、この3本目の折れ線は折れ線PQとPQの中点Oで交差します。
(5) 紙を開いてから、既にある折れ線に従って再度1本目,2本目を折ると、点Oは円の中心にあります。
(6) 点Oと重なっている半円側の点に鉛筆でしるしを付けると、そこが紙に書かれた円の中心です。
【3本の折れ線とも円内に入らない証明】
元々が作図問題でしたから、あえて作図で証明してみました。
(本当は細かい計算が面倒なだけだったりして…。)(^^;
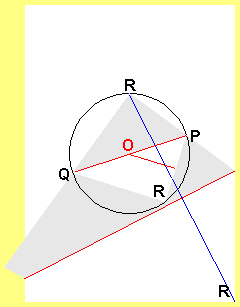
図はA4サイズ(縦297㎜×横210㎜)の紙の真ん中に直径120㎜の円を正確に書いたものです。
1番目の折れ線は図の青線の垂直二等分線です。
それ故、青線が短いときほど折れ線が円内に入る可能性が当然高くなります。
ところが、青線が最短であるときでさえ、図のように辛うじて折れ線は円外にあります。
よって、1番目の折れ線が円内に入ることはあり得ません。
2番目の折れ線PQは、図の下にある白い台形(三角形のときもある)内にあるので円内に入らないのは明らかです。
3番目の直線PRの垂直二等分線である折れ線ですが、
これは紙をすべて開いて考えると、下辺からPRの半分の距離にある下辺に平行な直線です。
PRは直径未満ですから120㎜未満であり、その半分なら当然60㎜未満です。
一方、円が紙の最下位置にあるときでさえ、下辺から円周までの距離は(297-120)㎜の半分の88.5㎜あります。
よって、3番目の折れ線も円内に入ることは明らかにあり得ません。
証明は終わりです。
◆愛知県 Y.M.Ojisan さんからのコメント。
Footmarkさん証明ありがとうございました。
12cmはA4の対角線長の3分の1より若干短い長さであり、そのような意味があるようです。
どこまで大きな円が可能かなども数学の問題にはできますが、実用的ではないようです。
◆東京都 建築家 さんからの解答。
まず紙の角を円周上に当てて角との交点をR、紙の辺との交点をP、Qとします。
次にまた広げて他の角を用いて今度はその角をP、Qのどちらかにあて、紙の辺がRも通るように重ねます。
すると紙の縁と円周の交点はP、QのどちらかとR、そしてもう一つ新しい点Sになります。
するとこの4点は長方形になりますので、後はSR、PQの交点を紙の辺を使って求めれば中心Oがもとまります。
(計4手)
はたして2つ目の角が上手くそのように重ねられるかが問題です。
(追加問題?)
ヒントは紙は折らないと言ったとこでしょうか。