俀
仧搶嫗搒丂偐偊傞 偝傫偐傜偺夝摎丅
亂栤戣侾亃
亙夝侾亜
俛偐傜俙俠偵悅慄傪壓傠偣偽乮偦偺懌傪俫偲偡傞乯丄俀偮偺嶰妏掕婯偵側傞丅
| 俠俫亖 | 侾 俀 | 俛俠 |
| 俙俫亖俛俫亖 | 俀 | 俛俠 |
| 侾 俀 | 俛俠 | 亄 | 俀 | 俛俠亖侾 |
亙夝俀亜
惓尫掕棟傪巊偆丅
倱倝値俈俆並偼倱倝値乮係俆並亄俁侽並乯偺壛朄掕棟傛傝媮傔傞丅
亂栤戣俀亃
椉曈們倧倱2兤偱妱傞丅
倲亖倲倎値兤偲偟偰丄
侾亄倲2亅係倲亖侾亅倲2佁丂倲亖侽丆俀
傛傝丄倲倎値兤亖侽丒丒丒亂摎亃
亂栤戣俁亃
攞妏偺岞幃傪俀夞巊偆丅
| 侾俇侽乮 | 侾亅們倧倱俀兤 俀 | 乯乮 | 倱倝値俀兤 俀 | 乯亅俉侽乮 | 倱倝値俀兤 俀 | 乯亄侾俉乮 | 倱倝値俀兤 俀 | 乯2 |
| 亖亅係侽倱倝値俀兤們倧倱俀兤亄 | 俋 俀 | 乮倱倝値俀兤乯 | 2 |
| 亖亅係侽乮 | 倱倝値係兤 俀 | 乯亄 | 俋 俀 | 乮 | 侾亅們倧倱係兤 俀 | 乯 |
| 亖 | 俋 係 | 亅俀侽倱倝値係兤亅 | 俋 係 | 們倧倱係兤 |
| 亖 | 俋 係 | 亅 | 併俇係俉侾 係 | 倱倝値乮係兤亄兛乯 |
| 嵟戝抣丗 | 俋 係 | 亄 | 併俇係俉侾 係 | 丒丒丒亂摎亃 |
| 嵟彫抣丗 | 俋 係 | 亅 | 併俇係俉侾 係 | 丒丒丒亂摎亃 |
亂栤戣係亃
侾偲俙偐傜併俙傪嶌恾偡傞曽朄偼埲壓偺捠傝偱偁傝丄偙傟傪曽朄仏偲屇傇丅
捈宎侾亄俙偺敿墌傪昤偔丅
捈宎忋偺抂揰偐傜侾偺揰偱悅慄傪棫偰偨偲偒偵丄
悅慄偲敿墌偲偺岎揰偲悅慄偺懌偺嫍棧偼併俙丅
曽朄仏傪梡偄偰丄侾們倣偲俁係們倣偐傜併俁係們倣傪昤偔丅
師偵乮俇亄併俁係乯們倣傪昤偔丅
曽朄仏傪梡偄偰丄侾們倣偲乮俇亄併俁係乯們倣偐傜併乮俇亄併俁係乯們倣傪昤偔丅
仧弌戣幰偺僐儊儞僩丅
栤戣侾偼惓夝偱偡丅
偟偐偟丄栤戣偵偼彂偄偰偄傑偣傫偑拞妛惗偺廗偭偨斖埻偱俀捠傝偺夝偒曽偑偁傝傑偡丅
傕偪傠傫丄壛朄掕棟傪梡偄偰偔傟偰傕椙偄偺偱偡偑丄偦偪傜偺夝摎傕扵偟偰傒偰偔偩偝偄丅
栤戣俀偼搑拞偱t=0,2偲弌偟偰偔傟偰偄傞偺偵tan兤=0偲側偭偰偄傞偺偼壗屘偱偟傚偆偐丅
tan兤偼慡偰偺幚悢傪摦偔偺偱tan兤=2傕惉傝棫偮偼偢偱偡丅
栤戣俁偼惓夝偱偡丅
偙偺栤戣偼杔偺愝掕儈僗偱摎偊偑曄側抣偵側偭偰偟傑偄傑偟偨丅
傎傫偲偼18sin2兤cos2兤偱偼側偔偰36sin2兤cos2兤偩偭偨傫偱偡傛丅
栤戣係偺偙偺嶌恾曽朄偩偲捈慄偺杮悢偱尵偆偲嵟弶偺敿墌傪彂偔帪偵堦杮丄悅慄傪棫偰傞帪偵堦杮丄俀屄栚偺墌偵悅慄傪棫偰傞帪偵堦杮偲側傝傑偡偹丅
杔偺峫偊偰偄偨傛傝偄偄曽朄偱偡偹丅
偟偐偟丄偙偺曽朄偩偲嶌恾偵梡偄傞巻偼墶35噋丄廲35/2噋偼昁梫偵側傝傑偡偹丅
杔偺峫偊偰偄偨曽朄偱偼捈慄偼係杮昁梫側偺偱偡偑梡偄傞巻偼廲墶5噋巐曽偱嶌恾偱偒傑偡丅
偤傂丄偦偪傜偺曽朄傕扵偟偰傒偰偔偩偝偄丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂栤戣係 偦偺侾亃
巻偺戝偒偝偺傎偆偵偙偩傢偭偰尒傑偟偨丅
侾丏俆們倣亊係們倣傎偳偁傟偽俷俲偱偡丅
捈慄偺悢偊曽偑堘偆偐傕抦傟傑偣傫偑丄堦墳俁杮偱偡丅
乮侾乯壓恾偺傛偆偵暘搙婍丄掕婯偱捈岎慄乮惵丄愒乯傪昤偒丄傕偺偝偟偱墶慄偺忋偵侽丏俆們倣丄侾們倣偺揰丄丂廲慄偺忋偵侾們倣丄俀們倣偺揰傪偲傝傑偡丅
乮俀乯壓恾偺傛偆偵侽丏俆們倣偲俀們倣偺揰傪寢傇捈慄傪掕婯偱堷偒傑偡丅
| 偙偺揰娫偺嫍棧偼 | 俀 | 們倣偱偡丅 |
乮俁乯僐儞僷僗傪梡偄偰廲墶侾們倣偺揰娫偺嫍棧乮![]() 乯傪偲傝丄乮俀乯偺捈慄忋偱俀們倣偺揰偺岦偙偆偵嫍棧
乯傪偲傝丄乮俀乯偺捈慄忋偱俀們倣偺揰偺岦偙偆偵嫍棧![]() 們倣偺揰傪偲傝傑偡丅
們倣偺揰傪偲傝傑偡丅
乮係乯僐儞僷僗傪梡偄偰侽丏俆們倣偺揰傪拞怱偲偟丄乮俁乯偱昤偄偨揰傪捠傞墌傪昤偒丄廲慄偲偺岎揰傪媮傔傑偡丅
乮俆乯乮係乯偱摼偨岎揰偲尨揰偺嫍棧偑媮傔傞抣偱偡丅
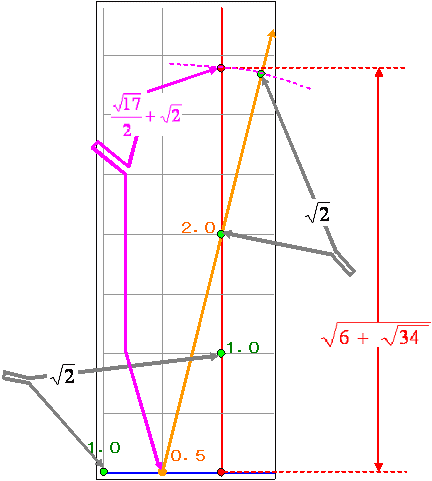
| 偮傑傝丂乮 | 俀 | 亄 | ) | 2 | 亅( | 侾 俀 | ) | 2 | 亖俇亄 |
仧弌戣幰偺僐儊儞僩丅
Y.M.Ojisan 偝傫傊丅
杔偺峫偊偰偄偨傛傝傛偄夝摎偱偡偹丅
捈慄偺悢偊曽偼惓偟偄偱偡丅
偪側傒偵丄偐偊傞偝傫偺嶌恾偺捈慄偺悢偊曽傪杔偑娫堘偊偰偄傑偟偨丅
嵟弶偺35噋偺捈慄丄嵟弶偺墌偐傜堷偄偨悅慄丄俀偮傔偺墌偐傜堷偄偨悅慄偼偄偄偺偱偡偑丄
俀偮傔偺墌傪昤偔偨傔偵拞怱傪掕傔傞昁梫偑偁傝傑偡丅
偦偺拞怱傪掕傔傞偨傔偵偼擇摍暘慄傪巊偆昁梫偑偁傞偺偱崌寁係杮偱偟偨丅
栤戣偺愝掕偱偼1噊扨埵偺掕婯偱嶌恾傪偡傞偲偄偆偙偲偱偟偨偑丄杔偺峫偊偱偼1噋扨埵偺掕婯偱傕嶌恾壜擻偱偡丅
傕偪傠傫丄5噋巐曽偺巻傪梡偄偰偱偡丅
偦偪傜傕峫偊偰傒偰偔偩偝偄丅
栤戣侾傕傛傠偟偔丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂栤戣係 偦偺俀亃
丂挿偝偺嵟彫扨埵偼侾們倣丄巻偺戝偒偝偼俆們倣亊俆們倣埲壓偱丂捈慄偺悢傪嵟彫偵偡傞偙偲傪峫偊傑偟偨丅
寢壥丄捈慄偼俀杮偱偡丅
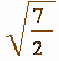 偱偡丅
偱偡丅
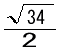 偱偡丅
偱偡丅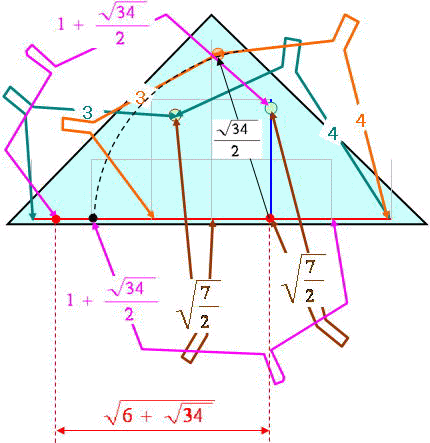
偮傑傝丂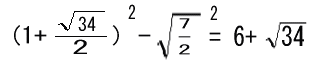 丂偱偡丅
丂偱偡丅
亂僐儊儞僩亃
慜夞偺曽朄偱傕丄傕偆堦杮捈慄傪巊偊偽侽丏俆們倣傪嶌惉偱偒侾們倣扨埵偱傕嶌惉壜擻偱偡丅
偦偙偱崱夞偼丄偝傜偵捈慄傪尭傜偟偰傒傑偟偨丅
偦偺暘僐儞僷僗偑懡梡偝傟丄偁傑傝僗儅乕僩偱偼偁傝傑偣傫偑丅丂
仧弌戣幰偺僐儊儞僩丅
亂Y.M.Ojisan 偝傫偐傜偺夞摎偦偺2偵偮偄偰偺僐儊儞僩亃
杔偑峫偊偰偄偨傛傝傕惁偄夞摎偱偡丅
棟夝偡傞偺傕擄偟偄偱偡丅
偪側傒偵杔偺峫偊偰偄偨摎偊偲尵偆偺偼
6+併34=x,6-併34=y偲偍偄偰
併x亇併y=併(x+y亇2併xy)偲偟偰
x+y=12,xy=2傛傝
併x亇併y=併{32+(併2亇1)2}偲偡傞夞摎偱偡丅
偙傟偱傕5cm亊5cm偱彂偗傞夞摎偱偡丅
Y.M.Ojisan 偝傫側傜偙傟偩偗偱傕嶌恾偱偒傞偱偟傚偆丅
偤傂傗偭偰傒偰偔偩偝偄丅