◆山梨県 Footmark さんからの解答。
【問題1】
∠ADBが∠ACBの半分になることは起き得ません。
【証明】
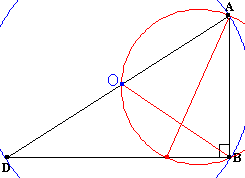
△ABDは∠ABDが直角の直角三角形ですから外心はADの中点Oです。
すると、円周角と中心角の関係より∠ADBは∠AOBの半分です。

そこで、△AOBの外接円を考えると∠AOBは弦ABが張る円周角です。
ですから、、その外接円が点Cを通れば、∠ADBが∠ACBの半分となります。
ところが、点Cも点Oも△ABDの辺の中点です。
よって、中点連結の定理より∠OCDは∠ABCに等しく直角、故に∠OCBも直角です。
また、ADとBDは三角形の2辺のため明らかに平行ではありません。
ですから、∠OABも∠AOCも直角ではありません。
∴ ∠OAB+∠OCB≠2直角 かつ ∠ABC+∠AOC≠2直角
よって、四角形ABCOの外接円は存在せず、
∠ADBが∠ACBの半分になることは起き得ません。
◆宮城県 甘泉法師 さんからの解答。
【問題1】
∠ADC=θとおくと題意の関係は
cotθ=2cot(2θ)となります。
cotθ=xと記し右辺の三角関数を変形し、式は
| x= | x2 -1 x |
x2=x2 -1
0=-1
よって題意の関係は満足できない。
◆東京都 由釜与祢弥 さんからの解答。
【問題1】
存在しない。
条件を満たすとき AC=BC であるが、
∠ACB=0°となり、三角形ABC はもはや三角形ではない。
◆宮城県 甘泉法師 さんからの解答。
【問題2】
∠AEC=θとおくと題意の関係は
3cot(3θ)-cotθ=0
cotθ=xとおき右辺は
3cot(3θ)-cotθ
| = | 3x(x2-3) 3x2-1 | -x |
| = | x{3(x2-3)-(3x2-1)} 3x2-1 |
| = | -8x 3x2-1 |
| 0になるのはx=0つまりθ= | π 2 | だが、これは不適解。 |
よって題意の点Eは存在しない。(終)
【コメント】
より一般化して
| 0<θ< | π 2 | , p>0において |
f(p) = pcot(pθ) - cotθ をpで微分し
f’(p) = cot(pθ) + θ cosec2(pθ)>0
よってf(p)は単調増加
| f(0+)= | 1 θ | -cotθ= | tanθ-θ θtanθ |
>0 |
なので f(p)>0
よって f(p)≠0
◆出題者のコメント。
宮城県 甘泉法師 さんへのコメント
正解です!!
答えてくださってありがとうございます。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題2】
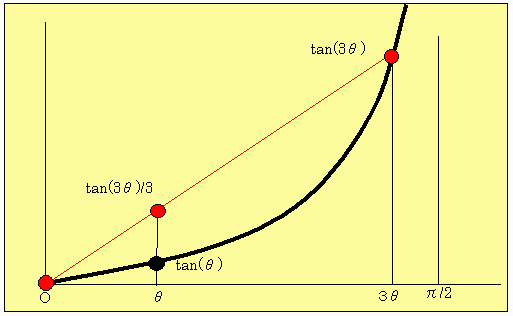
tan(θ)は0〜π/2の範囲で下に凸である。
従ってtan曲線上の2点(原点と3θ)を結ぶ線分はtan曲線の下にはない。
| よって、その | 1 3 | に位置する点(θ, | tan(3θ) 3 | )は |
| つまり、tan(θ)< | tan(3θ) 3 | である。 |
この式は甘泉法師さんのcot(θ)>3cot(3θ)と同じである。
よって、θ=0を除いて解は存在しない。
倍数3が一般に1より大きい実数であっても同じであることは上図より明快である。
◆福岡県 micky さんからの解答。
【問題1】
∠CAB=a ∠ACB=2b ∠CDA=b ∠CAD=c とおくと、
a+2b=90 a+b+c=90 より、a+2b=a+b+cとなり、
2b=b+cとなる。
よって、b=c
だから、CD=CA=CB となるが、これは、直角三角形ABCに矛盾する。
(CA=CB ではない。)
◆石川県の中学校3年生 Moo さんからの解答。
【問題1】
結論;問題の条件を満たす∠ACBは存在しない。
〔証明〕
BC=DCより,直径BD,中心Cである円Pを描くことができる。
∠ABD=90°より点Aは円Pの点Bにおける接線上にあり,また点Bと異なる。…(1)
| ∠ADB= | 1 2 |
∠ACBより点Aは円P上にある。…(2) |
しかし,(1)と(2)を同時に満たす点Aは存在しない。
したがって,問題の条件を満たす点Aをとることはできないので∠ACBは存在しない。
ゆえに,結論が成り立つ。
【問題2】
結論;問題の条件を満たす∠ACBは存在しない。
〔証明〕
∠ACB=3∠AEB=3θ,EB=3CB=3αとおくと
AB=3αtanθ
AB=αtan3θ
と表せる。
| ただし,0<3θ< | π 2 |
より | 2 |
<cosθ<1である。…(1) |
よって、この2式より
3αtanθ=αtan3θ
α>0より,両辺αで割ってから2乗して
9tan2θ=(tan3θ)2
| 9( | 1 cos2θ |
−1)= | 1 (cos3θ)2 |
−1 |
| 9( | 1 cos2θ |
−1)= | 1 {3cosθ−4(cosθ)3}2 |
−1 |
| 9( | 1 cos2θ |
−1)= | 1 9(cosθ)2−24(cosθ)4+16(cosθ)6 |
−1 |
| 9( | 1 β |
−1)= | 1 9β−24β2+16β3 |
−1 |
これを解くと
| β= | 5 8 |
,β=1 |
よって、
| cosθ=± | 4 |
,cosθ=±1 |
しかし、いずれも(1)を満たさない。
したがって、問題の条件を満たすθは存在しない。
ゆえに、結論が成り立つ。