亀崅峑惗偐傜偺挧愴忬Part37亁夝摎
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂栤戣俀亃
摎偊
丂
値杮偺暯柺儀僋僩儖傪倁倠丂倠亖侾乣値丂偲偟傑偡丅
傑偨偦偺廤崌傪俙偲偟傑偡丅
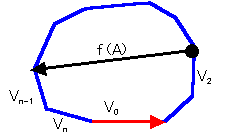
栤戣偼丂忦審丂儼乥倁倠乥亖値丂偺尦丂
f(A)亖max(乥儼倴[v伕俙]乥)傪昡壙偡傞偙偲偱偡丅
俙偵儀僋僩儖倁侽傪捛壛偟丂俙丱偲偟傑偡丅
偨偩偟倁侽偼丂儼倴[v伕俙丱]亖侽丂偱偁傞儀僋僩儖偱偡丅
偝傜偵丄俙丱偺儀僋僩儖傪倁侽偺曃妏傪侽偲偟偰
曃妏乮侽亝arg(倁倠)亙俀兾乯 偺弴偵暲傋懼偊傑偡丅
偙傟傪夵傔偰偦偺弴偵倁倠偲偟傑偡丅
懄偪丂arg(倁倠)亝arg(倁倠亄1)丂倠亖侽乣値偱偡丅
俙丱偺儀僋僩儖傪偦偺斣崋弴偵楢偹偰昤偔偲丄
arg(倁倠)亝arg(倁倠亄1)丂偱偁傞偺偱撌懡妏宍丗俼(A)偑昤偐傟傑偡丅
偦偺撌懡妏宍俼(A)偺擟堄偺俀揰娫偼嵍夞傝塃夞傝偺擇偮偺宱楬偑偁傞偺偱丄倁侽傪梡偄偢俙偺梫慺偺傒偱峔惉偱偒傑偡丅
傑偨丄f(A)偺嵟挿傪梌偊傞儀僋僩儖偺榓傪俽偲偡傞偲偒丄俽傪峔惉偡傞儀僋僩儖偺俽曽岦惉暘偼柧傜偐偵晧偱偼偁傝傑偣傫丅
廬偭偰丄偦傟傜傪曃妏偺弴偵暲傋傟偽俼乮俙乯偺堦晹偲側傝傑偡丅
偮傑傝丄f(A)亖max(R(A)乯偺捀揰娫嫍棧)偱偡丅
偙偙偱彮偟旘桇偟傑偡偑丄掕嬓恾宍乮墌傗儖乕儘亅偺嶰妏宍乯傪峫偊傑偡丅
掕嬓恾宍偱偼廃挿亖兾亊嬓偺娭學偑偁傝傑偡丅廬偭偰
掱搙偲偄偆偙偲偑暘偐傝傑偡丅
摿偵値偑婏悢偺慺場悢傪帩偮偲偒偼
偱偡丅
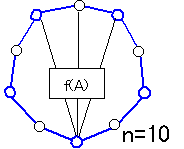
壓恾偼偙偺娭學傪丂値亖侾侽亖俆亊俀丂偺応崌偵梌偊傞俙偱偁偭偰丄儖乕儘亅偺屲妏宍儀乕僗偵嶌惉偟偨偺傕偺偱偡丅
側偍倁侽亖侽偱偡丅
丂
倖乮俙乯偺嵟彫傪梌偊傞俙偵偍偄偰偼丄倁侽亖侽偱偁傞傕偺偑偁傞偙偲偼柧傜偐偱偡丅
傕偟丄倁侽亗侽側傜偽丄倁侽偑侽偵側傞傛偆偵俼乮俙乯偺撪晹偵廃挿偑値偱偁傞撌懡妏宍俼'偑偱偒傞偺偱丄嵟挿懳妏慄偑挿偔側傞偙偲偼側偄偐傜偱偡丅
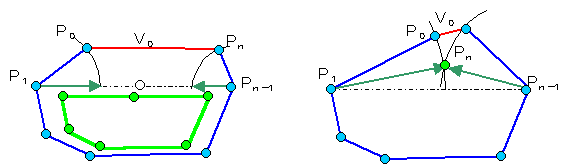
壓恾偵俼'偺嶌傝曽傪帵偟傑偡丅
偨偩偟丄値亞俀偱 巒揰傪俹侽偲偟俹j=Pj-1+倁j偲偟傑偡丅
俹侾偲俹値亅侾傪寢傇慄暘偼俼乮俙乯偺拞偁傝丄偙偺忋偵倁侾偍傛傃倁値偲摨偠挿偝偺儀僋僩儖傪庢偭偨偲偒丄壓嵍恾偺傛偆偵撏偐側偄応崌偲丄塃恾偺傛偆偵撏偔応崌偑偁傝傑偡丅
撏偐側偄応崌偼慄暘俹侾俹値亅侾忋偵怴偨偵俹侽亖俹値傪偲傝丄慡懱傪弅彫偟偰廃挿値偺撌懡妏宍俼'傪嶌惉偱偒傑偡丅
堦曽撏偔応崌偼塃恾偺傛偆偵俼乮俙乯撪偵怴偟偔俹侽亖俹値傪庢傞偙偲偑偱偒廃挿偑値偺撌懡妏宍俼'傪嶌惉偱偒傑偡丅
偙傟傜俼'偺嵟挿慄暘挿偑俼乮俙乯偺偦傟傪挻偊傞帠偼偁傝傑偣傫丅
埲忋傛傝壓婰偺栤戣傪峫偊傟偽傛偄偙偲偑暘偐傝傑偟偨丅
側偍丄値亖侾丄俀偺応崌傕娷傔偰傛偄偱偡偑丄偙偙偱偼彍奜偟傑偡丅
亂栤戣愝掕亃
俙傪廃挿値偺撌値妏宍偲偟丄俙撪偺嵟挿慄暘挿傪倖乮俙乯偲偡傞偲偒丄倖乮俙乯偺壓尷抣傪値偱昞傢偣丅
偨偩偟値亞俁偲偡傞丅
亂曗戣侾亃
俙撪偺嵟挿慄暘挿倖乮俙乯傪梌偊傞慄暘偺椉抂偼俙偺捀揰偱偁傞丅
佹丂捈慄忋偺揰傊偺嫍棧偺惈幙偐傜柧傜偐偱偡丅
徻嵶棯
亂曗戣俀亃
俙偑倖乮俙乯偺壓尷抣傪梌偊傞恾宍偱偁傞偲偒丄俙偺擟堄偺捀揰偐傜偺嵟挿慄暘挿偼
倖乮俙乯亖壓尷抣偵慡偰摍偟偄丅
佹丂攚棟朄偱徹柧偟傑偡丅
堦斒惈傪幐傢偢俹侾傪巒揰偲偡傞擟堄偺儀僋僩儖挿偑f(A)傛傝彫偝偄偲偟傑偡丅
俹俁俹俀偺墑挿偲俹値亅侾俹値偺墑挿偑俙偺奜偵嶌傞椞堟嚈偑壓嵍恾偺傛偆偵懚嵼偟偰偄傟偽丄俹侾偐傜偺嫍棧偑倖乮俙乯偵嬤偯偔傛偆偵俹侾'傪偲傞偙偲偑壜擻偱偁傝丄偙偺偲偒廃挿偼憹戝偟傑偡丅
傛偭偰丄慡懱偵弅彫偟偰廃挿傪値偲偟丄偙傟傪俙'偲偟偨偲偒丄
倖乮俙'乯亙倖乮俙乯偱偁傝丄壓尷抣偱偁傞偙偲偵柕弬偟傑偡丅
壓塃恾偺傛偆偵椞堟嚈偑懚嵼偟側偄応崌偼丄俹俀偲俹値偼曈拞娫偺揰偵側傝傑偡丅
傛偭偰丄曗戣侾偵傛傝俹俀傑偨偼俹値傪巒揰偲偡傞擟堄偺儀僋僩儖挿偼巒揰偑椬偺捀揰偵堦抳偟側偄尷傝丄f(A)傛傝彫偝偄偙偲偑暘偐傝傑偡丅
偦偙偱夵傔偰偙傟傜傪俹侾偲偟偰峫偊偰傕椙偄傢偗偱偡丅
俙偼撌恾宍偱偁傞偺偱丄偙傟傪孞傝曉偟偨偲偟偰傕壗傟偳偙偐偱椞堟嚈偑懚嵼偟丄柕弬偑惗偠傑偡丅
亂曗戣俁亃
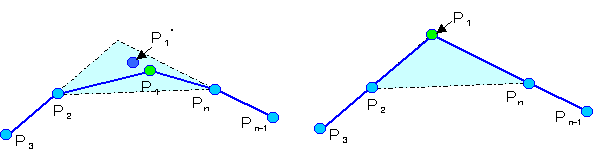
俙偑倖乮俙乯偺壓尷抣傪梌偊傞恾宍偱偁傞偲偒丄
俙偺捀揰俹偲俹侾偍傛傃俹倣偲偺嫍棧偑倖乮俙乯偵摍偟偗傟偽丄
俹偲偦偺娫偺捀揰俹倠[倠亖俀乣倣亅侾]偲偺嫍棧傕倖乮俙乯偵摍偟偔丄傑偨俹娫偲偺傒偵尷傞丅
佹丂傑偢俙偺忦審傛傝丄俹侾偲俹倣偺嫍棧偼倖乮俙乯埲壓偱偁傝丄
傑偨俙偼撌恾宍偱偡偐傜俹倠偺懚嵼斖埻偼丆壓恾搷怓敿寧宍椞堟偱偡丅
俹倠偲俹侾偲俹倣娫偼倖乮俙乯傛傝彫偝偔丄傑偨俹偲傕倖乮俙乯傛傝彫偝偄丅
曗戣俀傛傝俹倠偲偦偺懠偺捀揰娫偱嫍棧偑倖乮俙乯偱偁傞傕偺偑懚嵼偟側偗傟偽側傜偢丄偦偺揰偼壓恾愒慄偺尫忋偵偁傝傑偡丅
偲偙傠偑丄偦偺揰偼俹侾傑偨偼俹倣偐傜倖乮俙乯傛傝戝偒側嫍棧偺揰偲側偭偰偟傑偄傑偡丅
傛偭偰丄俹偲偦偺娫偺捀揰俹倠[倠亖俀乣倣亅侾]偲偺嫍棧偑倖乮俙乯偵側傞偟偐偁傝傑偣傫丅
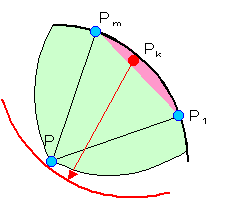
亂曗戣係亃
俙偑倖乮俙乯偺壓尷抣傪梌偊傞恾宍偱偁傝丄
俙偺捀揰俹偲捀揰俹倠[倠亖侾乣倣]偲偺嫍棧偑倖乮俙乯偵摍偟偄偲偒丄
俹倠偼摍娫妘偱偁傞丅
佹俙偺忦審傛傝丄俹侾偲俹倣偺嫍棧偼倖乮俙乯埲壓偱偁傝丄
俹侾偐傜俹倣傑偱偺曈挿偺崌寁偑摍娫妘偺偲偒嵟戝偱偁傞偙偲傪帵偟傑偡丅
偙傟偑帵偝傟傟偽丄摍娫妘偱側偄偲偒丄摍娫妘偵挷惍偡傞偙偲偵傛傝俙偺廃挿偑挿偔側傝丆偦偺暘俙偺慡懱弅彫偑壜擻偲側傝丄倖乮俙乯偑壓尷偱偁傞偙偲偵柕弬偡傞偐傜偱偡丅
側偍曗戣俁偵傛傝俹偲偺傒偺嫍棧偩偗峫偊傟偽椙偄偙偲偑曐徹偝傟偰偄傑偡丅
丂
| 俹傪拞怱偲偟丄俹倠偲俹倠亄侾偺曃妏嵎傪丂侽亙兤倠亝 |
兾
3 | 偲偡傞偲偒 |
| 曈挿偺崌寁亖 |
倣亅侾
儼
倠亖侾 |
俀sin( |
兤倠
俀 |
乯偱偡丅 |
| 侽亙兤 |
倠 |
亙兾丂偵偍偄偰俀sin乮 |
兤倠
俀 |
乯偼忋偵撌偱偡丅 |
廬偭偰偦偺娭悢抣偺暯嬒偼暯嬒偺娭悢抣傛傝彫偝偔丄摍崋偼堷悢偑慡偰摍偟偄応崌偱偡丅懄偪丄
倣亅侾
儼
倠亖侾 |
俀sin( |
兤倠
俀 |
)亝俀乮倣亅侾乯sin乮 |
儲
倣亅侾 | 乯 |
偑惉棫偟傑偡丅傑偨倣摍崋偼丂倠亖侾乣m-1偵懳偟偰丄
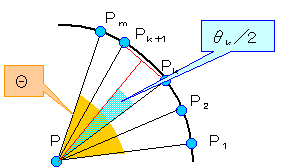
亂曗戣俆亃
壓婰偑惉棫偡傞丅
| 倖乮俙乯 |
亞 |
侾
俀sin(兾乛2n) |
亜 |
値
兾 |
佹丂曗戣俁傛傝俙慡懱偺曃妏嵎兤倠偺榓儲all偼兾偱偡丅丂
傑偨曗戣係偼兤倠偑兾埲壓偲偟偰傕惉棫偡傞曗戣偱偁傞偺偱丄
廃挿偼f(A)亊俀値亊sin(兾乛2値)亖値丂傛傝丂
偱偁傝丄偙傟偑嵟掅抣偱偡丅
亂寢壥侾亃
値亖倫亊俀倯丂丂倫丗俁埲忋偺婏悢丂偱偁傞偲偒丄
| 傕偟兤倠亖 |
兾
値 | 側傞攝抲偑懚嵼偟丄倖乮俙乯偺壓尷抣偼 |
佹儖乕儘亅偺惓婏悢懡妏宍偑懚嵼偡傞偺偱丄儖乕儘亅偺惓倫妏宍傪嶌恾偟丄偦偺捀揰偵慡晹偱倫屄偺捀揰偲丂奺曈拞傎偳偵俀倯亅侾屄偯偮摍娫妘偵捀揰傪攝抲偡傞偙偲偑壜擻偱偡丅
亂寢壥俀亃
値亖俀偺偲偒丂V1+V2=0 偲偟偨応崌偺丂f(A)=1偑嵟彫偱偁傞丅
佹徣棯
亂寢壥俁亃
値亖係偺偲偒丂儖乕儘亅偺3妏宍偺俁捀揰偲堦曈偺拞墰偵攝抲偟偨傕偺偑倖乮俙乯偺嵟彫傪梌偊傞丅
| 倖乮俙乯 |
亖 |
俁
2+1/cos(兾/12) |
=0.988378 |
丄 |
(A)*俀sin( |
兾
2値 |
乯=1.003062 |
佹徣棯
亂寢壥係亃
値亖俉偺偲偒丂儖乕儘亅偺3妏宍偺俁捀揰偲曈偺拞墰俀丄俀丄侾屄攝抲偡傞曽朄偲丄儖乕儘亅偺旕惓俆妏宍偵捀揰傪壓恾偺傛偆偵攝抲偟丄f(A)傪嵟彫壔偟偰傒傑偟偨丅
恀偺倖乮俙乯偺壓尷抣偑徹柧偝傟偨傢偗偱偼偁傝傑偣傫丅
杦偳棟憐偵嬤偔偼側偭偰偄傑偡丅
儖乕儘亅偺俁妏宍儀乕僗偺応崌偼丂
f(A)=2.56488丂丄f(A)*俀sin(兾乛2値)亖1.000766
儖乕儘亅偺俆妏宍儀乕僗偺応崌偼
f(A)=2.56316丂丄f(A)*俀sin(兾乛2値)亖1.000095
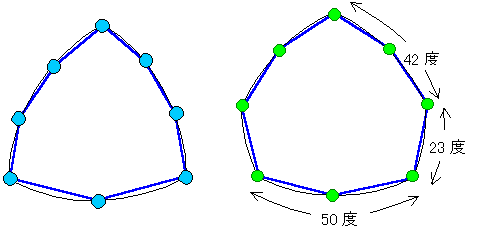
亂寢壥俆亃
値亖俀倯偺偲偒丂
儖乕儘亅偺3妏宍偺俁捀揰偲曈偺拞墰晹偵嵟戝尷捀揰傪摍暘攝偟偨応崌偲丄
寢壥係偱摼偨儖乕儘亅偺旕惓俆妏宍攝暘傪峏偵俀摍暘偟偰偄偭偨応崌偺寁嶼寢壥傪壓昞偵帵偟傑偡丅
値偑戝偒偔側傞偲嶡偟偺捠傝丄儖乕儘亅偺3妏宍儀乕僗偺曽偑棟憐偵嬤偔偼側偭偰偄傑偡丅

亂姶憐亃
栤戣侾偺昡掕偲丄巹偺摼偨寢壥偑堘偆偺偱丄巹偺栤戣偺夝庍側偄偟夝摎偑堘偭偰偄傞偺偐傕偟傟傑偣傫偑丄柺敀偄栤戣偩偲巚偄傑偟偨丅
俀倯偺帪偺姰慡側夝摎偑摼傜傟側偐偭偨偺偱巆擮偱偡丅
丂亀崅峑惗偐傜偺挧愴忬Part37亁傊
丂悢妛偺晹壆傊傕偳傞








