◆愛知県 Y.M.Ojisan さんからの解答。
【解答】
Nが 3の倍数か3の倍数+1であること。
【証明】
1。と2。の手順があるのは面倒なので、最初に1個ダミーの白点を加え、リングにします。
すると、1。の手順は2。の手順に含まれます。
また、このとき、両側の点の色をつねに反転させるので、リング全体の黒点の数はつねに偶数です。
従って、ダミー点以外が全部白になったとき、ダミー点も白です。
なお1。の手順により枝を出すことも可能ですが、2度と一直線にはできないので枝分かれを考える必要はありません。
つまり、最初2個の白点が輪に繋がっている状態から 2。のみのルールで全部白にできるリングの点の総数 m=N+1 の条件を求めればよいです。
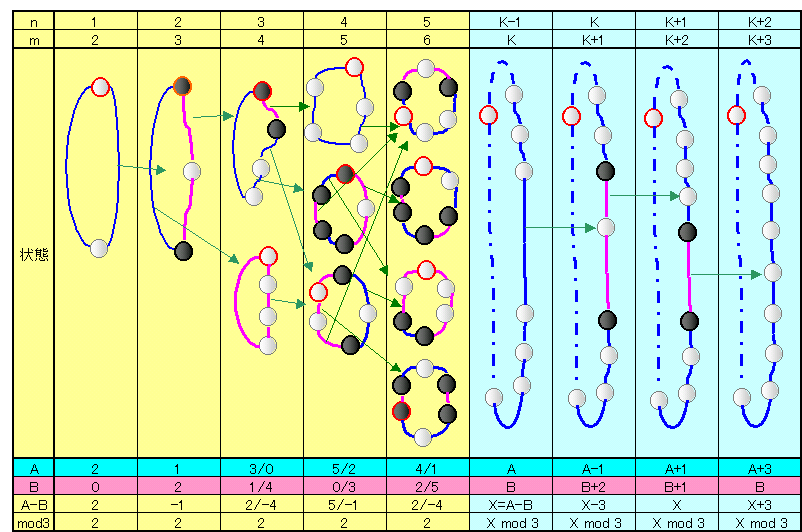
下図に示すように、mが2、4、5の時は可能で、3、6の時は不可能です。
また、m=Kが可能であればm=K+3も可能です。
従って、少なくともmが3の倍数でないとき可能です。
以下、mが3の倍数のとき不可能であることを示します。
先に示したように黒点の数は偶数です。
従って、黒点間の区間の数も偶数です。
そこで 偶数番目区間の総長さAと、奇数番目区間の総長さBの差を考えます。
すると、下図に示されているように2。の操作を黒点間に加えようと、白点間に加えようと、白黒間に加えようと3を法とするA−Bの剰余値は常に2です。
一方、mが3の倍数のとき全部白になれば
|A−B|=m≡0 mod 3 ですから2ではありません。
よって、mが3の倍数のときは全部白にすることは不可能です。

【感想】
たしかに、試験に出たら無理でしたね。
アイデア一発ですが、1時間ではアイデアは出なかった。
気分転換というか切羽詰ってトイレに行ったら出ました。^^
◆山梨県 Footmark さんからの解答。
1直線上の黒点は、1直線上にない新たな点と1の操作をすれば白点にできるので、「1点もしくは枝別れのない棒状グラフ」でないと、1直線上に並ぶ白点は何個でも可能です。
よって、「1点もしくは棒状グラフ」という条件があるものとします。
【答え】
Nは、3の倍数か3で割ると1余る。
【証明】
便宜的に、白点を○で黒点を●で表し、両端だけに点を持つ線分を「辺」と呼ぶものとする。
また、1の操作は点を選ぶので「点操作」、2の操作は辺を選ぶので「辺操作」と呼ぶものとする。
【操作をしないとき】
白点の個数Nは1だが、1は明らかに3で割ると1余る。
【操作をするとき】
下は、右端の点に点操作をしてから、ある特定の辺(=)に辺操作をしたときと、ある特定な辺(=)に辺操作をしてから、右端の点に点操作をしたときの、比較である。
元のグラフ 点操作後のグラフ 辺操作後のグラフ ……元=元……元 ……元=元……逆ー○ ……逆ー○ー逆……逆ー○ ……元=元 ……元=逆ー○ ……逆ー○ー元ー○ 元のグラフ 辺操作後のグラフ 点操作後のグラフ ……元=元……元 ……逆ー○ー逆……元 ……逆ー○ー逆……逆ー○ ……元=元 ……逆ー○ー逆 ……逆ー○ー元ー○明らかに、点操作と辺操作の順序を入れ替えても結果は同じである。
ところで、点操作は明らかにグラフの端の点に対してしかできないが、グラフの片端だけにする場合と、グラフの両端にする場合が考えられる。
以下、Mを正整数、L,Rを非負整数とする。
【A】グラフの片端だけに点操作をする場合
まず、片端だけに点操作を何回か繰り返すと、
必ず (●……)●ー○ か ○ー●(……●) になる。
辺操作は両端が●である辺を選ぶので、全点操作終了時点では●は偶数(2M)個でなければならないが、明らかに、グラフの片端の点に2M回点操作をすれば実現できる。
次に、グラフの端に1番近い両端が●である辺に対し、M回辺操作をすれば2M個の●は3M個の○に変わる。
すると、最初から○だった1つを加えると、○の個数Nは3M+1となる。
3M+1は、明らかに3で割ると1余る。
【B】グラフの両端に点操作をする場合
まず、両端に点操作を何回か繰り返すと、
必ず ○ー{(●……)●ー}○{ー●(……●)}ー○ になる。
全点操作終了時点では、左側の●も偶数(2L)個、右側の●も遇数(2R)個でなければならないが、
明らかに、グラフの左端の点に(2L+1)回、右端の点に(2R+1)回点操作をすれば実現できる。
次に、グラフのそれぞれの端に1番近い両端が●である辺に対し、
合計(L+R)回辺操作をすれば2(L+R)個の●は3(L+R)個の○に変わる。
すると、最初から○だった3つを加えると、○の個数Nは3(L+R)+3個となる。
3(L+R)+3は、明らかに3の倍数である。
証明終わり。
◆東京都 昔とった杵柄 さんからの解答。
答えは、「Nを3で割った余りが、0と1の時は可能で、2の時は不可能。」です。
N=3M+1と、3Mの時に可能なのは、Footmarkさんと同様です。
以下、N=3M+2の時には、真っ白にはできない事を証明します。
【証明】
1) オイラー数のような物の定義
白丸と黒丸の図形に対して、左から何番目の位置に黒があるかを考えて、その数字を、大きい順に並べて、交互に足して引いた数を作り、
それを mod3 で見た数を、オイラー数(のような物)と定義します。
例えば、「○●○○●●」という図形だったら、
左から、6、5、2番目に黒があるので、
+6-5+2 = 3 = 0 (mod3)となります。
2) オイラー数のような物の性質
問題にある操作のうち、一番左に○を付ける操作と、中間に割り込ませる操作では、オイラー数(のような物)は 1減少(mod3)します。
例えば、左端に○を付ける操作の場合、
左端が○で、その右側に●が偶数個ある場合は、
「○…(●が偶数個)…」が、「○●…(●が偶数個)…」となり、
●が偶数個の部分は、交互に足して引くので、±0
増えた●は、大きい方から奇数番目に当たるので、+2
合計、+2 = -1 (mod3) になります。
実は、私は、全部のパターンについて証明する事を考えていたのですが、Y.M.Ojisanさんの図にあるように、黒丸間の距離の合計だと思えば、当たり前ですね…。
3) その結果
初石に対して、その左側だけに操作する事を考えると、
【コメント】
私の場合は、もしかして、N=11 ぐらいは出来るのでは?と、考えてを捨てきれずに、パソコンで全通り(N=11,14,17,20に対して)検索してしまいました。
やっぱり、テストで出たら、絶対アウトですね。
◆愛知県 Y.M.Ojisan さんからのコメント。
Footmarkさんの解答で 特に
「全点操作終了時点では、左側の●も偶数(2L)個、右側の●も遇数(2R)個でなければならない」
のところがどうしてもトレースできません。
必要条件の方<。。ならない>に付いて、さらに解説をお願いいたしたく思います。
◆山梨県 Footmark さんからの解答。
「左側の●の個数も右側の●の個数も偶数でなければならない」と、するのは誤りで、証明も必要十分ではなく、不十分でした。m(_ _)m
よって、解答を改めました。
1直線上の黒点は、1直線上にない新たな点と1の操作をすれば白点にできるので、
「1点もしくは枝別れのない棒状グラフ」でないと、1直線上に並ぶ白点は何個でも可能です。
よって、「1点もしくは棒状グラフ」という条件があるものとします。
【答え】
Nは、3の倍数か3で割ると1余る。
【証明】
便宜的に、白点を○で黒点を●で表し、両端だけに点を持つ線分を「辺」と呼ぶものとする。
また、1の操作は点を選ぶので「点操作」、2の操作は辺を選ぶので「辺操作」と呼ぶものとする。
【操作をしないとき】
白点の個数Nは1だが、1は明らかに3で割ると1余る。
【操作をするとき】
下は、右端の点に点操作をしてから、ある特定の辺(=)に辺操作をしたときと、ある特定な辺(=)に辺操作をしてから、右端の点に点操作をしたときの、 比較である。
元のグラフ 点操作後のグラフ 辺操作後のグラフ ……元=元……元 ……元=元……逆ー○ ……逆ー○ー逆……逆ー○ ……元=元 ……元=逆ー○ ……逆ー○ー元ー○ 元のグラフ 辺操作後のグラフ 点操作後のグラフ ……元=元……元 ……逆ー○ー逆……元 ……逆ー○ー逆……逆ー○ ……元=元 ……逆ー○ー逆 ……逆ー○ー元ー○明らかに、点操作と辺操作の順序を入れ替えても結果は同じである。
また、どのような辺操作をしても、下のように●の総個数の偶奇は明らかに変わらない。
…●ー●… → …○ー○ー○… …●ー○… → …○ー○ー●… …○ー●… → …●ー○ー○… …○ー○… → …●ー○ー●…よって、●の個数を0(偶数)個にするには、全点操作終了時点で既に●の総個数が偶数でなければならない。
ところで、点操作は明らかにグラフの端の点に対してしかできないが、グラフの片端だけにする場合と、グラフの両端にする場合が考えられる。
以下、Mを正整数、L,R,L',R'を非負整数とする。
【A】グラフの片端だけに点操作をする場合
片端だけに点操作を何回か繰り返すと、
必ず (●……)●ー○ か ○ー●(……●) になる。
ところで、全点操作終了時点では●の総個数は偶数でなければならないが、
●の個数を2M個にするには、グラフの片端の点に2M回点操作をすれば実現できる。
この後、グラフの端に1番近い両端が●の辺に対し、M回辺操作をすれば2M個の●は3M個の○に変わる。
すると、最初から○だった1つを加えると、○の個数Nは3M+1となる。
3M+1は、明らかに3で割ると1余る。
【B】グラフの両端に点操作をする場合
両端に点操作を何回か繰り返すと、
必ず ○ー{(●……)●ー}○{ー●(……●)}ー○ になる。
全点操作終了時点で、左側の●の個数をL個、右側の●の個数をR個にするには、グラフの左端の点に(L+1)回、右端の点に(R+1)回点操作をすれば実現できる。
ところで、全点操作終了時点では(L+R)は偶数ゆえ、LとRは共に偶数か共に奇数のいずれかである。
共に偶数なら、L=2L'、R=2R' とすると、
グラフの左端に1番近い両端が●の辺に対しL'回、
グラフの右端に1番近い両端が●の辺に対しR'回、
辺操作をすれば、2(L'+R')個の●は3(L'+R')個の○に変わる。
すると、最初から○だった3つを加えると、○の個数Nは3(L'+R')+3個となる。
3(L'+R')+3は、明らかに3の倍数である。
共に奇数なら、中央の○を持つどちらか一方の辺に対し、辺操作をすれば、○が1つ増え、連続した●の個数はいずれも偶数となる。
このとき、左側の●の個数を2L'個、右側の●の個数を2R'個とすると、
グラフの左端に1番近い両端が●の辺に対しL'回、
グラフの右端に1番近い両端が●の辺に対しR'回、
辺操作をすれば、2(L'+R')個の●は3(L'+R')個の○に変わる。
すると、最初から○だった4つを加えると、○の個数Nは3(L'+R')+4個となる。
3(L'+R')+4は、明らかに3で割ると1余る。
【Nを3で割ったとき、2余ることはない証明】
計算できるように、
●をx軸に対称移動の行列![]()
○をー2π/3回転の行列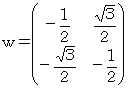
とすると、
下に示すように、どのような辺操作も操作前の行列と操作後の行列は等しい。
●ー● → ○ー○ー○ : bb=www ●ー○ → ○ー○ー● : bw=wwb ○ー● → ●ー○ー○ : wb=bww ○ー○ → ●ー○ー● : ww=bwbつまり、左辺の行列を右辺の行列に置き換えても変わらない。
もし、Nは3で割って2余るなら、wwwが単位行列ゆえ、ww…wはwwと等しい筈である。
そこで、全点操作終了時点で起こり得るすべての状態を考えてみる。
bb…bwまたはwb…bbは、bbが単位行列ゆえ、
bが偶数個ならwとなり、bが奇数個ならbwまたはwbとなり、wwとはならない。
wb…bwb…bwは、bbが単位行列ゆえ、
wbwbw=w,wwbw=wb,wbww=bw,www(単位行列)のいずれかとなり、wwとはならない。
よって、Nを3で割って2余ることはあり得ない。
証明終わり。