『高校生からの挑戦状Part27』解答

◆東京都　鳥居 さんからの解答。

答えから示すと、いかなる n に対しても題意を満たすように点を配置することが可能である。
その具体的な方法を示す。



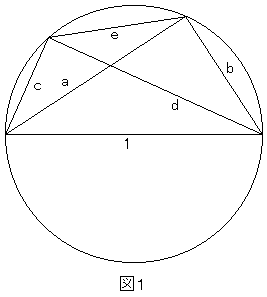
直径 1 の円を描き、その円周上に点を取り、その点と直径の両端を結ぶ線分を a,b とする。
さらに、その円周上に別の点を取り、その新たに取った点と直径の両端を結ぶ線分を c,d とする。
a,b がなす角度と c,d がなす角度はともに直角であるから、以下が成り立つ。
a²＋b²＝1, c²＋d²＝1
(線分 a の長さをそのまま a と表記しています。他の記号についても同様です。)
このとき、a,b や c,d の長さをともに有理数にする点の取り方が無限に存在する。
(後で証明)

ここで、円周上に取った２点間の線分を e とする。
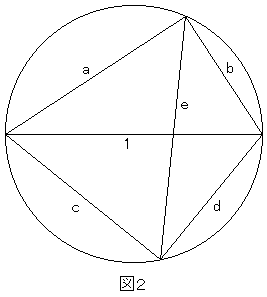
円周上の２点の取り方は、直径で円を２分割したとして、図１のように１つの半円上に２点取る方法と、図２のように２つの半円上に１点ずつ取る方法の２通りある。
まず図１において、e の長さを求めてみる。

a,c がなす角度と b,d がなす角度は等しく、この角度を θ とすると、余弦定理より以下が成り立つ。
e²＝a²＋c²−2ac cosθ＝b²＋d²−2bd cosθ

ここから cosθ を消去すると、
(ac−bd)e²＝ac(b²＋d²)−bd(a²＋c²)

ac−bd を両辺にかけると、
(ac−bd)²e²＝a²c²(b²＋d²)＋b²d²(a²＋c²)−abcd(a²＋b²＋c²＋d²)

a²＋b²＝1, c²＋d²＝1 を使うと、
(ac−bd)²e²＝a²b²＋c²d²−2abcd＝(ab−cd)²
となるから、

e＝±	ab−cd ac−bd

が得られる。
a,b,c,d が有理数であるから、e も有理数となる。

次に図２の場合を扱う。
a,c がなす角度を θ とすると、b,d がなす角度は π−θ となる。
よって、余弦定理から以下が成り立つ。
e²＝a²＋c²−2ac cosθ＝b²＋d²＋2bd cosθ

これは先ほどの式において、d を −d に置き換えたものに等しいから、同様の議論によって、e は有理数といえる。
以上より、図１、図２いずれの場合も円周上の２点間の距離は有理数であることが示される。

直径の両端からの距離がともに有理数となるような円周上の点の取り方は無限にあり、その任意の２点間の距離は有理数である。
それらの有理数の分母をすべて 1 にするように図形を拡大すると、任意の２点間の距離を整数にすることができる。
また、この配置方法に従うと、任意の３点が直線に並ぶこともありません。

「a²＋b²＝1 を満たす有理数 a,b は無限に存在する」の証明
x＝p²−q², y＝2pq, z＝p²＋q² (p,q は整数; p,q,p−q＞0)とおく。
すると、x²＋y²＝z² (x,y,z は整数; x,y,z＞0) が成り立つ。

ここで、以下の条件を課す。

[*] p,q は片方が奇数で他方が偶数、p,q は互いに素。

この条件下では、x＝(p−q)(p＋q) に着目すると、p±q は奇数で、p とも q とも互いに素となることから、x は奇数で、x と y とは互いに素といえる。
x と y が互いに素であれば、x と z も互いに素、y と z も互いに素である。
また、2p²＝z＋x, 2q²＝z−x のように x,z から一意に p,q (p,q＞0) を決められるから、異なる p,q の組から、同じ x,y,z の組を与えることはない。
よって、[*]の条件下では１つの p,q の組から、互いに素である x,y,z の組が１つ生成され、x,y,z の組は重複しないことがいえる。
a＝x／z, b＝y／z とおくと、[*]を満たす１つの p,q の組から、互いに重複しない a,b の組が１つ生成されることになる。

[*]を満たす p,q は無限にあるから、a²＋b²＝1 の下で a,b がともに有理数になる組が無限に存在することが示される。

この問題も手の付けどころに悩みました。
「円上において有理点が１つでもあれば、その円上には有理点が無限にある」ということをヒントにして解いてみました。
これ以外の配置方法があるか？他に寄せられる解答も楽しみです。

◆岩手県　高梨 さんからの解答。

【補題】

sinθ、cosθが共に有理数となる角θ(0＜θ＜π)は無限に存在する

n²+2n+1=(n+1)²

この式に奇数の平方数pをとり、2n+1=pとしてやると上記の条件を満たすθが二つとれる。

例えばp=9のとき、2n+1=9、n=4、√(2n+1)=3より、
4²+3²=5²。

この3数(3,4,5)を辺の長さとする三角形は直角三角形で、直角でない二角は上記の条件を満たす。

同様に、p=25の時(5,12,13)、p=49の時(7,24,25)……と同様の三角形が無限に作成できるが、これらの三角形は「斜辺とそうでない辺の一方との長さの差が1」という条件を必ず満たすので、どの二つをとっても相似になることはなく、ゆえに角の大きさも全て異なる。

【本題】

任意のnに対して、題意を満たす点の配置が可能である。

与えられたnに対して、sinθ、cosθが共に有理数となる角をn個取り、
(θ₁,θ₂,θ₃,…,θ_n)とする。

これらの各θ_iに対して、点(cos2θ_i,sin2θ_i)を取ると、n個の点が原点を中心とした半径1の円上に並ぶ。

これらから任意の二点(cos2θ_i,sin2θ_i)(cos2θ_k,sin2θ_k)を選ぶと、二点間の距離は、
（二点と原点を結ぶ二等辺三角形、原点から底辺に垂線を下ろした図より）

2|sin(θ_i-θ_k)|=2|sinθ_icosθ_k-cosθ_isinθ_k|

となり、これは明らかに有理数。

よってこの方法で取ったn個の点のどの二点を取ってもその間の距離は有理数。

また、明らかに、どの三点を取っても同一直線上に並んではいない。
これらの有理数を分数表記したときの分母の最小公倍数で図を拡大すれば、題意を満たすn個の点の配置が得られる。

【感想】

最初に考えた方向性が、

　sinθ、cosθが共に有理数になるθをとる
⇒二点(cos2θ,sin2θ)(cos4θ,sin4θ)の距離は有理数
⇒一般化して、二点(cos2iθ,sin2iθ)(cos2kθ,sin2kθ)の距離も有理数
⇒点(cos2iθ,sin2iθ)はいくつ取れる？
⇒θがπの有理数倍なら、2θ=(p/q)*2πとして、q個点を取ったらひと巡り
⇒θがπの無理数倍なら……無限に取れる！
⇒「sinθ、cosθが共に有理数でθ=kπ(kは無理数)と表せるθ」がひとつ見つかれば勝利！

という感じだったのですが、「θ=kπ(kは無理数)って何さ？」と出だしで急停止……（’’；。

前半だけ残してθを無限に見つける方向で考えてみたら一瞬でした。

「同一直線上に三点禁止」を無視できるよう、円上配置を思いつくまでが最大のハードルだったかもしれません。

　『高校生からの挑戦状Part27』へ

　数学の部屋へもどる