◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
問題を言い換えると、 GCD(a,b)=GCD(a-2,b-2)=1を満たす2整数a,bから
演算 x♀y=x2-yにより全ての整数を生成可能であるということである。
以下すべて整数において考える。
(補題1)
GCD(α,β,γ)=1であるとき、
∃(l,m,n)があって 1を 1=lα+mβ+nγで表わすことが可能である。
∵互除法により最終的に1が残ることと補題1は等価である。詳細略
(補題2)
e、f、y∈Sのとき {x|x≡y mod |e2−f2|}⊂S
∵e♀(f♀y)=y+(e2−f2) 、
f♀(e♀y)=y−(e2−f2)である。
従って数学的帰納法により
x≡y mod |e2−f2| であるxを全て作ることが可能である。
(本題)
p=a♀b q=b♀a とおく。
また、
α=a2-b2
β=p2-b2=a2(a2-2b)
γ=q2-a2 b2(b2-2a) とする。
このとき、補題2により
y∈Sなら ∀(l,m,n)に対して y+α*l+β*m+γ*n∈Sである。
また、もし GCD(α,β,γ)=1であれば補題1により y±1∈Sである。
少なくともa∈Sが存在しているから、数学的に帰納法によりS=整数全体である。
以下 GCD(α,β,γ)=1を証明する。
まず、GCD(a±b,a)= GCD(±b,a)=1であるから
GCD(α、β)=GCD(α, (a2-2b))である。
なお α=(a-b)(a+b)を利用した。
次に、
GCD(a-b, a2-2b)
=GCD(a-b,a*(a-2))
=GCD(a-b,a-2)
=GCD(b-2,a-2)=1である。
従って、
GCD(α、β)
=GCD(a+b, a2-2b)
=GCD(a+b,a(a+2))
= GCD(a+b,a+2)
= GCD(a+b,b-2)である。
同様にGCD(α、γ)= GCD(a+b,a-2)である。
よって
GCD(α,β,γ)
=GCD(a+b.a-2,b-2)
=GCD(a+b,GCD(b-2,a-2))
=1
【感想】
不思議なくらい過不足無く、巧妙に組み建てられてありますね。
【問題2】
ここでは問題にさらに、次の条件を加えて考える。
(1)平均が定義できることから、f(x)は任意の有界領域で有界である。
(2)f(x)は単写である。
任意の点A,Bを選びa=f(A),b=f(B)とする。
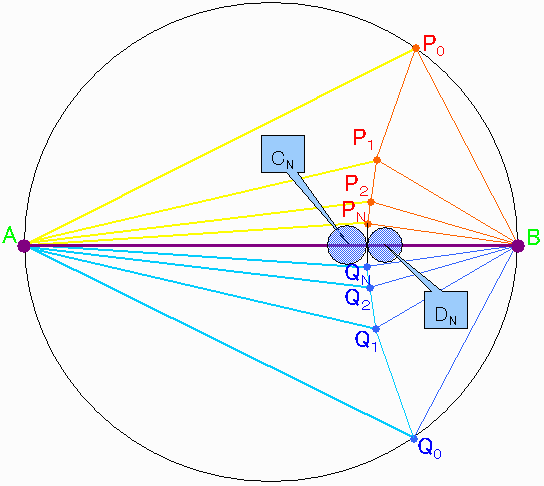
またA,Bを直径とする円周上に2点P0,Q0をとる。
ただし、P0,Q0は直径ABを挟んで対称点である。
なおp=f(P0),q=f(Q0)とする。
一般にi=0〜に対して、△PiABの内心をPi+1とする。
同様に、△QiABの内心をQi+1とする。
また、△APNQNの内心をCN、△BPNQNの内心をDNとする。
対称性からCN、DNは直径AB上である。
| fの定義から f(Pi)= | a+b+f(Pi-1) 3 |
これより
| f(PN)= | a+b 2 | *(1-3-N)+p*3-N= | a+b 2 | +(p- | a+b 2 | )*3-N |
| 同様に f(QN)= | a+b 2 | +(q- | a+b 2 | )*3-N |
またfの定義から
| f(CN)= | a+f(PN)+f(QN) 3 | = | 2a+b 3 | +((q+p)-(a+b))*3-N-1 |
同様に
| f(DN)= | b+f(PN)+f(QN) 3 | = | a+2b 3 | +((q+p)-(a+b))*3-N-1である。 |
従って p,q,a,bは有界値なのでN→∞において
| f(CN)→ | 2a+b 3 | ,f(DN)→ | a+2b 3 | である。 |
ところで、 P0の位置によりC∞点D∞点は直径AB上の全ての位置を取ることが可能である。
fは単写であるので
| f(C∞)=f(D∞)= | 2a+b 3 | = | a+2b 3 | でなければならない。 |

下図は説明に使おうと作成したのですが、とりあえず挿絵です。
