◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
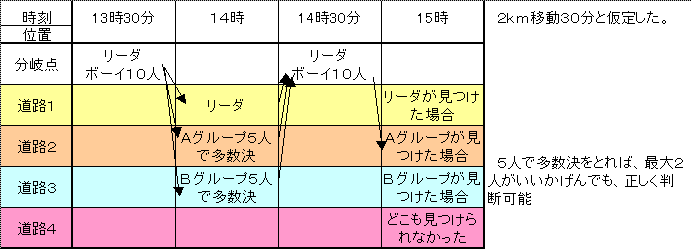
下図のように行動する。

【問題2】
下図のように行動する。
7人を残すことができる。
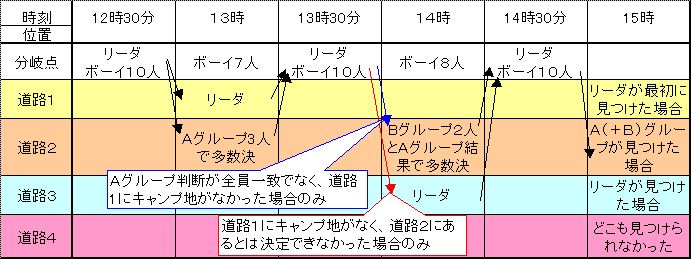
∵ ボーイスカウトは多数決を用いれば5人で1人前です。
探索のために1道路につき2往復できる時間があるので、2.5人ずつ往復できれば良いが、そういうわけには行かないので3人は探索に出かける必要があります。
ボーイスカウトグループはややこしいことを言わずに5人の情報が集まってから多数決すれば良いのですが、そこは省エネ時代ですから少しこだわってみました。
まず、2人先行か3人先行かという選択枝がありますが、2人の情報では2人ともいいかげんの可能性が有りますから、有効な情報にはなりません。
一方3人ならば必ず最低1人は頼れるのがいますから、全員一致の場合のみその結論が有効で、あと2人行く必要が無くなります。(省エネ)
結論が一致しない場合、Aグループはいいかげんなボーイが1人(A)か2人(B)です。
(A)の場合 Aグループの多数決結果は正しいですから、Bグループにもう1人がいても, Aグループ結果を1票として加えて多数決で正しい結論になります。
(B)の場合、Bグループは2人とも頼れるのでAの多数決結果によらずBグループでの多数決結果は正しいです。
(A全員の状態3bitを伝えなくても、或いは票数状態2bitを伝えなくても、A結論の1bit伝えればよいので省情報)
◆出題者のコメント。
見事な解です。もちろん正解です。
AグループとBグループが別の人間だと言うのがポイントですね。
もうひとつ問題3を追加します。
◆愛知県 Y.M.Ojisan さんからの解答。
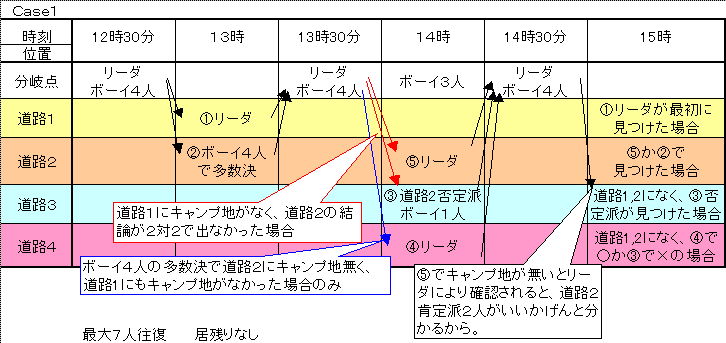
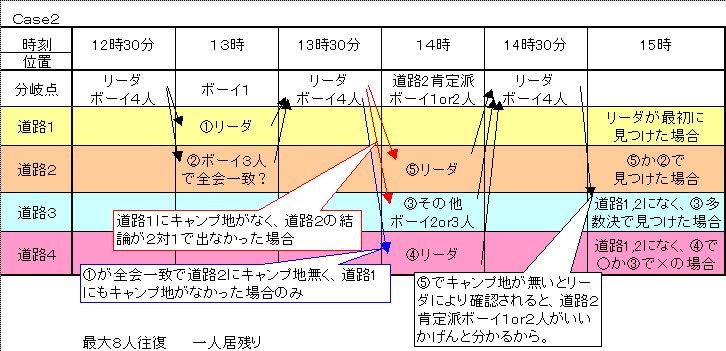
【問題3】
下記2ケースが考えられる。
問題2の条件を入れればケース2。
最悪事の省エネを考えれば、ケース1。
【感想】
これはいい問題です。
問題1と問題2を4人にすればBestSetですね。
問題2の時は気がつきませんでしたが、解答はCase2でもよかったのですね。
◆出題者のコメント。
私が考えていた正解はケース1のほうでした。
ケース2のほうももちろん正解です。