◆東京都 eiki さんからの解答。
【問題4】の答
数学的な解としては...
底面を底面とする4角錐、上面を底面とする4角錐、残りに分ける。
オシマイ。
人間的な解としては...
例えば道場が自分の分を切ることにする
包丁を真ん中に入れようとしたら
坂井「そりゃ半分だ」
陳 「そうだそうだ」
道場「わしもそう思う、こりゃ甘かった」
そこで道場が包丁を少しずつ右側にずらしはじめる
道場「このへんか」
坂井「まだ多いだろう」
陳 「うん、まだ多い」
道場「まだ甘いか」
さらに道場が少しずつ右側にずらし1/3あたりにもっていく
道場「わしはこのへんだと思う」
坂井「まだ多いだろう」
陳 「うん、まだ多い」
道場「じゃあ、わしはこっちはいらん。左側にする」
といって道場は坂井に包丁を渡し、今度は坂井がさらに少しずつ右側にずらす
坂井「このへんだと思う」
陳 「うん、まだ多い」
道場「じゃあ、そこで切ってそれを陳にやりなさい」
坂井「はあ」
道場「残った左側をわしが半分に切る」
坂井「はあはあ」
道場「キミは好きなほうを取りなさい」
オシマイ。
もし道場が包丁を少しずつ右側にずらしはじめたところで
道場「このへんか」という前に、例えば坂井が
坂井「そのへんじゃないですか」
といったとしても、役目を変えれば同じことになります。
要するに半分から少しずつずらしていくことによって
「まだ多い」が3人 --> さらにずらす
「まだ多い」が2人 --> さらにずらす
「まだ多い」が1人
という状態を作ればいいということです。
(少し説明不足の感がありますが、考え方は伝わったかと..)
◆静岡県 ヨッシー さんからの解答。
【問題4】とりあえずこれから。
カステラを長方形とする。
まず道場が縦方向に自分がどれをとっても文句の無いように3等分する
(A,B,Cとする)。
切ったものを、元の長方形にして、坂井が横方向に自分がどれをとっても文句の無いように3等分する
(A1,A2,A3,B1,B2,B3,C1,C2,C3とする)。
次に陳が、各列各行から1個ずつになるように自分の好きな3個を取る。
(A1,B2,C3 A1,B3,C2 など)
たとえば、陳が A1,B2,C3 を取ったとすると、
(A2,B3,C1)(A3,B1,C2)を道場と坂井とで分けるが、どちらがどちらを取っても、文句が出るはずがない。
【問題1】
ヒントの通り。
【問題2】
2人で分ける場合
A,Bの2人で分けて1つ余った場合、すでにもらっている栗の数が奇数ならA,偶数ならBがもらう。
実際には、B,A,A,B,B,A,A,B・・・の順に取っていく。
◆千葉県 fyoshiki さんからの解答。
問2の解答はヨッシーさんに準ずる。
【問題3】
4人をそれぞれa,b,c,dとする。
4人をまず2つのグループA,Bに分ける。
公平に分けるために甘栗の余りが
1個のときA=(a,b),B=(c,d)
2個のときA=(a,c),B=(b,d)
3個のときA=(a,d),B=(b,c)とグループ分けをする。
後は問2のようにA,Bに甘栗を公平に分け、グループ内でも公平に分ければよい。
感想
おそらくグループ分けは任意でもよいような気がするが念のため上のようにしました。
グループ分けが任意なら一般のN人の分配もできるんですが。
(N=2m+1の時は容易。N=2mのときは2つのグループに分ければよい。)
甘栗の分け方が公平であればグループの分け方は任意でもよさそうだけどなぁ。
◆京都府 釜坂 正芳 さんからの解答。
【問題4】
「ケーキを2人で公平に分けるにはどうすればよいか」という問題は昔からありました。
答えは,「一方が真ん中と思うところで切り,もう一人が好きな方を取る」というのが一般に知られている方法です。
しかし,この方法では,3人の場合へは,拡張できません。
そこで,似ていますが,次のように考えます。
A,B二人が同時に真ん中だと思う点(それぞれa点,b点とする)を指し示します。
仮に,aがbより左の場合を考えます。
●aで切ったとき・・・
Aは左を取って丁度半分貰ったと,「納得」
Bは右を取って半分より多く貰ったと思い「ラッキー」
●bで切ったとき・・・
Aは左を取って半分より多く貰ったと思い「ラッキー」
Bは右を取って丁度半分貰ったと,「納得」
つまり,どちらで切っても,Aが左,Bが右を取れば,「損をした」とは思わない。
aで切るか,bで切るかは,さいころでも振って決めるか,第三者に決定して貰えばよいでしょう。
面白いことに相手の主張を受け入れた方が得だと思えるので「譲り合いの喧嘩」が起きそうですので・・・(爆)
実は,二人の場合は,本質的には最初の答えと同じで,最初の場合も,「あとで選ぶ役」を希望して,「ケーキを切る役」にはなりたくないでしょう。
「ケーキを切る役」は絶対に「得をした気分」を味わえないわけですから。
「もっと得をできたのに・・・」と欲たましい事を考えると,問題は成立しませんので,[公平]と言う言葉を[誰もが「損をしていない」と思う]と,解釈して話を進めます。
いよいよ,問題の3人の場合ですが,左から3分の1だと思う点を指し示します。
一番左の点を指した人がその点から左を取り,「納得」します。
あとの2人は残りは3分の2より多いと思い,「ラッキー」となります。
あとは,2人の時の分け方。
N人になっても,N分の1だと思う点を示して,一番左の点を示した人がそこより左を取って,残りを(N-1)人でわけるということを繰り返して分けることができます。
(精密に測定すれば,同じ点を指し示すことはあり得ないし,仮にそうなって,2人または3人のうちの誰が取ったとしても,「損をした」とは思わない。)
【問題1】【問題2】【問題3】について
この場合の[公平]について考えてみました。
結果は,均等ではない。喜ぶ人,がっかりする人がでる。
それでも,全員が納得するする方法ということですよね。
また,実際に”ヨッシーさん”のBAABBAAB・・・という方法で,ちっちゃな子供2人に分けようとしたら,絶対に喧嘩になりますよね。
2人とも先に取りたがるでしょうね。
つまり,甘栗の分配における[公平]とは,[ある程度数学の素養がある人が公平だと感じる]分け方ということになります。
当事者の感情を無視すれば,[全員の期待値が等しくなる]分け方ということになります。
みもふたもないようですが,「じゃんけん」でも「アミダ」でも「サイコロ」でも何でも良いことになります。
それを甘栗の個数(剰余)のみで同じ効果をだすというところが妙味だと思います。
”ヨッシーさん””fyoshikiさん”に拍手。
問題文に,「じゃんけんや他の道具を用いないで・・・」等の但し書きがあったほうがよいと思います。
※2種類の問題で,
問1〜3は,結果は不平等なのに数学的には公平であり,
問4は,数学的には等分しているわけではないのに当事者は納得しているのが面白いと思いました。
あるメルマガの記事を思い出しました。
姉と弟で30個のアメを[公平]に分けるには?
15個ずつ。当たり前すぎ。
年齢で比例配分,身長で比例配分,体重で比例配分・・・
[公平]とか[平等]とかは、むずかしいですね。
◆東京都 合屋 さんからのコメント。
【問題2】【問題3】は”ヨッシーさん””fyoshikiさん”の解答で良いのですが、一応、私の期待した解答を掲載させて頂きます。
【問題3】については次の通りです。
「4個取り出し、a,b,c,dの4人に1個づつ配る」を繰り返し、余りが8個未満になった時、その個数で次のように配ります。
1個 a 2個 b、c 3個 d、a、b 4個 * 5個 * c 6個 * d、a 7個 * b、c、d*4人に1個づつ
この方法だと配った後(or配る時)に貰った個数を数える必要はありません。
【問題2】の場合は余りが3個未満になった時の個数で配ります。
◆北海道 Macyu さんからの解答。
【問題4】
これは、2人でのケーキカットの延長と考えることが出来るんじゃないかな?
2人でのケーキカットの場合moving-knife法(だっけ?)で第三者がナイフを動かし、2人のうち「ストップ」っていったほうが(ナイフが左端から右端に動く場合は)ナイフの左を取れば良い。
といった問題の延長です。
同じような方法で、やるとなると3人のうち、1人がストップっていってその後2人のうち1人が残りのカステラでストップって言えば、平等かな?って思うんですけど、実際この方法だと、最初の1人が次の2人用の分割に参加できないので最初の1人から不満がでると思われる。
A,B,Cとすると、Aがストップって言った(Aにとっての1/3以上)残りをB.Cで分ける・・Bがストップって言った。ここでAがBの取り分を見て、自分より多いと不満を感じる場合が考えられます。
ということで、この問題は、第三者のナイフより右側のカステラの1/2と思われる部分を3人がそれぞれ指し、誰かがストップと言った時点でストップと言った人が、第三者のナイフの左側をもらいます。
(ストップと言った時点でそれぞれ3人の指している部分も止まる)
そして、それぞれ3人が指しているなかで、真ん中を指していた人(例えばAさんBさんCさんといった順番に指していた場合のBさん)がその指していた部分より左側を取ります。
残りを残った人が取ります。
これで平等かつ公平です。
◆京都府 伊藤 さんからの解答。
【問題4】の答
2人で分配する場合、
aとbで分配するとすると、aとbに2等分できる線を各々ひかせます。
(ずれているとします。同じならそこで切る。)
その真ん中で親が切ります。
するとどちらも自分が主張した線より多くもらえます。
図に示すと、
・・A・B・・ |Aはaが2等分と示した線、Bはbが2等分と示した線、|は親が切った線です。
3人で分配する場合
2等分の場合と同じように3等分の線を各々にひかせます。
まず、右端について考えます。
・・・・・・・・・A・B・C・・ |Bで親がきってその右端をcがもらいます。
あと2人は2とおりあって、
・・・・A・B・・A・B・ | ・・・・B・A・・A・B・上の場合は右側をaが左側をbがもらい
◆愛知県 ひろ さんからの解答。
【問題4】
まず三人をABCとし、Aが代表して三等分する。
(Aは自分がどれを選んでも文句ないようにきる)
次にBCが選ぶ。
このときBCがそれぞれ別のを選べば問題なし。残りがAで終わり。
BCが同じ物を選んだ時、残りの二つの中からAが選ぶ。
次にBが残った二つのうちの一つを半分に切る。
Cが先に選びBは残りをとる。
そしてCがもう一つを半分に切る。
Bが先に選び残りをCに。
◆茨城県 雲隠才蔵 さんからのコメント。
【問題4】ヨッシーさんの解にコメント
「公平」の意味を「3人それぞれが『自分は少なくとも全体の1/3を取った』と考える」としてもこの切り方で は不満が出ます。
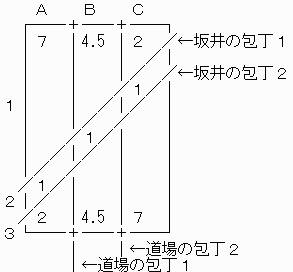
道場は他の二人から見てもきちんと三等分出来た。
坂井は本人は三等分したつもりだが、他の二人からは斜めに切ったと思われた。
このような場合、道場と陳から見た切り分け方の例として次のようになる。
(カステラ全体を30とする)

陳はA1,B2,C3を取る。7+1+7=15
坂井と道場は、1+4.5+2=7.5
ところが、陳が敢えてA1,B3,C2を取った場合、7+4.5+1=12.5
残りの分け方は、
(1) A3,B2,C1 2+1+2=5
(2) A2,B1,C3 1+4.5+7=12.5
坂井にとってはどちらでも同じに見えているが、道場にとってはどちらを取るかは重要である。
そしてどちらにせよ全体の半分は陳に取られており不満が残る。
極端な場合、坂井の包丁1と2が一致しBを対角線で切る場合、
| A | B | C | |
| 1 | 10 | 5 | 0 |
| 2 | 0 | 0 | 0 |
| 3 | 0 | 5 | 10 |
となる。
すると、陳は10+0+10=20を取ることができ、
道場は0+5+0=5しか取れない。
坂井は主観的には10/3+10/3+10/3=10。
また、反則的反例として坂井が道場に極度の悪意を抱いている場合、道場への嫌がらせで上のように切ることが可能。
自分の取り分が減ることによる不満は、道場への嫌がらせで十二分に満たされる(かもしれない)。
結果、陳と坂井は満足、道場は大いに不満足となる。
【感想】
回答でなくてごめんなさい。
eikiさんの答えがなかなか味があって面白かったです。
いろいろ考えているうちに数学からは程遠い、さらに凶悪な答えが浮かんでしまいました。
道場が「問題のナイフ」で坂井と陳を殺して独り占めしてしまう。
道場 :満足
坂井・陳:もはや不満を感じる術も無く…(合掌)
◆神奈川県 ココちゃん さんからの解答。
【問題4】
道場さんが2分の1だと思ったあたりで切る。
坂井、陳さんの両方にどちらが大きいか聞いてみる。
(1)坂井、陳さんが同じほうを選んだ場合
大きいと思ったほうのカステラを陳さんが3等分にして坂井さんに左から大きい順に並ばせる。
左から坂井さん、道場さん、陳さんの順に配る。
また先ほど選ばれなかった、坂井さんと陳さんが小さいと思ったカステラを陳さんが3等分して坂井さんに大きい順に並ばせる。
左から坂井さん、道場さん、陳さんの順に配る。
カステラは6等分されたので2切れずつです。
(2)坂井、陳さんが違うほうを選んだ場合
陳さんが大きいと思ったほうのカステラを陳さんが3等分にして坂井さんに左から大きい順に並ばせる。
左から坂井さん、道場さん、陳さんの順に配る。
坂井さんが大きいと思ったほうのカステラを坂井さんが3等分にして陳さんに左から大きい順に並ばせる。
左から陳さん、道場さん、坂井んの順に配る。
カステラは6等分されたので2切れずつです。
たぶん不平はでないとおもう。
あらかじめ「切った人には選択肢がありません」と伝えておくと、選ぶほうがなんとなく得な感じなので誰もやらないかもしれないと思いました。
切り役は適当にじゃんけんで決めるしかないような・・・。
◆富山県 萩の葉 さんからの解答。
【問題4】
なつかしい・・・
三人兄弟の一番上だったので母から与えられたお菓子を私が分けて三番目の弟から選ばせていた。
見かけは多いが実は少ない皿をひたすら作っていた。
幼い弟は他愛もないのだが真ん中の妹の目がきびしかった・・・
えげつない姉だったな〜〜
シンプルな方法としては道場さんが三等分の位置を決め、坂井さんがそれでいいかをどうか決め、陳さん酒井さん道場さんの順で取る。
但しいかにも陳さんが有利だし坂井さんは永遠にOKを出さないかもしれないので、その改良案として道場さんが三等分し、坂井さんがその内の一つを選んで三等分し、陳さん道場さん坂井さんの順で取る。
次に陳さんが残りの二つの中から選んで三等分し、道場さん坂井さん陳さんの順で取る。
残った一つを道場さんが三等分し、坂井さん陳さん道場さんの順で取る。
三人とも一番最初にカステラを取る機会が一度ずつあるのでかなり満足感はあると思う。
こうなると誰が一番有利なんだろう?
絶対に正しい三等分ができないとすると、坂井さんが一番小さいカステラを選んで三等分しようとして有利なのだろうか?となるとこの三分割を何度も繰り返してカステラをひたすら細切れにしていくか、サイコロで一番最初に三等分する人を決めるしかないのかなーーー?
◆千葉県 itochan さんからの解答。
【問題2、3】
n人での分配として、 s=k(k-1)/2 をnで割り切れるようにすればいいんですよね。
(kで割ったあまり) なし s=0 k=2 o s=1 k=3 oo s=3 k=4 ooo s=6 k=5 oooo s=10 k=6 ooooo s=15 k=7 oooooo s=21 k=8 ooooooo s=28 ……n=2のとき、k=4で s=6がnで割り切れます。
【問題3】で言うと、
n=4の表 (k=8なので、 8で割った余りに対応) 余り0 なし 1 a 2 bc 3 dab 4 cdab 5 cdabc 6 dabcda 7 bcdabcdその表にしたがって余りを割り振ります。
n=5ではk=5。
n=6の時、k=4で、全体を4で割った量を把握できればいいんですが、もう配ってしまっている時は面倒くさいですね。
(4人に配っていて既に配った量が分からない時、総数を8で割った余りがでないのも同じですが。)