◆広島県 清川 育男 さんからの解答。
【問題1】
この問題は以前にも出題されたトリボナッチ数列ですね。
階段を1段〜3段で登るとき..は?。
【問題1】
1点 1 2点 1+1,2 3点 1+1+1,1+2,2+1,3 4点 1+1+1+1,1+1+2,1+2+1, 2+1+1,2+2,1+3,3+1 5点 1+1+1+1+1,1+1+1+2, 1+1+2+1,1+2+1+1 2+1+1+1,1+2+2,2+1+2, 2+2+1,1+1+3,1+3+1, 3+1+1,2+3,3+2以上のように
答え 274通り。
【問題2】
81,147,274,504,927,1705,3136,5768
答え 5768通り。
【問題3】
T(1)=1,T(2)=2,T(3)=4
T(n)=T(n-1)+T(n-2)+T(n-3) n≧4
特性方程式は3次方程式で、「わかさひ君」さんがその解法の指針を示されましたが、実際に一般式を求められた方はおられるのでしょうか。
【コメント】
階段の問題も有名な問題ですよね。
残念ながら一般項の式は報告されていません。
求めるにはかなりの根性が必要でしょう。
◆岐阜県 水の流れ さんからの解説。
<解説>
このバスケットボ−ルも問題は、トリボナッチ数列になります。
1点=1・・・・(1通り) 2点=1+1、2・・・(2通り) 3点=1+1+1,1+2、2+1,3・・・(4通り)4点の場合は1点からの3ポイント、2点からの2ポイント、3点からの1ポイントの加算があります。
T(1)=1,T(2)=2,T(3)=4,
T(4)=T(1)+T(2)+T(3)=7
同様に、計算していくと、
{T(n)}
1,2,4,7,13,24,44,81,149,274,504,927,1705,3136、5768,・・・
したがって、
問1 T(10)= 274
問2 T(15)= 5768
問3 T(n)=T(n−1)+T(n−2)+T(n−3)
(ただし、n≧4の整数)
◆Takahisa Iida さんからの解答。
この数列の特性方程式は
χ3−χ2−χ−1=0
で、この根は実根が1つと虚根が2つです。
虚根が1より小さいので、実根をaとすると、この数列の第n項はほぼ
c×an
で表されます。ここでcは定数です。
ニュートン法でaを求めると
a=1.839286755
で、これからcを試行錯誤で求めると
c=0.618419922
となります。(これらの値は近似値です)
実際の数列と、c×anを四捨五入したものを比べると、値がほぼ一致していることが確認できます。
私の計算では、第50項までは大丈夫でした。(計算してみて下さい)
【コメント】
非常に面白いアイディアですね。
一般項を求める気がしないので、近似値を簡単に計算できるのは有用だと思います。
ただcを求めるのが大変?では。
◆広島県 清川 育男 さんからの解答。
特性方程式 χ3−χ2−χ−1=0の実根aを求めてみました。
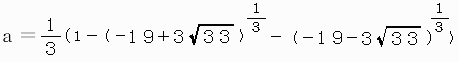
a=1.8392868
ここから、「わかさひ君」さんの指針によって隣接3項間の漸化式を求めて、さらに一般式までたどりつくのは至難の技のように思います。
◆Takahisa Iida さんからの解答。
係数cが判りましたのでお知らせします。
特性方程式の実根をaとすると、
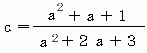
となります。
通常の連立方程式を解いてこの係数だけを求めました。
根と係数の関係も使います。
変数の置き方に少しだけ工夫しました。
他の根とその部分の係数は、面倒なので求めませんでした。