4
◆山梨県 Footmark さんからの解答。
【答え】
| 半径は | 4 | 。 |
2次元の場合、どの2点間の距離も最大値1になるのは3点までで4点以上はあり得ない。
よって、どの2点間の距離も1である3点だけを考えれば十分である。
2次元なら、辺の長さ1の正三角形に外接する円の半径なので
3 | 。 |
3次元の場合、どの2点間の距離も最大値1になるのは4点までで5点以上はあり得ない。
よって、どの2点間の距離も1である4点だけを考えれば十分である。
3次元なら、辺の長さ1の正四面体に外接する球の半径なので
4 | 。 |
◆愛知県 juin さんからのコメント。
Footmarkさんの解答について
2次元の場合
| 点が3つの場合、半径 | 3 | の円に入ると思います。 |
| しかし、4つ目の点がその円の中心から | 3 | 以内にあることが理解できません。 |
3次元の場合
| 点が4つの場合、半径 | 4 | の球に入ると思います。 |
| しかし、5つ目の点がその球の中心から | 4 | 以内にあることが理解できません。 |
◆山梨県 Footmark さんからのコメント。
2次元でも3次元でも同じですが、わかり易い2次元から説明します。
2点しかないのなら、明らかに2点の中点を中心にした半径1/2の円内にすべての点が含まれます。
ところが、辺の長さ1の正三角形の頂点に3点があると、どの2点の距離も1以下なのに半径1/2の円ではすべての点は収まりません。
3点の場合は、このようにどの2点の距離も最大値1になるときが円も最大となり、
| 解答で示したように円の半径は | 3 | は必要です。 |
では、4点以上の場合はどうでしょう。
| 3点での最大円(半径 | 3 | )がさらに大きくなるでしょうか? |
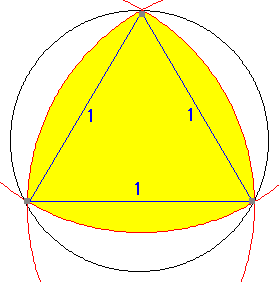
何故なら、4点目以降の残りのすべての点は、図のように元の3点によるルーローの三角形の内部(黄色部分)になければなりません。
(ルーローの三角形の外部にも点が存在すると、元の3点の中の少なくとも1点とは距離が1を超えてしまいます。)
| ですから、それより大きい正三角形の外接円(半径 | 3 | )の外では |
| 結局、すべての点は半径 | 3 | の円内にあることになります。 |
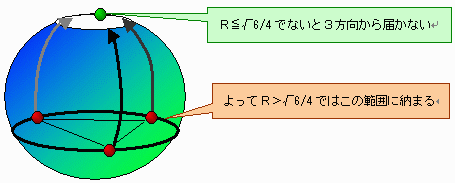
| 3次元なら、4点での最大球は半径 | 4 | であることは容易に理解できます。 |
| 5点以上なら、4点での最大球(半径 | 4 | )がさらに大きくなるでしょうか? |
二次元がルーローの三角形なので、三次元ではさしずめルーローの四面体と表現することにします。
これは、正四面体の各頂点を中心に他の3頂点をすべて含む4つの球面でできた四面体です。
5点目以降の残りのすべての点は、元の4点によるルーローの四面体の内部になければなりません。
(ルーローの四面体の外部にも点が存在すると、元の4点の中の少なくとも1点とは距離が1を超えてしまいます。)
| ですから、それより大きい正四面体の外接球(半径 | 4 | )の外では |
| 結局、すべての点は半径 | 4 | の球内にあることになります。 |
2次元の場合、どの2点間の距離も最大値1になるのは3点までで4点以上はあり得ない。
よって、どの2点間の距離も1である3点だけを考えれば十分である。
3次元の場合、どの2点間の距離も最大値1になるのは4点までで5点以上はあり得ない。
よって、どの2点間の距離も1である4点だけを考えれば十分である。
解答の中で、上のように表現した理由はここにあります。
◆愛知県 juin さんからのコメント。
Footmarkさんの解答について
2次元の場合
平面上の3点が1辺の長さ1の正三角形をつくっていれば、残の点もルーローの三角形内にあることはわかります。
問題はそうなっていないとき、
| 半径 | 3 | の円に点がおさまるかということです。 |
4点A,B,C,Dがある場合を考えます。
A,Bの距離を1とし、Cがルーローの三角形の曲線上にあり、しかも頂点にない場合を考えます。
このとき4つめの点は、ABを1辺とする正三角形に外接するルーローの三角形の外にあってもよいのです。
| この場合にも半径 | 3 | の円におさまるかというのが疑問です。 |
◆大阪府 macsyma2e さんからの解答&コメント。
もとの集合をXとし、
X⊂R2 and |X|≧3 の場合の十分性を述べます.
まず、異なる任意の3点A,B,C∈Xに対して、
| A,B,Cの全てを含む半径の長さ= | 1 | の閉円板(以下、円) |
| △ABC(退化してもよい)の最大角の大きさが | π 2 | 以上π以下の場合、 |
| その対辺を直径とする円は3点を含み、半径の長さ≦ | 1 2 | . |
△ABCが鋭角三角形の場合、
外心をPとおくと、Pは△ABCの内部なので、
| たとえば∠APB≧ | 2π 3 | 、つまり∠PAB≦ | π 6 | としてよく、 |
| AP× | 2 |
≦ | AB 2 | ≦ | 1 2 | .□ |
上のことは、 Xの各点を中心とする
| 半径の長さ= | 1 | の円をA(1),...,A(n)とおくと、 |
と換言出来ます.
ところが、凸解析でよく知られた定理(Helly)から
3個以上の空でない凸集合 A(1),...,A(n) について、
任意のi,j,kに対し、A(i)∩A(j)∩A(k)≠空集合
ならば、A(1)∩...∩A(n)≠空集合
なので、上記のA(1)∩...∩A(n)の任意の点を中心とする
| 半径の長さ= | 1 | の円は、Xを含んでいます. |
【ひとこと】
Hellyの定理の証明は、凸一次結合の性質と集合の個数についての帰納法から得られます.
> Footmarkさん
十分性の考察において、正三角形が利用出来るのは何故でしょう.
任意の3点からの帰着方法をご案内頂けますか?
◆山梨県 Footmark さんからのコメント。
私にとっては当たり前に思えるので、なかなかうまく説明ができず申し訳ありません。
3点でまず三角形を形成させてから4点目以降を考察した説明が、かえって解り難くしたかもしれません。
2次元で説明します。
まず、すべての2点間の距離のなかで最大のものを採ります。
仮にその距離をRとします。
そこで、半径Rの3つの弧でできるルーローの三角形を作成します。
すると選ばれた2点は3頂点の内の2頂点にある筈です。
さらに、残りすべての点も同一平面上に書き入れるものとします。
すると、距離や方向がどうであっても、すべての点はルーローの三角形の内部にある筈です。
何故なら、そうでなければ最大の距離を採った前提に矛盾するからです。
| このとき、このルーローの三角形の外接円の半径は | R | です。 |
| 0<R≦1 ですから、最大の時の外接円の半径は | 1 | です。 |
同様に、本問である3次元でのすべての点は半径1の4つの球面によるルーローの四面体の内部にあります。
よって、求める球の半径は
| この四面体の外接球の半径ですから | 4 | になります。 |
>macsyma2e さんへ
数学専門家ではないので「Hellyの定理」とか「凸一次結合」とかいった言葉はまったく初耳でした。
私の場合、粗末であってもその都度自分なりに発見した解法を用いるのが常です。
そのため問題に対する常套的手法でない場合も多々あります。
でも、とりあいず二次元の答えは正解のようなので、ひとまず安心しました。
◆愛知県 Y.M.Ojisan さんからのコメント。
Footmarkさんの証明について、
2次元の場合、最終解答に対する反例ではありませんが、
対角線の長さが1である正方形ないし正5角形の頂点が
| 半径は | 1 | の円内であると言えるのでしょうか。 |
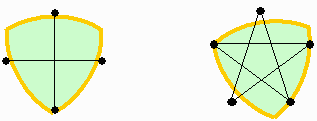
◆愛知県 Y.M.Ojisan さんからの解答。
【2次元の場合の初等的解答】
背理法によります。
ある平面上の点群があって、
| これを包む最小の円の半径RがR> | 1 | であるとします。 |
このとき少なくともこの円上に3点があると言えます。
∵円上の点が1点以下の場合、明らかにもっと小さな円で包む事ができます。
円上の点が2点の場合それは、直径を示す点でなければなりません。
| 従って半径は | 1 2 | でなければならず仮定と矛盾します。 |
よって、円上の点の数は3以上です。
| 以上より、半径R> | 1 | 上に3点以上の点があって、 |
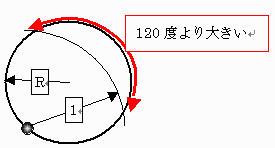
| まず一点を考えると、R> | 1 | で点間距離1以下の条件より |
つまり第2の点は第1の点の両側120度未満の位置にのみ存在可能です。
従って、この弦上で1以下の距離を考えるときは円周にそって120度以下の距離を考えれば良く、一次元での点の分布範囲の問題に還元できます。
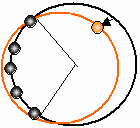
結局、点群は円上の120度以下の弦上にのみ存在していなければなりません。
これはもっと小さな円で全体を包める(下図)ということですから、仮定と矛盾します。
| よって、Rは | 1 | 以下です。 |
【3次元の場合】
2次元同様 表面に直径が2次元問題相当で120度以上の穴があいた球殻上の4個以上の点の分布の問題に還元され、実は半球より小さい、直径が2次元問題相当で120度以内の範囲に分布していなければならず、Rはもっと小さくできるという矛盾に導けると推定されます。
◆山梨県 Footmark さんからのコメント。
【Y.M.Ojisan さんの質問に対して】
>対角線の長さが1である正方形ないし正五角形の頂点が半径は1/√3 の円内であると言えるのでしょうか。
| 結論から述べると、この時の半径は | 1 | 未満ですから、 |
| 当然半径 | 1 | の円内にあると言えます。 |
1が許される2点間の距離の最大値ですから、正n角形では最長の対角線の長さが1ということになります。
また、どんな正n角形も円に外接しますから、
nが偶数なら最長の対角線は外接円の直径となり
| 半径は | 1 2 | です。 |
nが奇数ならnが大きくなるほど最長の対角線は外接円の直径に近づき
| 半径は | 1 2 | に近づきます。 |
最長の対角線を外接円の弦と考えると、同じ長さの弦が外接円の中心から遠いほど外接円は大きい筈です。
ですから、正多角形において最長の対角線が1である場合では正五角形の外接円が最大です。
ところが、正五角形の最長の対角線よりも辺長1の正三角形の各辺の方が外接円の中心から離れています。
それ故、最長の対角線が1であるような正多角形では
| 外接円の半径は | 1 | 未満です。 |
ところで、3点が正三角形の頂点ならすべての点を含む円の半径は
| 1 | は必要であることは既に示しました。 |
| ですから、半径が | 1 | より小さい場合では反例とはなりません。 |
添え図より判断するに、
>対角線の長さが1である正方形ないし正五角形の頂点が、半径1の3つの弧でできたルーローの三角形内にあると言えるでしょうか。
の誤述であると仮定します。
| 最大円(半径 | 1 | )が必要となる時はルーローの三角形内にあると言えますが、 |
どのような3点であろうと、その3点が辺長1の正三角形を形成するなら、
| 半径 | 1 | の最大円が必要になります。 |
その時その3点は円周上にあり、それ以外の点はその3点を頂点とするルーローの三角形の内部(周上も含む)にあります。
(このルーローの三角形の内部にあるどのような2点も距離は1以下です。)
(以下は証明ではありません。)
先のコメントでも示したように2点しかない場合は
| 全ての点を含む円の半径 | 1 2 | で十分です。 |
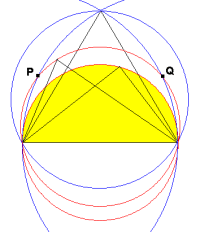
そこで、長さ1の弦と、その弦の両端からの距離がいずれも1以下である1点とでできる三角形を考えてみます。
三角形の外接円の中心が三角形の外部にある時は、この三角形は弦が直径となる半円の内部にあります。
| ですから、全ての点を含む最小円の半径は | 1 2 | です。 |
三角形の外接円の中心が三角形の内部にある時は、外接円の半径Rは明らかに、
| 1 2 | <R≦ | 1 |
です。 |
先の結果とこれらのことより、点の数が複数なら、
| 全ての点を含む円の半径は | 1 2 | 以上 | 1 |
以下です。 |
ですから、点の数や位置により異なりますが、どのようなものであっても
| 半径 | 1 | の円なら全ての点を含みます。 |
| また、半径 | 1 | 未満の円なら同じ条件を満たせず不十分です。 |
【Y.M.Ojisan さんの証明について】
Y.M.Ojisanさんの証明の論法を要約すると以下です。
| ● R> | 1 | の円なら、どのような円も縮小できる。 |
| ● 縮小された円ならR> | 1 | と矛盾する。 |
| ● 縮小された円がR> | 1 | でないなら、R≦ | 1 | である。 |
問題は上の2番目です。
Y.M.Ojisanさんの文章では
>これはもっと小さな円で全体を包めるということですから、仮定と矛盾します。
どうして仮定と矛盾すると言えるのでしょうか?
| 元々、R> | 1 | の仮定しかないので、その円が縮小できたからと言って |
| 「R> | 1 | ではない」とは言えないと思います。 |
| ですから、R≦ | 1 | であるとは結論できません。 |
◆愛知県 Y.M.Ojisan さんからのコメント。
Footmarkさんの御指摘の2点はいずれも同じ論点ですのでまとめて回答致します。
Rの持つ重要な性質は最小値であるということです。
極論例を踏襲すれば、「R=100は最小値」であると言っておきながらR=99が存在すれば100は最
小値でなかったわけです。
よって、1より大きいRは最小値にはなりえないわけですから、Rは少なくとも1以下といえます。
◆山梨県 Footmark さんからのコメント。
【Y.M.Ojisan さんの証明について】
述べたいことが旨く伝わっていないようなので、以下に詳しく説明します。
| ● R> | 1 | の円なら、どのような円も縮小できる。 |
| ● 縮小された円ならR> | 1 | と矛盾する。 |
| ● 縮小された円がR> | 1 | でないなら、R≦ | 1 | である。 |
| 仮に上の1番目が真ならRは限りなく | 1 | に近づくか、 |
| あるいは | 1 | 以下になるかのどちらかです。 |
| 何故なら縮小された円が仮にR> | 1 | であるなら、 |
| 再帰的に1番目に戻ってさらに縮小できるからです。 |
仮に1番目が真としても2番目が成立するとは限らないことは、以下の反例で理解できると思います。
| 現半径と | 1 | との平均の半径に円を縮小させても、 |
| ● R> | 1 | の円なら、どのような円も縮小できる。 |
| ● 縮小された円ならR> | 1 | と矛盾する。 |
分りやすい反例なら、
◆愛知県 Y.M.Ojisan さんからのコメント。
下記(1)の説明不足であるという御指摘の趣旨ならYesです。
(1) 証明の冒頭にあるように、Rは少なくとも3点を通過しています。
従って、点の数をnとするとその種類は高々nC3です。
| よって御指摘の限りなく | 1 | 以上に近づくケースは排除できます。 |
◆茨城県 えいじ さんからのコメント。
山梨県 Footmark さんからの2回目の回答に対するコメント。
(問題から離れますが、新たな問題の発生)
Footmarkさんは、ルーローの三角形の、三次元への拡張の「ルーローの四面体」に言及していますが、そのルーローの四面体を実際に製作して、インターネット上で発表した人が、2名います。
・岩手の高校の数学教師のみやじさんの<取れたて通信>の中
『http://www25.tok2.com/home/toretate/d020103.html』
・YPC横浜物理サークルの車田浩道さん
『http://www.geocities.co.jp/Technopolis-Mars/8494/NEWS/ypc145/ypc145.htm#ルーローの四面体』
ところが、このルーローの四面体が「定幅でない」事が、同じ方々から発表!
『http://www25.tok2.com/home/toretate/d020104.html』
『http://www2.hamajima.co.jp/~tenjin/ypc/ypc021.htm』
約2.5%膨れていることが判ったのです。
ゆえに、ルーローの四面体の内部の点同士でも、距離1より大なる、点の組があることになります。
(但し、これはFootmarkさんの回答への反例にはなりません)
ここで問題です。
ルーローの四面体を「定幅に」改良できないでしょうか?
不可能でしょうか?
私は、答えを知りません。
上記の2名も解答を得ていないようです。
◆山梨県 Footmark さんからのコメント。
えいじさんのコメントに対するコメントです。
「ルーローの四面体は定幅でない」
最初は、そんな馬鹿なと思いつつ紹介されたURLをすべて覗いてみました。
なるほど、そのようですね。
興奮と感動を覚えずにはいられませんでした。
えいじさん、ありがとうございます。
すると、定幅四面体って一体どんな形になるんでしょうね。
とても興味があります。
◆愛知県 Y.M.Ojisan さんからのコメント。
定巾の立体として球でなければよいだけなら、ルーローの三角形の回転体があります。
栗みたいな形。
さらに定巾の左右対称図形はルーロー三角形を単に太らせただけ以外にも無限にありますから、何かできるかも。