

2
◆石川県の高校生 アビュー さんからの解答。
問題が解けたのかちょっと自信がないのですが、こんな感じでどうでしょうか?
【問題1】
a + b√2 = 0 ⇒ a = b = 0を証明せよ。
(a,b:有理数)
式を変形すると
| b = - | a | = - | a 2 |
ここで、aが0でない有理数とする。
すると、bには必ず を無理数の倍数として含むことになる。
を無理数の倍数として含むことになる。
これは問題の定義(a,b:有理数)に反するから、a = 0である必要がある。
このことから、これを問題式に代入すると、
b = 0よりb = 0。
= 0よりb = 0。
∴a = b = 0
【問題2】
a + b + c
+ c = 0 ⇒ a = b = c = 0を証明せよ。
= 0 ⇒ a = b = c = 0を証明せよ。
(a,b,c:有理数)
(1)の手順と変わらない。
a,bのうち少なくとも1つが0でない何らかの有理数のとき、
a + b + c
+ c = 0が成り立つかを考える。
= 0が成り立つかを考える。
a + b + c
+ c = 0、式変形して
= 0、式変形して
| c = | -(a + b ) ) |
= | - (a + b (a + b ) )3 |
 が残る。
が残る。 = 0よりc = 0。
= 0よりc = 0。【問題3】
a + b + c
+ c + d
+ d = 0 ⇒ a = b = c = d = 0を証明せよ。
= 0 ⇒ a = b = c = d = 0を証明せよ。
(a,b,c,d:有理数)
(2)と同様に考える。
a,b,cのうち少なくとも1つが0でない何らかの有理数のとき、
a + b + c
+ c + d
+ d = 0が成り立つか考える。
= 0が成り立つか考える。
a + b + c
+ c + d
+ d = 0、
= 0、
式変形して
| d = | -(a + b + c + c ) ) |
= | - (a + b (a + b + c + c ) )5 |
 は残る。
は残る。 = 0よりd = 0。
= 0よりd = 0。【問題4】
n≧1,a0,a1,a2,...,anが有理数、
P1,P2,...,Pnは相異なる素数とするとき、
a0 + a1√P1 + a2√P2 + ... + an√Pn ⇒ aj = 0
(j = 0,1,2,...,n)であることを証明せよ。
a0,a1,a2,...,an-1のうち少なくとも1つが0でない何らかの有理数のとき、
a0 + a1√P1 + a2√P2 + ... + an√Pnが成り立つか考える。
式変形をして、
| an = | -(a0 + a1√P1 + a2√P2 + ... + an-1√Pn-1) √Pn |
| an = | -√Pn(a0 + a1√P1 + a2√P2 + ... + an-1√Pn-1) Pn |
◆出題者のコメント。
アビューさん、まずはこの問題に挑戦してくれてありがとうございます!
早速ではありますが、アビューさんの解答についてコメントさせてもらいます。
この問題を要約すれば
『異なる整数達(本問では素数達としました)の平方根達をそれぞれ有理数倍(すべて0倍は除く)してから足して、その結果別の整数の平方根を作れるか?
⇒作れない!』 を示すことです。
これは当たり前なことではありません!
どういうことかというと、例えばP,Q,Rを異なる素数とするとき
(有理数)=2√P+3√Q+4√R ・・・★
という式を考えてみましょう。
★は嘘なのですが、嘘だ!ということが当たり前ではない!ということです。
しつこく言うと、式の中に√が残っているからといって、それが無理数だと断定は出来ません。
もしかしたら √2-√3+√5-√7+√11-√13+√15-√17+√19=0かもしれない・・・。
(もし無理数と断定する場合には、★の右辺を有理数Aと仮定して矛盾をだす必要があります。
Aが無理数であることを示すには、Aが有理数であると仮定して
| (A= | p q |
,p,qは整数)、矛盾を示すことによってのみ、示されます。) |
本問はこの見かけ上「当たり前なこと」を、ちゃんと示すことが要求されています。
だから、式を変形した結果、★のような式が出来たからといって、「おかしい、これは矛盾だ」としては答えにはなりません。
・・・と、いろいろ説明してきましたが・・・日本語がずらりずらりと続いてわかりづらかったかもしれません(ごめんなさい)。
アビューさんからもらった解答に実際あたってみてみます。
(問題1に関して)
アビューさんは式変形の結果、
| (有理数b)=(有理数- | a 2 |
)×(無理数 )という式を得ましたね。 )という式を得ましたね。 |
 を無理数の倍数として含むことになる。」としています。
を無理数の倍数として含むことになる。」としています。 の有理数倍になる」ということですね。
の有理数倍になる」ということですね。
次に「これは問題の定義(a,b:有理数)に反する」とありますが、おそらくこの議論は、有理数の 倍が有理数になるわけがない!ということを、暗黙のうちに認めてはいないでしょうか?
倍が有理数になるわけがない!ということを、暗黙のうちに認めてはいないでしょうか?
もしそうならこれは正しい証明とはいえません。
これは、上の方でもいったように、これこそ示して欲しいことなのです!
「 の有理数倍(0倍ではない)のもの」が無理数であること を暗黙のうちに認めてしまっているのです!
の有理数倍(0倍ではない)のもの」が無理数であること を暗黙のうちに認めてしまっているのです!
・・・どうでしょうか?
( くどくどごめんなさい。ちなみに が無理数であることは当たり前としていいです。証明は教科書に載ってます。)
が無理数であることは当たり前としていいです。証明は教科書に載ってます。)
◆神奈川県 テトラン さんからのコメント。
>このとき、aの第n項を除く数列の値が0でないときは全ての根号が外れない。
>(Pの数列に同一の素数は存在しないから)
そうとは限りません。
同一の素数が存在しなくとも、
a1√P1+a2√P2+…+an-1√Pn-1=k√Pnを満たす
有理数a1〜an-1及びk (k≠0)が存在していれば根号は外れます。
従って、根号が外れないことを証明するには、この式が成り立つa1〜an-1及びkが
a1=a2=…=an-1=k=0に限られることを証明しなければなりません。
そして、この式は
a1√P1+a2√P2+…+an-1√Pn-1+(−k)√Pn=0
と変形できるので、これで振り出しに戻ってしまいます。
>またaの第n項を除く数列の値のうち少なくとも1つが0でないときも、Pの数列には同一の素数は存在しないから、根号は外れない。
同じ理由により、根号が外れないとは限りません。
◆高知県 blue さんからの解答。
【問題1】
a+b =0のとき、b≠0とする。
=0のとき、b≠0とする。
このとき、 =− =− |
a b |
となり |
【問題2】
a+b +c
+c =0のとき、c≠0とする。
=0のとき、c≠0とする。
a+c =−b
=−b
両辺を2乗すると
a2+3c2+2ac =2b2
=2b2
2ac =2b2−a2−3c2
=2b2−a2−3c2
a≠0とすると
 = = |
1 2ac |
(2b2−a2−3c2) |
 +c
+c =0
=0 =− =− |
b c |
 =− =− |
2b c |
 =0
=0【問題3】
a+b +c
+c +d
+d =0のとき、d≠0とする。
=0のとき、d≠0とする。
a+d =−(b
=−(b +c
+c )
)
両辺を2乗すると
a2+2ad +5d2=2b2+2bc
+5d2=2b2+2bc +3c2
+3c2
a2+5d2−2b2−3c2+2ad −2bc
−2bc =0
=0
[問題2]よりa2+5d2−2b2−3c2=0,ad=0,bc=0
後者2つよりa=0,b=0,c=0,d=0
a=0のとき
b +c
+c +d
+d =0
=0
b +d
+d =−c√3
=−c√3
両辺を2乗すると
2b2+5d2+2bd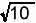 =3c2
=3c2
2bd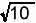 =3c2−2b2−5d2
=3c2−2b2−5d2
b≠0とすると
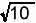 = = |
1 2bd |
(3c2−2b2−5d2) |
よってb=0でありc +d
+d =0
=0
 =− =− |
c d |
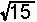 =− =− |
3c d |
 +d
+d =0
=0 +c
+c =0
=0【問題4】
(i)n=1のとき
a0+a1√P1=0⇒aj=0(j=0,1)
(∵[問題1]より)
(ii)n=k(≧1)のとき
a0+a1√P1+a2√P2+…+ak√Pk=0⇒aj=0(j=0,1,2,…,k)と仮定する。
a0+a1√P1+a2√P2+…+ak+1√Pk+1=0のときak+1≠0とする。
| √Pk+1=− | 1 ak+1 |
(a0+a1√P1+a2√P2+…+ak√Pk) |
◆出題者のコメント。
blueさん解答ありがとうございます。
この数学の部屋に来るようになって初めての出題がこれですが、いろんな方に考えてもらえるのはとても嬉しいです。
毎日楽しみに解答を待っています。
では出題者としてコメントをさせて頂きます。
問題1から問題3に関して。
平方による式変形で√の数を減らしていき、結局問題1の形に帰着させる。正しい解答だと思います!
問題4に関して。
疑問点が一つあります。
>よって、a0+a1√P1+a2√P2+…+ak√Pk≠0
>このとき、∀aj=0(j=0,1,2,…,k)は明らかに不適なので、
>∃aj≠0(j=0,1,2,…,k)
>これは仮定の裏であり成り立たない。(矛盾)
最後のところですが、つまり、「仮定の裏が成り立たないはずなのに、成り立ってしまうからこれは矛盾。」
ということでしょうか。
仮定の裏、の対偶は何になるでしょうか?
それは仮定の逆です。
いま、仮定の逆は明らかに成り立ちます。
従って仮定の裏は正しいことです。
だから矛盾ではありません。
どうでしょうか?
また、この証明では、√の中身が0でない数なら何でもOKとなってしまいます。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題4】
感想に「√の中身を素数としましたが、もっと一般化されます」とありますが、一般化したほうが証明しやすいので、
Piは因数分解すると素因数の冪が総て1である数とします。
このより広い範囲でも問題4の定理が成立すれば、その一部である問題4でも成立することが証明されたことになります。
<記号>
(1) 形式上 P0=1とします。
(2) a0√P0+a1√P1+a2√P2+…+an√Pm−1
で表される数の集合をQmとします。
(3) また特定の Piの組による集合を Qm(P)⊂Qm とします。
(4) P0〜Pm−1が 素数π1〜πnによる総ての組合せを網羅しているとき、
即ちm=2n の場合のQmを特にQ2^n とします。
つまりたとえば Q2^2は
{f|f=a0+a1√2+a2√3+a3√6} や
{g|g=a0+a1√5+a2√3+a3√15} 。。。なる集合の集合です。
また前者は
Q2^2({1,2,3,6}) ないし
Q2^2({1,2}×{1,3}) です。
【補題】
拡大問題4が成立するなら Q2^n(P)は 通常の4則に対して体である。
∵ 加算、減算、乗算が成立することは 明らかである。
除算に関してのみ解説する。
所謂 「分母の有理化」 を行えば形としてQ2^n(P)の要素に出来ることは明らかである。
拡大問題4が成立しているという前提にたてば Q2^n(P)の要素fが0になるのは ai総てが0のときのみであり、
有理化の過程で分子分母に0をかける事はない。よって体である。
【証明】
n=1のとき a0+a1√P1=0 は
a02=a02P1 と変形され、これが0でないとすると、P1に含まれる素因数の冪の偶奇性が一致せず、ありえない。
よって a0=a1=0 である。
以下 n=k−1 (1≦k≦2 は確認済み) で成立しているとして、
K>2の場合を数学的帰納法で証明する。
a0√P0+a1√P1+a2√P2+…+an√Pm−1=0 -----(A)
が n=kで成立する場合が在ったとする。
一般性を失わず P1 (a1≠0) の素因数の一つ π1 に着目する。
(A)式は
f√π1=g f,g∈Q2^k−1(P/{1,π1})
と書ける。
f=0 であれば g=0 であり、 n=k−1で拡大問題4が成立しているので ai総て0である。
即ち n=kで成立する。
f≠0 であれば <補題より>
√π1=h=g/f h∈Q2^k−1(P/{1,π1}) -----(B)
と表される。さらに同様に n≧2なので
さらに π2≠π1があって、
√π1=h=x+y√π2 x,y∈Q2^k−2(P/{1,π1,π2,π1*π2}) -----(C)
とすることができ、これを 両辺2乗すると
x2+π2y2−π1+2xy√π2=0 -----(D)
である。 (D)式左辺は全体として Q2^k−1(P/{1,π1}) の要素であり
x2+π2y2−π1 、2xy のそれぞれは、
Q2^k−2(P/{1,π1,π2,π1π2}) の要素である。
つまり x2+π2y2−π1にはπ2を因数にもつPiはなく、
一方、2xy√π2のPiは必ずπ2を因数にもっている。
よって、それぞれ0でなければならず
x2+π2y2−π1=0 、2xy=0 である。
2xy=0 より x=0 か y=0である。
x=0のとき (D)は
√(π1/π2)=y -----(E)
y=0のとき (B)は
√(π1)=x -----(F)
であり、(B)と同じ 有理数の平方根=h の形式である。
ただし、x,y∈Q2^k−2(P/{1,π1,π2,π1*π2})でkが一つ下がっている。
(E)式では √π1 の部分が√(π1/π2)となっているが xy=0を導出する際、
有理数としての特性のみ使用しているので同じ結論が得られる。
以上を繰り返すことにより、xまたはy∈Q2^0まで下げることが出来き、このとき x、yは有理数なので矛盾である。
よってx=y=0であり、h=0であり g=0である。
即ち f=0であり これは f≠0 の仮定に反する。
以上より aiは総て0である。
【補足】
分かりににくいのでn=3 π={2,3,5} m=8 で解説する。
まずn=0、1、2 の 場合が成立しているとは
<n=0>
a0=0 ならば a0=0
<n=1>
a0+a1√2=0 |a0+a1√3=0|a0+a1√5=0 ならば a0=a1=0
<n=2>
a0+a1√2+a2√3+a3√6=0 |a0+a1√2+a2√5+a3√10=0|
a0+a1√3+a2√5+a3√15=0 ならば
a0=a1=a2=a3=0
以上が成立している状態である。
証明すべきことは
a0+a1√2+a2√3+a3√6+a4√5+a5√10+a6√15+a7√30=0 ならば
a0=a1=a2=a3=a4=a5=a6=a7=0
であり、これが成立すれば
a0+a1√2+a2√3+a4√5=0 ならば
a0=a1=a2=a4=0 と言えること。
π1=2 に着目して変形すると
(a0+a2√3+a4√5+a6√15)+√2(a1+a3√3+a5√5+a7√15)=0
より
√2=b0+b1√3+b2√5+b3√15
さらに π2=5 に着目して変形すると
√2=(b0+b1√3)+√5(b2+b3√3)
である。両辺2乗すると
2 = (b0+b1√3)2+5(b2+b3√3)2+2√5(b0+b1√3)(b2+b3√3) −−(*)
(b02+3b12+5b22+15b32−2)+(2b0b1+2b2b3)√3+(2b0b2+6b1b3)√5+(2b0b3+2b1b2)√15
<n=2>での成立状態から 各係数は0である。
つまり (2b0b2+6b1b3)=0 (2b0b3+2b1b2)=0であって
すなわち (b0+b1√3)(b2+b3√3)=0である。
(b0+b1√3)=0の場合 (*)は 2=5(b2+b3√3)2
(b2+b3√3)=0の場合 (*)は 2=(b0+b1√3)2
前者の場合 計算すると
0=(5b22+15b32−2)+(10b2b3)√3
<n=1>での成立状態から 各係数は0である。
つまり b2b3=0であって
すなわち b2=0 または b3=0である。
b2=0 の場合 15b32=2
b3=0 の場合 5b22=2
であって成立しない。
◆出題者のコメント。
Y.M.Ojisanさん、丁寧な解答ありがとうございます。
正解だと思います!
体のところの議論を除けば高校生でも理解ができる解答ですね。
まだまだいろいろな方の解答を待ちたいので、また改めてコメントさせてください。
◆出題者の再コメント。
出題後に気づいたんですが、『5個の有理数』でも同じ問題がありました。
Y.M.Ojisanと本質的には同じと思われる解法が、古いですが、数学セミナーのNOTE欄(76年4月号、84年
5月号)にも載っています。
是非、参照してみてください。
僕自身は、まったく初等的ではありませんが、
事実:「n次の代数体にはn個の共役写像がある」を使うもので
した。
問題1であれば、Q( )が定義域で、
)が定義域で、
Qでは動かず を−
を− に写す写像は同型で、
に写す写像は同型で、
0=a+b の両辺にこの写像を作用させれば
の両辺にこの写像を作用させれば
0=a−b√2を得ます。
これからa=b=0を得る・・・のような感じです。
問題2〜4も同様(+α)です。
自分の方法で一般のn乗根に向けて拡張を試みましたが、
n≧5ではうまくいきませんでした。
また、Y.M.Ojisanさんの解法を真似てみましたが、僕では上手くいきませんでした。
成り立ちそうだけど、どうなんでしょうか。