◆山梨県 Footmark さんからの解答。
【答え】
2
【証明】
編み目に沿って進むときは、最短経路をとるものとする。
(そうでないと、L(P,Q)/d(P,Q) はいくらでも大きくできる。)
〔P,Qが同一格子線上にあるとき〕
L(P,Q)/d(P,Q) は常に1。
〔P,Qが同一格子線上にないとき〕
(1) P,Qの、一方が縦の格子線上にあり、もう一方が横の格子線上にあるとき
途中1回直角に曲がるだけで、PからQに進むことができる。
(2) P,Qの両方とも縦(横)の格子線上になく、かつ、P,Qの間に縦(横)の格子線があるとき

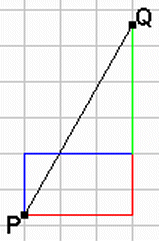
図の青と緑の経路のように、PからQに進むには少なくとも2回は直角に曲がらなければならない。
ところが、図の青い経路は赤い経路と長さが等しいので、結局(1)のときと一緒である。
すると、L(P,Q)/d(P,Q) は、直角三角形の [直角を挟む2辺の長さの和/斜辺の長さ] である。
ところで、直角三角形に外接円を描くと、斜辺は直径にあり、直角である頂点は円周上にくる。
そこで、XYを斜辺とする直角二等辺三角形XYZで考えると、
2点X,Yからの距離の和がXZ+YZとなる点は、Z点を除いてすべて外接円の外側の楕円上になる。
よって、[直角を挟む2辺の長さの和/斜辺の長さ] が最大となるのは、直角二等辺三角形のときである。
すると、(1)と(2)におけるL(P,Q)/d(P,Q)の最大値は 。
。
(3) P,Qの両方とも縦(横)の格子線上になく、かつ、P,Qの間にも縦(横)の格子線がないとき
L(P,Q)/d(P,Q)を最大にするには、L(P,Q)をできるだけ大きく、d(P,Q)をできるだけ小さくすればよい。
L(P,Q)の可能性として、左(下)側経路と右(上)側経路が考えられるが、
[左(下)側経路の長さ]+[右(上)側経路の長さ]=2×|Pのy(x)値ーQのy(x)値|+2 。
ところで、L(P,Q)は最短経路なので、L(P,Q)の最大は左(下)側経路と右(上)側経路の短い方の最大距離。
よって、L(P,Q)の最大値=|Pのy(x)値ーQのy(x)値|+1 。
また、明らかに、d(P,Q)の最小値=|Pのy(x)値ーQのy(x)値| 。
すると、L(P,Q)/d(P,Q)={|Pのy(x)値ーQのy(x)値|+1}/|Pのy(x)値ーQのy(x)値|
ここで、L(P,Q)/d(P,Q)を最大にするには、|Pのy(x)値ーQのy(x)値|を最小にすればよい。
P,Qの両方とも縦(横)の格子線上にないので、どちらも横(縦)の格子線上にある筈。
しかも、P,Qは同一格子線上にないので、|Pのy(x)値ーQのy(x)値|は1以上の整数である。
それ故、|Pのy(x)値ーQのy(x)値|の最小値は1。
よって、(3)のときのL(P,Q)/d(P,Q)の最大値は2。
 <2なので、〔P,Qが同一格子線上にないとき〕は、L(P,Q)/d(P,Q) の最大値は2。
<2なので、〔P,Qが同一格子線上にないとき〕は、L(P,Q)/d(P,Q) の最大値は2。
〔P,Qが同一格子線上にあるとき〕が常に1で、〔P,Qが同一格子線上にないとき〕の最大値が2なので、
L(P,Q)/d(P,Q) の最大値は2。
証明終わり。