
◆広島県 清川 育男 さんからの解答。
【問題1-1】
1,2,3,4 を隣りあった2つの数字を置換して
4,3,2,1にするのに要する回数だけ本数が必要である。
3+2+1=6
答え 6本。
【問題1-2】
まず1と4を置換するのに必要な本数は、
(2+1+2=5)5本。
残りの1本を2と3の間にいれることになる。
すでに入れている5本に影響をあたえず入れることの出来る個所は2つ。
したがって、2通り出来る。
答え 2通り。
【問題2-1】
4+3+2+1=10
答え 10本。
【問題2-2】
まず1と5を置換するのに必要な本数は、
(2+2+1+2=7 2+1+2+2=7)
7本。
残りの3本を2と3の間または3と4の間に7本に影響しないように入れる。
(1×2+1×2)×2=8
イ)2本 4本 4本 2本
ロ)2本 3本 3本 2本
2通りのパターンがある。
答え 8通り。
【問題3】
必要な本数は、
|
((n-1)+1)(n-1) 2 |
| = |
n(n-1) 2 |
| 答え |
n(n-1) 2 | 本。 |
何通りかは再チャレンジします。
図が書けないのが残念です。
【コメント】
本数については全て正解だと思います。
あみだくじの個数は???
本数はnC2本として(なぜでしょう)、あとはあみだくじが何通りあるかが問題ですね。
◆広島県 清川 育男 さんからの解答。
【問題1-2】
n=4の場合、
間違っていました。
( , , )は左からの横線の数
(1,2,3) 1通り
(1,3,2) 2通り
(2,2,2) 2通り
(2,3,1) 2通り
(3,2,1) 1通り
答え 8通り
◆静岡県 ヨッシー さんからのコメント。
答えではありません。
この問題は情報処理などに出てくる、データの並べ替え(ソート)のロジックとよく似ています。
ソートのロジックには色々ありますが、「あみだくじ」は交換法という方法にあたるでしょう。
これは、隣り合う2項を比較し、目的の順序と違っていれば、入れ替えるという方法です。
例えば、問題のような4項のソートをコンピュータで行うときは、
第3項と第4項の比較入れ替えをし、以下
第2項と第3項、第1項と第2項
この時点で第1項が確定
第3項と第4項、第2項と第3項
この時点で第2項が確定
第3項と第4項
これですべて確定
という手順になります。
もし、第1項にあるべきデータが最初第4項にあるとき、各入れ替えによって、順々に第1項まで運ばれてきます。
この様子を泡に例えて、バブルソートとも呼ばれています。
さて、問題の例は、最も多く入れ替えが行われる例ですが、実際は、0と最大入れ替え数の間の回数になります。
その辺を考慮して、入れ替え回数の期待値などというのも問題になるでしょう
(実際ソートロジックの評価には計算されるはず)
以上、余談でした。
◆東京都 未菜実 さんからのコメント。
ヨッシーさんのような方法からのアプローチを私も考えたのですが、阿弥陀では前後関係が問題にならない場合が有り、両者
は等価には、ならないんです。

図のy1とy2の様に。
◆東京都 合屋 さんからの解答。
【問題3】
n=k
横線の本数nC2本。
あみだくじの個数は分かりません。
Ⅰ.右端(An)を左端に移動させる。
これには、右上から左下に階段上に横線を引く必要があり、
これで引いた(n-1)本の横線の数が最小本数である。
Ⅱ.Ⅰの結果(下側)はAn,A1~An-1となり、
(n-1)本の初期状態(A1~An-1)と同じなので 最左端の縦線1本を除いて、Ⅰを行えば結果は
An,An-1,A1~An-2となる。
以下、同じことを繰り返せば全ての入れ替えができる。
それに要する横線の本数は
|
n(n-1) 2 | 本。 |
すなわち、nC2本。
【問題1】
n=4
横線の本数 6本
あみだくじの個数 図に記す8通り
"×n" はこれの類似する個数
( )内の方向に反転させる。
[n]は図形のパターン通番。
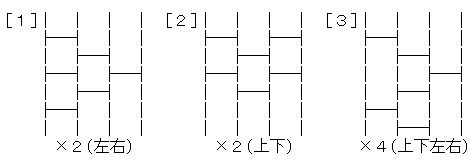
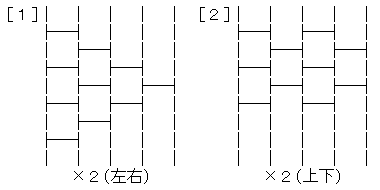
【問題2】
n=5
横線の本数 10本
あみだくじの個数 分かりません。
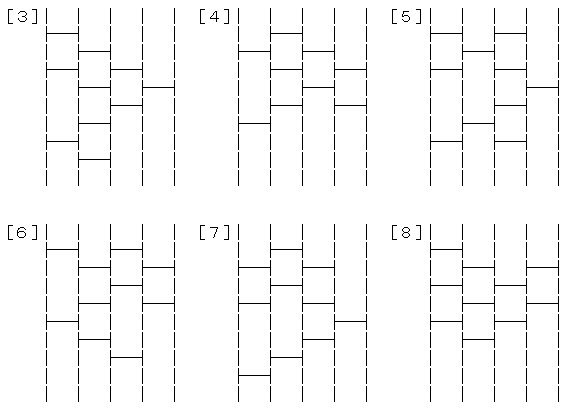
まだあるかも知れませんが、一応見つけた40個を図に記します。
======= 下はすべて ×4(上下左右) =======

◆京都府 釜坂 正芳 さんからの解答。
【問題1-1】
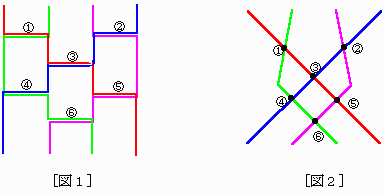
[図1]のように6本で可能です。
[図1]で,a1(赤)~a4(青)がたどる道筋をときほぐすと,[図2]のようになります
[図1]の横線①~⑥は,それぞれ,[図2]の交点①~⑥に対応しています。
最小の横線の数は,上段のa1~a4をそれぞれ下段のa1~a4と2回以上交わらないように,
かつ,同じ点で3本以上が交わらないように結んだときにできる交点の数と一致します。…(ア)
【問題2-1】
(ア)より [図2]のそれぞれの直線に1回ずつ交わるように直線を引くと交点は4つふえるから
6+4=10本
【問題3-1】
敢えて2通りの考え方で,示します。
1) n=kのときの横棒の数(交点の数)をf(k)とすると,
k本目の直線はk-1(本)の直線と交わるから
f(k)=f(k-1)+k-1,f(2)=1 という漸化式ができ,
これから,
| f(k)= |
k(k-1) 2 |
2) k本の直線(折れ線)がそれぞれ1度ずつ,異なる点で交わる時に出来る交点の数は,k本の直線から2本の直線の選び方の数と同じであるから
kC2 で求められる
【問題1-2】
問題文のn=3のときの右側の図を実線で示しています。
それに4本目,青の破線(1)~(4)を加えたのが[図3]です。
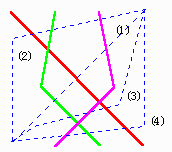
(1)に対応する「あみだくじ」が[図1]で,(2)~(4)は次のようになります。
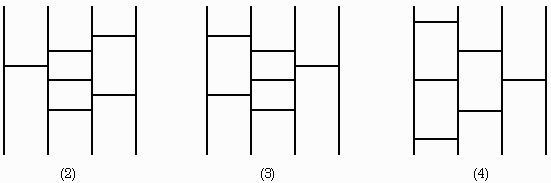
また,問題文n=3の左の図をもとにした場合は,
(1)~(4)を左右,または上下に反転させて得られます。

したがって, 8通り。
【コメント】
しばらく考えていましたが,「あみだくじ」の種類の数は一般形が求められずにいます。
n=5のときを考える気力も亡くしてしまいました。
私はご臨終です。
どなたかの参考になればと,未完成の解答ですが投稿しました。
漸化式になるのか,順列組合せ的に求まるのか,それとも,ヨッシーさんのコメントのように
ほかのアプローチが必要なのか。
どうなんでしょう?
◆広島県 清川 育男 さんからの解答。
【問題2-2】
間違っていました。
プログラムを組んで挑戦しましたが、疲れました。
1,2,3,4->4,3,2,1になるあみだくじの総数(横線の数は最床の条件)を求めて、同型のものを取り除くという考えで臨みました。
視覚的のものをプログラムするのは大変ですね。
クロスマッチングの方法を採用しました。
●排除の条件
10個の数字の列(1,2,3,4)
1は1->2。2は2->3。3は3->4。4は4->5 。。...の部分は同じ文字列。 1)...13.....は、...31.....と同型になる 2)...14.....は、...41.....と同型になる。 3)...24.....は....42.....と同型になる。 4)..124.....は、..142.....と同型になる。 5)..213.....は、..231.....と同型になる。 6)..214.....は、..241.....と同型になる。 7)..314.....は...341.....と同型になる。 8)..324.....は、..342.....と同型になる。 9)..413.....は、..431.....と同型になる。以上を条件に照合しました。
結果は62通りでした。
N=6は908通りが予想されますが...。
答え 62通り。
実際のあみだくじは下記の通りです。
老眼ですが目がひどく疲れました。
1 1213214321
2 1213243212
3 1213432132
4 1214321432
5 1232124321
6 1232143213
7 1232432123
8 1234321232
9 1234321323
10 1243212432
11 1243214323
12 1321324321
13 1321343213
14 1321432143
15 1323432123
16 1324321243
17 1343213243
18 1432132432
19 1432134323
20 1432143243
21 2123214321
22 2123243212
23 2123432132
24 2124321432
25 2132134321
26 2132143214
27 2132343212
28 2132432124
29 2134321324
30 2143213432
31 2143214324
32 2321234321
33 2321243214
34 2321432134
35 2324321234
36 2343212324
37 2343213234
38 2432123432
39 2432124324
40 2432143234
41 3212324321
42 3212343213
43 3212432143
44 3213234321
45 3213243214
46 3213432134
47 3214321343
48 3214321434
49 3234321234
50 3243212343
51 3243212434
52 3432123243
53 3432132343
54 3432132434
55 4321232432
56 4321234323
57 4321243243
58 4321323432
59 4321324324
60 4321343234
61 4321432343
62 4321432434
64個にならなかったのでバグがあるのではとかなり確認しましたが、よくわかりません。
◆東京都 けめ丸 さんからの解答。
あみだくじの種類について考えていました。
一般解が求まらないので公開をためらっていたのですが、「どなたかの参考になれば」という釜坂正芳さんの姿勢に見習い、公開することにしました。
偶然なのか、私も釜坂さんと同じ図を利用しました。
私が数えたところでは、
n=1・・・1通り
n=2・・・1通り
n=3・・・2通り(出題にあった例)
n=4・・・8通り(皆さんと一致)
n=5・・・62通り
当初は、n=5の場合を64通りと予想していたのですが、しらみつぶしに数えてみたら、このようになりました。
数え方に、ちょっと工夫をしています。
釜坂さんの[問題1-2]の解答にある図を用いて説明しましょう。

4本目(破線)が4通り引けることは、次のように分かります。
3本の実線によって7つの領域に分けられていますね。
各領域内に一つずつ点を打ちます。
4本目(破線)は、「右上」の領域から「左下」の領域へと、点を結んで得られます。
ただし、点の結び方にはルールがあります。
(1)必ず実線の「辺」を横切るように結ぶこと。
(2)実線を「右から左へ」と横切る「向き」に進むこと。
各領域内の点(この場合は7つの点)を頂点とした有向グラフを考えるのが便利です。
4本目(破線)の場合の数は、有効グラフの「右上」の頂点から「左下」の頂点への経路の数に等しくなります。
経路の数を求めるには、よくやるように、まず「右上」(スタート)の頂点に1と書きます。
他の頂点には、そこへ移動できる頂点に書かれている数字の和を書いていきます。
最終的に「左下」(ゴール)の頂点に書かれた数字が、経路の数に他なりません
(この場合は4)。
n=3の時の実線図は2種類ありますが、トポロジカルに考えて、その有向グラフは同相になります。
ですから、一方のみ数えて2倍すれば、n=4のあみだくじが8種類あることが分かります。
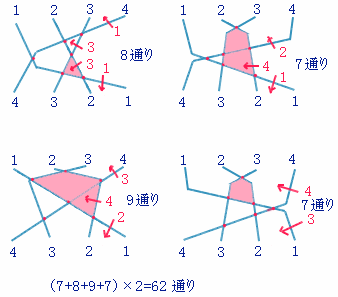
n=5のあみだくじの場合も、同様な作業で求めました。
n=4の8種類の実線図を描き、トポロジカルに異なるもののみを数えたのです。
その結果、
5本目が7通り引けるもの・・・4種類
5本目が8通り引けるもの・・・2種類
5本目が9通り引けるもの・・・2種類
であることが分かりました。
よって、n=5のあみだの種類は、
7×4+8×2+9×2=62通り
#この方法では、n=6はとてもやる気が起きません。(^^;
◆東京都 未菜実 さんからの解答。
場合の数についての検討です。
●n=3の場合

3を両サイドに考えると、
計2通り
●n=4の場合

まず上の図で考えます。
3の時と同様に両サイドに4を考えると、
下の図は上の図と左右対象ですから同じ場合の数になるので
4×2=8通りです。
●n=5の場合
n=4の上の図に対応、
なお、下の図に対応するものは上の図と対称なので同じ場合の数になる。
(左上)
(右上)
(左下)
(右下)
で、結局(8+7×2+9)×2=62通り
しかし、この方法はn=6では24の場合について同じような計算が必要となり限界…。^_^;
◆東京都 未菜実 さんからの解答。
●法則1:
アミダクジの横線は左右の縦線に降りてきたものを入れ替える効果しかありません。
ですから縦線には常に1回、横線には入れ替える際、右からと左からと2回通る事になります。
●法則2:
縦線のn本目とn+1本目の境を考えると、最低、この境を越えて移動しなければならないのは
nとk-nの小さい方の数になります
ですから、最低、その数だけ横線がいる事になります。
また、境を越えなくてはならないもの以外をその境を越えないよう処理すれば、境を越えるのは
最高でも
nとk-nの小さい方の数にすることが出来ます。
●法則3:
ここでanを考えると上段でanの左に存在したものが下段ではanの右に、上段でanの右に存在したも
のは下段ではanの左に来なくてはなりません。
これはnの全てについて言えます。
ですからanは残りの全てと位置を変える必要、つまりその数だけ横線を通る必要があります。
よってk-1本の横線を通ります。
◆広島県 清川 育男 さんからの解答。
十進BASICでプログラミングしました。
2進モードで約2~3倍の速さが得られます。
重複を排除する条件文の配列に工夫しました。
その他高速化のために条件の重複を除きました。
これらによって当初のものより10倍は早くなったと思います。
答えは908通りでした。
横線が(3,6,3,2,1)等はきずきにくいと思います。
例の数列サイトで検索してみました。
以下の通りでした。
ID Number: A006245 (Formerly M1894) Sequence: 1,1,2,8,62,908,24698,1232944,112018190,18410581880 Name: Primitive sorting networks on n elements; also number of rhombic tilings of 2n-gon. References D. E. Knuth, ``Axioms and hulls,'' Lect. Notes Comp. Sci., Vol. 606. See also: Cf. A006246. Keywords: nonn Offset: 1 Author(s): njas Extension: More terms from Sebastien VEIGNEAU (sv@univ-mlv.fr) 1/97.
1 121321432154321 2 121321432543212 3 121321435432132 4 121321454321432 5 121321543215432 6 121324321254321 7 121324321543213 8 121324325432123 9 121324354321232 10 121324354321323 11 121324543212432 12 121324543214323 13 121325432125432 14 121325432154323 15 121343213254321 16 121343213543213 17 121343215432143 18 121343235432123 19 121343254321243 20 121343543213243 21 121345432132432 22 121345432134323 23 121345432143243 24 121354321325432 25 121354321354323 26 121354321543243 27 121432143254321 28 121432143543213 29 121432145432143 30 121432154321543 31 121432435432123 32 121432454321243 33 121432543212543 34 121434543213243 35 121435432132543 36 121454321432543 37 121543214325432 38 121543214354323 39 121543214543243 40 121543215432543 41 123212432154321 42 123212432543212 43 123212435432132 44 123212454321432 45 123212543215432 46 123214321354321 47 123214321543214 48 123214323543212 49 123214325432124 50 123214354321324 51 123214543213432 52 123214543214324 53 123215432135432 54 123215432154324 55 123243212354321 56 123243212543214 57 123243215432134 58 123243254321234 59 123243543212324 60 123243543213234 61 123245432123432 62 123245432124324 63 123245432143234 64 123254321235432 65 123254321254324 66 123254321543234 67 123432123254321 68 123432123543213 69 123432125432143 70 123432132354321 71 123432132543214 72 123432135432134 73 123432154321343 74 123432154321434 75 123432354321234 76 123432543212343 77 123432543212434 78 123435432123243 79 123435432132343 80 123435432132434 81 123454321232432 82 123454321234323 83 123454321243243 84 123454321323432 85 123454321324324 86 123454321343234 87 123454321432343 88 123454321432434 89 123543212325432 90 123543212354323 91 123543212543243 92 123543213235432 93 123543213254324 94 123543213543234 95 123543215432343 96 123543215432434 97 124321243254321 98 124321243543213 99 124321245432143 100 124321254321543 101 124321432354321 102 124321432543214 103 124321435432134 104 124321454321343 105 124321454321434 106 124321543213543 107 124321543215434 108 124324354321234 109 124324543212343 110 124324543212434 111 124325432123543 112 124325432125434 113 124345432123243 114 124345432132343 115 124345432132434 116 124354321232543 117 124354321323543 118 124354321325434 119 124543212432543 120 124543214323543 121 124543214325434 122 125432124325432 123 125432124354323 124 125432124543243 125 125432125432543 126 125432143235432 127 125432143254324 128 125432143543234 129 125432145432343 130 125432145432434 131 125432154323543 132 125432154325434 133 132132432154321 134 132132432543212 135 132132435432132 136 132132454321432 137 132132543215432 138 132134321354321 139 132134321543214 140 132134323543212 141 132134325432124 142 132134354321324 143 132134543213432 144 132134543214324 145 132135432135432 146 132135432154324 147 132143214354321 148 132143214543214 149 132143215432154 150 132143243543212 151 132143245432124 152 132143254321254 153 132143454321324 154 132143543213254 155 132145432143254 156 132154321435432 157 132154321454324 158 132154321543254 159 132343212354321 160 132343212543214 161 132343215432134 162 132343254321234 163 132343543212324 164 132343543213234 165 132345432123432 166 132345432124324 167 132345432143234 168 132354321235432 169 132354321254324 170 132354321543234 171 132432124354321 172 132432124543214 173 132432125432154 174 132432145432134 175 132432154321354 176 132432454321234 177 132432543212354 178 132434543212324 179 132434543213234 180 132435432123254 181 132435432132354 182 132454321243254 183 132454321432354 184 132543212435432 185 132543212454324 186 132543212543254 187 132543214543234 188 132543215432354 189 134321324354321 190 134321324543214 191 134321325432154 192 134321345432134 193 134321354321354 194 134321543214354 195 134323454321234 196 134323543212354 197 134325432124354 198 134354321324354 199 134543213243254 200 134543213432354 201 134543214324354 202 135432132435432 203 135432132454324 204 135432132543254 205 135432134543234 206 135432135432354 207 135432154324354 208 143213243254321 209 143213243543213 210 143213245432143 211 143213254321543 212 143213432354321 213 143213432543214 214 143213435432134 215 143213454321343 216 143213454321434 217 143213543213543 218 143213543215434 219 143214324354321 220 143214324543214 221 143214325432154 222 143214345432134 223 143214354321354 224 143214543214354 225 143215432143543 226 143215432145434 227 143215432154354 228 143234354321234 229 143234543212343 230 143234543212434 231 143235432123543 232 143235432125434 233 143243454321234 234 143243543212354 235 143245432124354 236 143254321243543 237 143254321245434 238 143254321254354 239 143454321324354 240 143543213243543 241 143543213245434 242 143543213254354 243 145432132432543 244 145432134323543 245 145432134325434 246 145432143243543 247 145432143245434 248 145432143254354 249 154321324325432 250 154321324354323 251 154321324543243 252 154321325432543 253 154321343235432 254 154321343254324 255 154321343543234 256 154321345432343 257 154321345432434 258 154321354323543 259 154321354325434 260 154321432435432 261 154321432454324 262 154321432543254 263 154321434543234 264 154321435432354 265 154321454324354 266 154321543243543 267 154321543245434 268 154321543254354 269 212321432154321 270 212321432543212 271 212321435432132 272 212321454321432 273 212321543215432 274 212324321254321 275 212324321543213 276 212324325432123 277 212324354321232 278 212324354321323 279 212324543212432 280 212324543214323 281 212325432125432 282 212325432154323 283 212343213254321 284 212343213543213 285 212343215432143 286 212343235432123 287 212343254321243 288 212343543213243 289 212345432132432 290 212345432134323 291 212345432143243 292 212354321325432 293 212354321354323 294 212354321543243 295 212432143254321 296 212432143543213 297 212432145432143 298 212432154321543 299 212432435432123 300 212432454321243 301 212432543212543 302 212434543213243 303 212435432132543 304 212454321432543 305 212543214325432 306 212543214354323 307 212543214543243 308 212543215432543 309 213213432154321 310 213213432543212 311 213213435432132 312 213213454321432 313 213213543215432 314 213214321454321 315 213214321543215 316 213214324543212 317 213214325432125 318 213214345432132 319 213214354321325 320 213214543214325 321 213215432145432 322 213215432154325 323 213234321254321 324 213234321543213 325 213234325432123 326 213234354321232 327 213234354321323 328 213234543212432 329 213234543214323 330 213235432125432 331 213235432154323 332 213243212454321 333 213243212543215 334 213243214543213 335 213243215432135 336 213243245432123 337 213243254321235 338 213243454321232 339 213243454321323 340 213243543212325 341 213243543213235 342 213245432124325 343 213245432143235 344 213254321245432 345 213254321254325 346 213254321454323 347 213254321543235 348 213432132454321 349 213432132543215 350 213432134543213 351 213432135432135 352 213432154321435 353 213432345432123 354 213432354321235 355 213432543212435 356 213435432132435 357 213454321324325 358 213454321343235 359 213454321432435 360 213543213245432 361 213543213254325 362 213543213454323 363 213543213543235 364 213543215432435 365 214321343254321 366 214321343543213 367 214321345432143 368 214321354321543 369 214321432454321 370 214321432543215 371 214321434543213 372 214321435432135 373 214321454321435 374 214321543214543 375 214321543215435 376 214323435432123 377 214323454321243 378 214323543212543 379 214324345432123 380 214324354321235 381 214324543212435 382 214325432124543 383 214325432125435 384 214345432132435 385 214354321324543 386 214354321325435 387 214543213432543 388 214543214324543 389 214543214325435 390 215432134325432 391 215432134354323 392 215432134543243 393 215432135432543 394 215432143245432 395 215432143254325 396 215432143454323 397 215432143543235 398 215432145432435 399 215432154324543 400 215432154325435 401 232123432154321 402 232123432543212 403 232123435432132 404 232123454321432 405 232123543215432 406 232124321454321 407 232124321543215 408 232124324543212 409 232124325432125 410 232124345432132 411 232124354321325 412 232124543214325 413 232125432145432 414 232125432154325 415 232143213454321 416 232143213543215 417 232143215432145 418 232143234543212 419 232143235432125 420 232143254321245 421 232143543213245 422 232145432134325 423 232145432143245 424 232154321345432 425 232154321354325 426 232154321543245 427 232432123454321 428 232432123543215 429 232432125432145 430 232432154321345 431 232432543212345 432 232435432123245 433 232435432132345 434 232454321234325 435 232454321243245 436 232454321432345 437 232543212345432 438 232543212354325 439 232543212543245 440 232543215432345 441 234321232454321 442 234321232543215 443 234321234543213 444 234321235432135 445 234321254321435 446 234321323454321 447 234321323543215 448 234321325432145 449 234321354321345 450 234321543213435 451 234321543214345 452 234323543212345 453 234325432123435 454 234325432124345 455 234354321232435 456 234354321323435 457 234354321324345 458 234543212324325 459 234543212343235 460 234543212432435 461 234543213234325 462 234543213243245 463 234543213432345 464 234543214323435 465 234543214324345 466 235432123245432 467 235432123254325 468 235432123454323 469 235432123543235 470 235432125432435 471 235432132345432 472 235432132354325 473 235432132543245 474 235432135432345 475 235432154323435 476 235432154324345 477 243212343254321 478 243212343543213 479 243212345432143 480 243212354321543 481 243212432454321 482 243212432543215 483 243212434543213 484 243212435432135 485 243212454321435 486 243212543214543 487 243212543215435 488 243214323454321 489 243214323543215 490 243214325432145 491 243214354321345 492 243214543213435 493 243214543214345 494 243215432134543 495 243215432135435 496 243215432154345 497 243243543212345 498 243245432123435 499 243245432124345 500 243254321234543 501 243254321235435 502 243254321254345 503 243454321232435 504 243454321323435 505 243454321324345 506 243543212324543 507 243543212325435 508 243543213234543 509 243543213235435 510 243543213254345 511 245432123432543 512 245432124324543 513 245432124325435 514 245432143234543 515 245432143235435 516 245432143254345 517 254321234325432 518 254321234354323 519 254321234543243 520 254321235432543 521 254321243245432 522 254321243254325 523 254321243454323 524 254321243543235 525 254321245432435 526 254321254324543 527 254321254325435 528 254321432345432 529 254321432354325 530 254321432543245 531 254321435432345 532 254321454323435 533 254321454324345 534 254321543234543 535 254321543235435 536 254321543254345 537 321232432154321 538 321232432543212 539 321232435432132 540 321232454321432 541 321232543215432 542 321234321354321 543 321234321543214 544 321234323543212 545 321234325432124 546 321234354321324 547 321234543213432 548 321234543214324 549 321235432135432 550 321235432154324 551 321243214354321 552 321243214543214 553 321243215432154 554 321243243543212 555 321243245432124 556 321243254321254 557 321243454321324 558 321243543213254 559 321245432143254 560 321254321435432 561 321254321454324 562 321254321543254 563 321323432154321 564 321323432543212 565 321323435432132 566 321323454321432 567 321323543215432 568 321324321454321 569 321324321543215 570 321324324543212 571 321324325432125 572 321324345432132 573 321324354321325 574 321324543214325 575 321325432145432 576 321325432154325 577 321343213454321 578 321343213543215 579 321343215432145 580 321343234543212 581 321343235432125 582 321343254321245 583 321343543213245 584 321345432134325 585 321345432143245 586 321354321345432 587 321354321354325 588 321354321543245 589 321432134354321 590 321432134543214 591 321432135432154 592 321432143454321 593 321432143543215 594 321432145432145 595 321432154321454 596 321432154321545 597 321432343543212 598 321432345432124 599 321432354321254 600 321432434543212 601 321432435432125 602 321432454321245 603 321432543212454 604 321432543212545 605 321434543213245 606 321435432132454 607 321435432132545 608 321454321343254 609 321454321432454 610 321454321432545 611 321543213435432 612 321543213454324 613 321543213543254 614 321543214345432 615 321543214354325 616 321543214543245 617 321543215432454 618 321543215432545 619 323432123454321 620 323432123543215 621 323432125432145 622 323432154321345 623 323432543212345 624 323435432123245 625 323435432132345 626 323454321234325 627 323454321243245 628 323454321432345 629 323543212345432 630 323543212354325 631 323543212543245 632 323543215432345 633 324321234354321 634 324321234543214 635 324321235432154 636 324321243454321 637 324321243543215 638 324321245432145 639 324321254321454 640 324321254321545 641 324321454321345 642 324321543213454 643 324321543213545 644 324324543212345 645 324325432123454 646 324325432123545 647 324345432123245 648 324345432132345 649 324354321232454 650 324354321232545 651 324354321323454 652 324354321323545 653 324543212343254 654 324543212432454 655 324543212432545 656 324543214323454 657 324543214323545 658 325432123435432 659 325432123454324 660 325432123543254 661 325432124345432 662 325432124354325 663 325432124543245 664 325432125432454 665 325432125432545 666 325432145432345 667 325432154323454 668 325432154323545 669 343212324354321 670 343212324543214 671 343212325432154 672 343212345432134 673 343212354321354 674 343212543214354 675 343213234354321 676 343213234543214 677 343213235432154 678 343213243454321 679 343213243543215 680 343213245432145 681 343213254321454 682 343213254321545 683 343213454321345 684 343213543213454 685 343213543213545 686 343215432134354 687 343215432143454 688 343215432143545 689 343234543212345 690 343235432123454 691 343235432123545 692 343254321234354 693 343254321243454 694 343254321243545 695 343543212324354 696 343543213234354 697 343543213243454 698 343543213243545 699 345432123243254 700 345432123432354 701 345432124324354 702 345432132343254 703 345432132432454 704 345432132432545 705 345432134323454 706 345432134323545 707 345432143234354 708 345432143243454 709 345432143243545 710 354321232435432 711 354321232454324 712 354321232543254 713 354321234543234 714 354321235432354 715 354321254324354 716 354321323435432 717 354321323454324 718 354321323543254 719 354321324345432 720 354321324354325 721 354321324543245 722 354321325432454 723 354321325432545 724 354321345432345 725 354321354323454 726 354321354323545 727 354321543234354 728 354321543243454 729 354321543243545 730 432123243254321 731 432123243543213 732 432123245432143 733 432123254321543 734 432123432354321 735 432123432543214 736 432123435432134 737 432123454321343 738 432123454321434 739 432123543213543 740 432123543215434 741 432124324354321 742 432124324543214 743 432124325432154 744 432124345432134 745 432124354321354 746 432124543214354 747 432125432143543 748 432125432145434 749 432125432154354 750 432132343254321 751 432132343543213 752 432132345432143 753 432132354321543 754 432132432454321 755 432132432543215 756 432132434543213 757 432132435432135 758 432132454321435 759 432132543214543 760 432132543215435 761 432134323454321 762 432134323543215 763 432134325432145 764 432134354321345 765 432134543213435 766 432134543214345 767 432135432134543 768 432135432135435 769 432135432154345 770 432143234354321 771 432143234543214 772 432143235432154 773 432143243454321 774 432143243543215 775 432143245432145 776 432143254321454 777 432143254321545 778 432143454321345 779 432143543213454 780 432143543213545 781 432145432134354 782 432145432143454 783 432145432143545 784 432154321343543 785 432154321345434 786 432154321354354 787 432154321434543 788 432154321435435 789 432154321454345 790 432154321543454 791 432154321543545 792 432343543212345 793 432345432123435 794 432345432124345 795 432354321234543 796 432354321235435 797 432354321254345 798 432434543212345 799 432435432123454 800 432435432123545 801 432454321234354 802 432454321243454 803 432454321243545 804 432543212343543 805 432543212345434 806 432543212354354 807 432543212434543 808 432543212435435 809 432543212454345 810 432543212543454 811 432543212543545 812 434543212324354 813 434543213234354 814 434543213243454 815 434543213243545 816 435432123243543 817 435432123245434 818 435432123254354 819 435432132343543 820 435432132345434 821 435432132354354 822 435432132434543 823 435432132435435 824 435432132454345 825 435432132543454 826 435432132543545 827 454321232432543 828 454321234323543 829 454321234325434 830 454321243243543 831 454321243245434 832 454321243254354 833 454321323432543 834 454321324324543 835 454321324325435 836 454321343234543 837 454321343235435 838 454321343254345 839 454321432343543 840 454321432345434 841 454321432354354 842 454321432434543 843 454321432435435 844 454321432454345 845 454321432543454 846 454321432543545 847 543212324325432 848 543212324354323 849 543212324543243 850 543212325432543 851 543212343235432 852 543212343254324 853 543212343543234 854 543212345432343 855 543212345432434 856 543212354323543 857 543212354325434 858 543212432435432 859 543212432454324 860 543212432543254 861 543212434543234 862 543212435432354 863 543212454324354 864 543212543243543 865 543212543245434 866 543212543254354 867 543213234325432 868 543213234354323 869 543213234543243 870 543213235432543 871 543213243245432 872 543213243254325 873 543213243454323 874 543213243543235 875 543213245432435 876 543213254324543 877 543213254325435 878 543213432345432 879 543213432354325 880 543213432543245 881 543213435432345 882 543213454323435 883 543213454324345 884 543213543234543 885 543213543235435 886 543213543254345 887 543214323435432 888 543214323454324 889 543214323543254 890 543214324345432 891 543214324354325 892 543214324543245 893 543214325432454 894 543214325432545 895 543214345432345 896 543214354323454 897 543214354323545 898 543214543234354 899 543214543243454 900 543214543243545 901 543215432343543 902 543215432345434 903 543215432354354 904 543215432434543 905 543215432435435 906 543215432454345 907 543215432543454 908 543215432543545所要時間約10時間。
清川さんにお願いして、プログラムを公開していただきました。
◆広島県 清川 育男 さんからの解答。
一般性もなく、構造化プログラミングになっていないので、公開するのは恥ずかしいのですが。
高速化の工夫はしていると思います。
DIM A(6)
DIM D(300000)
LET C=0
LET Z=1
FOR I=1 TO 6
LET A(I)=I
NEXT I
FOR I1=1 TO 5
SWAP A(I1),A(I1+1)
FOR I2=1 TO 5
IF I2=I1 THEN 200
SWAP A(I2),A(I2+1)
FOR I3=1 TO 5
IF I3=I2 THEN 190
SWAP A(I3),A(I3+1)
FOR I4=1 TO 5
IF I4=I3 THEN 180
IF I1=I3 AND I2=I4 THEN 180
SWAP A(I4),A(I4+1)
FOR I5=1 TO 5
IF I5=I4 THEN 170
IF I2=I4 AND I3=I5 THEN 170
SWAP A(I5),A(I5+1)
FOR I6=1 TO 5
IF I6=I5 THEN 160
IF I3=I5 AND I4=I6 THEN 160
SWAP A(I6),A(I6+1)
FOR I7=1 TO 5
IF I7=I6 THEN 150
IF I4=I6 AND I5=I7 THEN 150
SWAP A(I7),A(I7+1)
FOR I8=1 TO 5
IF I8=I7 THEN 140
IF I5=I7 AND I6=I8 THEN 140
SWAP A(I8),A(I8+1)
FOR I9=1 TO 5
IF I9=I8 THEN 130
IF I6=I8 AND I7=I9 THEN 130
SWAP A(I9),A(I9+1)
FOR I10=1 TO 5
IF I10=I9 THEN 120
IF I7=I9 AND I8=I10 THEN 120
SWAP A(I10),A(I10+1)
FOR I11=1 TO 5
IF I11=I10 THEN 110
IF I8=I10 AND I9=I11 THEN 110
SWAP A(I11),A(I11+1)
FOR I12=1 TO 5
IF I12=I11 THEN 100
IF I9=I11 AND I10=I12 THEN 100
SWAP A(I12),A(I12+1)
FOR I13=1 TO 5
IF I13=I12 THEN 90
IF I10=I12 AND I11=I13 THEN 90
SWAP A(I13),A(I13+1)
FOR I14=1 TO 5
IF I14=I13 THEN 80
IF I11=I13 AND I12=I14 THEN 80
SWAP A(I14),A(I14+1)
FOR I15=1 TO 5
IF I15=I14 THEN 70
IF I12=I14 AND I13=I15 THEN 70
SWAP A(I15),A(I15+1)
IF A(1)=6 AND A(2)=5 AND A(3)=4 AND A(4)=3 AND A(5)=2 THEN
LET C=C+1
LET E=0
LET D(C)=I1*100000000000000+I2*10000000000000+I3*1000000000000+I4*100000000000+I5*10000000000+I6*1000000000+I7*100000000+I8*10000000+I9*1000000+I10*100000+I11*10000+I12*1000+I13*100+I14*10+I15
IF C=1 THEN
PRINT 1;D(1)
GOTO 60
END IF
FOR I=C-1 TO 1 STEP -1
LET X=D(C)-D(I)
IF X=18 OR X=27 OR X=36 OR X=180 OR X=270 OR X=360 OR X=1800 OR X=2700 OR X=3600 OR X=18000 OR X=27000 OR X=36000 OR X=180000 OR X=270000 OR X=360000 OR X=1800000 OR X=2700000 OR X=3600000 OR X=18000000 OR X=27000000 OR X=36000000 OR X=180000000 OR X=270000000 OR X=360000000 OR X=1800000000 OR X=2700000000 OR X=3600000000 OR X=18000000000 OR X=27000000000 OR X=36000000000 OR X=180000000000 OR X=270000000000 OR X=360000000000 OR X=1800000000000 OR X=2700000000000 OR X=3600000000000 OR X=18000000000000 OR X=27000000000000 OR X=36000000000000 OR X=180000000000000 OR X=270000000000000 OR X=360000000000000 THEN
LET I=1
LET E=1
END IF
NEXT I
IF E=0 THEN
LET Z=Z+1
PRINT Z;D(C)
END IF
END IF
60 SWAP A(I15),A(I15+1)
70 NEXT I15
SWAP A(I14),A(I14+1)
80 NEXT I14
SWAP A(I13),A(I13+1)
90 NEXT I13
SWAP A(I12),A(I12+1)
100 NEXT I12
SWAP A(I11),A(I11+1)
110 NEXT I11
SWAP A(I10),A(I10+1)
120 NEXT I10
SWAP A(I9),A(I9+1)
130 NEXT I9
SWAP A(I8),A(I8+1)
140 NEXT I8
SWAP A(I7),A(I7+1)
150 NEXT I7
SWAP A(I6),A(I6+1)
160 NEXT I6
SWAP A(I5),A(I5+1)
170 NEXT I5
SWAP A(I4),A(I4+1)
180 NEXT I4
SWAP A(I3),A(I3+1)
190 NEXT I3
SWAP A(I2),A(I2+1)
200 NEXT I2
SWAP A(I1),A(I1+1)
210 NEXT I1
END◆東京都 合屋 さんからの解答。
『少し説明』
NESTが入れ子です。
最初はMAINから呼び出し、後は入れ子の深さだけNESTがNESTを呼びます。
NESTのパラメータ DPは入れ子の深さ、
SVはNESTの中で使っているFORの制御変数(IDX)を復元するためのsave
入れ子の中で使用する変数で入れ子の深さによって異なる値を持つ変数(ここではIX)は深さを添え字にした配列にしておけば良いのですが、FORの制御変数には配列が 使用できないのでFUNCTIONを抜ける時に値を戻して引き継ぎます。
●青木注
プログラムはCopy & Paste してお使いください。
REM 『あみだくじ』 十進BASIC
! A(1)~A(n)をA(n)~A(1)に並べ替える横線のパターンを生成する。
OPTION BASE 0
SET ECHO "OFF"
DO
INPUT PROMPT "縦線の数 Nは": K
LOOP WHILE K<3 OR K>9
PRINT TIME$;" 開始"
DIM A(1 TO K)
LET YOKO=K*(K-1)/2 ! 横線の数
PRINT "N=";K;"のパターンリスト"
PRINT "横線が";YOKO;"本引かれます"
PRINT
PRINT "通番 横線の位置"
DIM IX(0 TO YOKO) ! 添字:横線番号(上からn番目の横線)
! 値 :横線の位置(A(値)とA(値+1)の間
LET K=K-1
LET C=0
CALL IXINI
LET IDX=NEST(1,1)
PRINT TIME$;" 終了"
STOP
10 FUNCTION NEST(DP,SV)
IF C=0 THEN
LET S=IX(DP)
ELSE
IF IX(DP-1)<3 THEN LET S=1 ELSE LET S=IX(DP-1)-1
END IF
FOR IDX=S TO K
LET IX(DP)=IDX
IF IDX=IX(DP-1) THEN 98
SWAP A(IDX),A(IDX+1)
IF DP<YOKO THEN
LET IDX=NEST(DP+1,IDX)
GOTO 97
END IF
IF C=0 THEN
CALL AINI
ELSE
FOR XX=1TO K
IF A(XX)<>K+2-XX THEN 97
NEXT XX
END IF
LET C=C+1
LET P$=""
FOR Z=1 TO YOKO
LET P$=P$&STR$(IX(Z))
NEXT Z
PRINT USING "##### "&P$: C
97 SWAP A(IDX),A(IDX+1)
98 NEXT IDX
LET NEST=SV
END FUNCTION
! 1st Pattern Setting
SUB IXINI
LET L=1
FOR XX=1 TO K
FOR YY=XX TO 1 STEP -1
LET IX(L)=YY
LET L=L+1
NEXT YY
NEXT XX
END SUB
SUB AINI
FOR XX=1 TO K+1
LET A(XX)=K+2-XX
NEXT XX
END SUB
END