◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】 必ずいる。
背理法で証明する。
いないとすると最大の挨拶数はn−1回だからn人の挨拶数がすべて異なる組み合わせは
0,1,...,n−1 のただ1とおりである。
最大のn-1回挨拶した人:Aと、その他の人(n-1人)に分けると、その他の人はもう一回Aとは挨拶できないと同時に全てAと一回ずつ挨拶しており、Aの存在を無視しても同じである。
よって問題はn-1人の問題に還元される。
以上繰り返すとn=2 に還元され、この二人の挨拶数が異なることは無い。
よって、必ず同じ挨拶数の人がいる。
【問題2】 起こりうる。
人数をn=101、検査グループ数をg=11、
最大挨拶数をm=9 とし、背理法で証明する。
ある挨拶の組み合わせで、どの検査グループにも挨拶済みがいるとする。
この時、少なくとも1人の挨拶数がm回であるとしてよい。
もし最大がm未満なら、m回の人が現れるまで挨拶をしても、やはりどの検査グループにも挨拶済みがいるからである。
このときn人を m回挨拶した1人:A と
Aと挨拶したm人のグループ:Bと
その他のn−m−1人のグループ:Cの3つに分ける。
すると AとCのみからなるg人の検査グループにも少なくとも一組挨拶済みのペアがいる。
ただし、AはBグループとのみ挨拶しているから、
結局Cのグループ内のg−1人の検査グループ内に少なくとも1組挨拶済みがいる。
C内の1人の挨拶数は前と同様にm回としてよく、
問題は n=n−m−1、g=g−1、m=m の問題に還元できる。
以上を繰り返すと最終的に
n=101→91→81→71→61→51→41→31→21→11
g= 11→10→ 9→ 8→ 7→ 6→ 5→ 4→ 3→ 2
m=9
の問題となる。
11人から任意の2人が挨拶済みであるということは、全てのペアが挨拶していることである。
即ち1人10回挨拶している。
これはm=9と矛盾する。
よって起こりうるといえる。
【問題3】 228組
全人数をnとします。
n=60の場合の最小ペア数(=M)をあたえる挨拶パターンにおいて、
最も多く挨拶した人の一人をAとし、その挨拶数をmAとします。
そこで、このAが入らない8人組を考えると、
A以外の59人がM−mA回の挨拶をしている状態で、任意の8人組において挨拶をしたペアがいる必要があります。
よって、mAはなるべく小さい方が有利であり、小さくて損になることはない。
一方最大の挨拶数を7とすると問題2の方法で破綻することがわかるので、
mA=8としてよい。
n=59に対しても最大7回は破綻するのでmB=8。
以上を繰り返すと、n=56でm=7は破綻しなくなります。
さらに繰り返すと下記の列が得られ、mの総合計は
4×(1から8までの和)+3×(1から7までの和)=228
になります。よって228ペアが最小です。
n =60 59 58 57 56 55 54 53 52 51 50 49 … 43 42…36 35…29 28…22 21… m = 8 8 8 8 7 7 7 7 7 7 7 6 … 6 5… 5 4… 4 3… 3 2…具体的には、nをなるべく同じ人数の7(=8-1)グループに分け、各グループ内では全員が挨拶済みであれば条件を満足します。
すなわち 60=4×9+3×8 なので
4×9C2+3×8C2=228
は最小値に一致しています。
【おまけ】
n人のグループをそれぞれA,Bとする。
問題となる3人組は互いに知り合いなので、AまたはBからだけではできない。
すなわち、Aから隣接2人とBから任意に1人 またはA⇔Bしたものである。
背理法により証明する。
少なくとも1組だけ異なる挨拶があるとする。
この場合、Aのグループ間とBのグループ間で異なる挨拶が必ずあり、これを
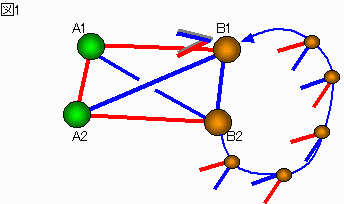
A1-A2 と B1−B2 とする。図1参照。
するとここで問題となる3人組は
A1-A2-B1、A1-A2-B2、B1-B2-A1、B1-B2-A2
の4つである。
条件を満足する挨拶言葉の組み合わせは B1-B2の順番を無視すると図1の一通りである。
図中 赤線はA1-A2の挨拶言葉、青線はB1-B2間の挨拶言葉とする。
図から判る様に、A1-B1間は赤で A1-B2間は青である。
もしBグループ間の挨拶言葉が全部同じなら
A1-B3は赤、A1-B4は青に限られ以下、赤青は交互に現れなければならない。
ところがnは奇数であるため一周してくると偶奇性が矛盾する。
よって、Bグループ内は(全てが同じ挨拶言葉)ではない。
Aグループも同様である。

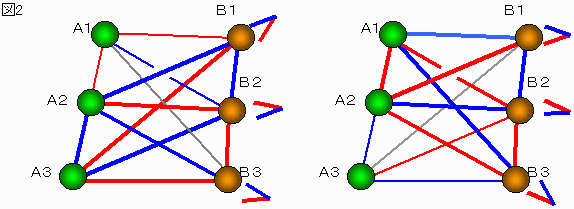
以上より各グループ内連絡網に 図2のような挨拶言葉が変わる部分がある。
これをA1-A2-A3、B1-B2-B3 とする。
そしてこの間の挨拶の可能性を考えると、図2に示す2通りが残る。
これらは対称であり、実質1とおりである。
なお灰色線は赤でも青でも良いことを表す。
先の証明と同様 A1-A2ないしA2-A3を中心軸としてBグループ側間が同じ挨拶言葉(色)が続くと偶奇性が合わず矛盾する。
よって、途中で挨拶言葉はさらに連絡網のなかで沢山変わらなければならい。
しかし、その変化点でも図2と同じ状況であるから、
A1-A2ないしA2-A3を中心軸としたA−B間の挨拶の偶奇性は維持され、一周すると矛盾する。
よって仮定は誤りであり、2n組みの挨拶言葉は全部同じである。
【出題者のコメント】
解答ありがとうございます。
2ヶ月以上も解答がなかったので、とても嬉しいです。
すべて正解です。
しかも、どれもとても解り易く思えます。
【問題1】は「鳩の巣箱の原理」を利用しても以下のように証明できます。
n人の参加者おのおのに挨拶した人数を申告してもらうと、
0人〜(n−1)人のn通りの内のいずれかを得ます。
それを集計すると最大n種類の挨拶人数があるように思えますが、
0人とn−1人の申告が同時に存在することはありえません。
よって、n人の参加者の集計では高々n−1種類の挨拶人数しかありません。
n人のおのおのがそのいずれかに属するので、どうしても何処かの挨拶人数には2人以上がいなければなりません。
【問題2】,【問題3】は各参加者をそれぞれの点に2人で交わす挨拶を2点を結ぶ線にするとグラフ理論になります。
ただし、同一の2点間を結ぶ線は2本以上はないものとします。
【問題2】を一般化させると、mn+1個の各点の間では以下の(1),(2)のいずれかが成立します。
(1)m個以上の点と線で結ばれている点が少なくとも1個存在する。
(2)あるn+1個の点同士の間では互いにどの点とも線で結ばれていない。
【問題3】を一般化させると、次のようになります。(テュランの定理)
互いにどの2点も線で結ばれていない点の最大集団があり、その集団の点の個数が高々n個である時、
それらを含むmn+r(0≦r<n)個の点の間では、2点を結んだ線は少なくとも
rm+1C2+(n−r)mC2 本存在する。