◆千葉県 なのはな子 さんからの解答。
【問題1】
(1)正四面体
【問題1】
(2)正八面体

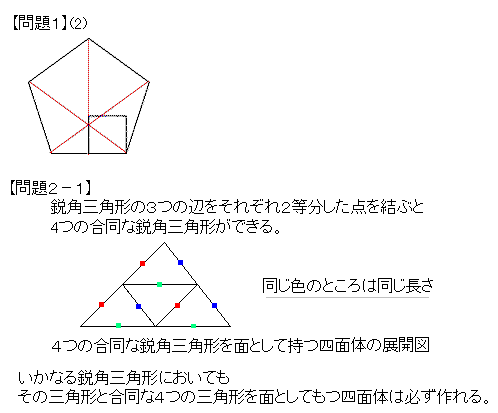
【問題2−2】
【感想】
実際に描いて確かめることはできませんが、なんとなく描けそうな気がします。
空間では3面が交われば1点が決まるのではないか?……と考えてみました。
「面が交わる」ことも、空間に空気クレヨンなら不可能ではないような気がしました。
◆東京都の中学校3年生 もやし さんからの解答。
【準備】
任意の平面上の点Pにおけるその平面に垂直な直線の作図
(1) 任意の平面上の点Pで直交する2直線l、mをひく。
(2) 点Pにおけるmと一致しないlの垂線をひく。
(3) (2)の直線上に任意の点Qをとり、Qからmに垂線QHを下ろす。
(4) Pを通りQHに平行な直線をひく。
これを<面の垂線の作図>と呼ぶことにする。
【問題1】
(1)正四面体
(1) <面の垂線の作図>を駆使して立方体をかく。
(2) 図のように4点を選び、結ぶと正四面体になる。
(2)正八面体
(1) <面の垂線の作図>を駆使して立方体をかく。
(3)正十二面体
(1) 正五角形ABCDEと対角線BEを一辺とする正方形を辺CD側にかく。
(4)正二十面体
(1) 上記のように正十二面体をかく。 【問題2−1】
任意の直方体で、【問題1】の(1)のような結び方をすれば、全ての面が合同な四面体ができる。
【問題2−2】
上の図は、∠BAC=∠CAD=∠DAB=90°の四面体、
BからCDに垂線BPを下ろして、AとPを結ぶと、AP⊥CDとなる。
面ABP,ACQ,ADRは全て△BCDに垂直な面で、3つともAHで交わっている。
(1) 空間にあたえられた鋭角三角形の頂点を反時計回りにB,C,Dとし、B,CからCD,DBに垂線BP,CQをそれぞれ下ろす。
(2) <面の垂線の作図>を用いてHを通り△BCDに垂直な直線をひく。
(3) (2)の直線上にBM=AMとなるような点Aをとり、三角錐A-BCDをつくる。
(4) <面の垂線の作図>を利用して、AB,AC,ADを辺とする直方体をかき、図のように結ぶと、求める四面体ができる。
【感想】
立方体は便利なものですね。
(2) 図のように各面の中心を結ぶと、正八面体になる。
(2) <面の垂線の作図>を駆使して(1)の正方形を1つの面とする立方体をかく。
(3) C,DからBEに垂線CP,DQを下ろし、CP,DQの延長とBEの対辺との交点をR,Sとする。
(4) PR,QSの中点をM,Nとし、<面の垂線の作図>を用いてM,Nを通り四角形PRSQに垂直な直線をひく。
(5) (4)の直線のうちMを通るほうにBC=BXとなるような点Xをとり、Nを通るほうにED=EYとなるような点Yをとる。
(6) 向きに注意しながら(3)〜(5)の作業を他の全ての面でもやると、正十二面体ができる。
(2) 正十二面体の各面の中心を辺の垂直二等分線などでとり、図のように結ぶと正二十面体ができる。
したがって、いかなる鋭角三角形においても,その三角形と合同な4つの三角形を面としてもつ四面体が必ず作れる。
つまり【問題2−1】の直方体の角っこです。
C,DからDB,BCに垂線を下ろしても同様である。
その足をそれぞれQ,Rとし、△BCDの垂心をHとする。
したがって、頂点Aから△BCDに下ろした垂線は、点Hで△BCDと交わる。
これを利用する。
また、△BCDの垂心をHとし、BPの中点Mをとる。
正多面体の包含関係はきれいなものです。
余談ですが、包含関係を利用して正十二面体、正二十面体の体積を求めることができますね。