◆広島県 清川 育男 さんからの解答。
以前出題された『6人の村人』という問題を連想しました。
現在、試行錯誤でさがしています。
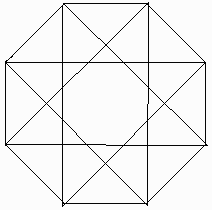
八角形の頂点を反時計回りに、A,B,C,D,E,F,G,Hとする。
AB,BC,CD,DE,EF,FG,GH,BD,DF,FH,HBを青線とする。
このとき、
ACE,ACF,ACG,ADG,AEG,BEG,CEG,CEH,CFHの9個が三辺が赤線の三角形となる。
いまのところ最小値は9個です。
アイデアが浮かびません。
【出題者のコメント】
初めから最小値を設定して問題を出そうかどうか悩んだのですが、この手の問題は、あらかじめ最小値がわかってしまうと、その値を気にしながら証明になってしまうので、自分ではなかなか気づかない欠陥が生じることが良くあります。
(かくいう私もそう (^^))
そこで最小値はみなさんに考えてもらうことにしました。
実はこの問題はみかけによらず難しいことに気づかれるかと思います。
私も(自分自身で納得できるような)エレガントな解法は見つかっていないので、みなさんの発想力(アイディア)にゆだねようということで出題しました。
(あっ、これって前回と同じパターンだ!(笑))
ヒントですが最小値は9よりももっと小さいです。
◆三重県 久保田 尚 さんからの解答。
いい方法が思いつかないので、試行錯誤で考えました。
まず、正8角形の各頂点を8つの点と考えます
(各辺がすでに8本ある)
次に、適当な点から時計周りに点を2つとばすように順番に線を引いていきます。
すると8本引いて元の点に戻ってきます。
これで16本の線が引けたことになり、まだ3角形は1つもありません。
(形としては長方形が縦横斜めに4つクロスする形になっているはずです)
最後の17本目の線ですが、16本まで引いた形が完全な対称形なので、どの点で考えてもいいことになります。
ある点から17本目の線を引く形は、1つとばしか、3つとばし(ちょうど反対の点)のどちらかですが、どちらに引いたとしても3角形が4つできます。
ということで最小の数は、4つだと思います。
【コメント】
図を書いて考えてみたのですが、三角形がたくさんできてしまいました。
私の勘違いだと思うのですが、どこがおかしいのでしょう。

◆三重県 久保田 尚 さんからのコメント。
回答ではなく、確認の質問なんですが、この問題の三角形とは「8つの頂点のうち3つを結ぶ三角形」という意味ではないのでしょうか?
清川さんの答えを図に書いて確認してもそういう意味だったので、ボクもそう理解していましたが・・・
もし、3本の線に囲まれた三角形の事を意図しているとすると、根本から考え直さないといけなくなるので、出題者の方のコメントをお待ちしています。
【出題者のコメント】
一見たくさんありそうですが、よく見てみると………
8つの点のある点(どこでもいい)からはじまって1,2,3,……,8と番号を振っていきます。
今、それらの点を偶奇で分類したとき、偶奇が一致する2点間は決して赤線分が存在していないことに注意すると、任意に3点を選んだとき、どうしても偶奇が一致する2点を選ばざるを得ないので、久保田さんの16本の引き方では赤い三角形は現れてこないと思います。
(実際に上記の16本の引き方の傘下で17本の引き方を構成したことで最小値は4以下だとわかるのですが、でもここからが山場なんですよね。
下から値を押さえる作業(=最小値が3以下にならないことの証明)がけっこう大変(^^;))
◆広島県 清川 育男 さんからの解答。
久保田さんの解答とAsamiさんのヒントをもとに考えました。
8点を1,2,3,4,5,6,7,8と番号を付ける。
奇数番と偶数を赤線で結ぶ。
この場合の数は、
4C1×4C1=16。
この時点でどの3点をとっても3辺が赤線で結ばれた三角形は存在しない。
(その理由)
3点を偶数、奇数で分類する。
1)偶数番、偶数番、偶数番 (偶数番3個)
2)偶数番、偶数番、奇数番 (偶数番2個、奇数番1個)
3)奇数番、奇数番、偶数番 (偶数番1個、奇数番2個)
4)奇数番、奇数番、奇数番 (奇数番3個)
1)、4)は存在しない。
2)、3)の場合
偶数番−偶数番、奇数番−奇数番は結ばれていないので、3点が赤線で結ばれた三角形は存在しない。
残り1本の赤線の取り方。
1−3 2−4
1−5 2−6
1−7 2−8
3−5 4−6
3−7 4−8
5−7 6−8
これらは2群に分類される。
1群(8角形の頂点に点を取った場合 頂点を1個とばした結び方)
1−3 2−4
1−7 2−8
3−5 4−6
5−7 6−8
2群(8角形の頂点に点を取った場合 頂点を3個とばした結び方)
1−5 2−6
3−7 4−8
1群の場合 4個
2群の場合 3個
この場合は最小値3個となる。
この場合以外での結び方では16本で少なくとも2個できる。
残り1本を加えたとき少なくとも1個以上増えるので最小値は3個となる。
答え 3個。
偶然にも最初に漠然と考えた根拠のない数と一致しました。
◆広島県 清川 育男 さんからの解答。
また間違えました。
解答の2群も4個でした。
結局、久保田さんの解答を確認しただけでした。
◆東京都 合屋 さんからの解答。
三角形を作らずに2点間を結ぶことを考えると,8つの点は同じ条件下にあるため、8つの点に任意の順に1〜8の番号を割り振って、1の点と結ぶ線を決め、次に2の点と結ぶ線を決めるというように順次結んでいきます。
まず、1の点を基点として、2〜8の点に結びます。
以下では、これを
1=>2,3,4,5,6,7,8
と表します。
2の点から1の点へは既に結んであります。
以下では、これを
2=>(1)
と表します。
この状態では1から結ぶ点は無く、2〜8の点はすべて1と結ばれているため、2〜8のどの2点を結んでも1との間で三角形ができます。
このように結び方を考えていくと、線の結び方は以下の4つのケースになります。
●ケース1(1から7本)
1=>2,3,4,5,6,7,8
2=>(1)
3=>(1)
4=>(1)
5=>(1)
6=>(1)
7=>(1)
8=>(1)
線の数=7
●ケース2(1から6本)
1=>2,3,4,5,6,7
2=>(1,)8
3=>(1,)8
4=>(1,)8
5=>(1,)8
6=>(1,)8
7=>(1,)8
8=>(1,7)
線の数=12
●ケース3(1から5本)
1=>2,3,4,5,6
2=>(1,)7,8
3=>(1,)7,8
4=>(1,)7,8
5=>(1,)7,8
6=>(1,)7,8
7=>(2,3,4,5,6)
8=>(2,3,4,5,6)
線の数=15
●ケース4(1から4本)
1=>2,3,4,5
2=>(1,)6,7,8
3=>(1,)6,7,8
4=>(1,)6,7,8
5=>(1,)6,7,8
6=>(2,3,4,5)
7=>(2,3,4,5)
8=>(2,3,4,5)
線の数=16
・注
1からの線が3,2,1本の場合はケース3〜1を番号の順序を変えたものであり、その他の結び方も同様に番号を並べ変えたものになる。
(久保田さんからの解答中の図はケース4)
そうで無ければ、三角形ができているか、三角形を作らずに結べる線がある。
以下の図はケース4の一例である。
(点の位置、番号の振り方は任意なのでこのような点の配置であっても三角形を作らずに16本結べる)
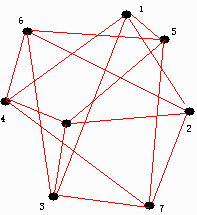
本来の問題は17本の線を結んだ場合であるから、ケース4に於いてはもう1本結ぶ必要がある。
ここで例えば2と3を結ぶと1と2および1と3は既に結んであるから1−2−3を頂点とする三角形ができる。
これは1を基点とする時の右辺に2も3もあることをチェックすることで確認できる。1=>2,3,4,5
〜 〜 〜
この確認方法で右辺に2と3の両方を含む基点を探すと1、6,7,8の4つがあるので2と3を結べば4つの三角形ができることが分かる。
ケース4ではどの2点を結んでも4つの三角形ができます。
ケース3の場合は既に15本結んであるから、あと2本結ぶことになる。
いずれか2点を結び線を1本増やすと3つの三角形ができる。
もう1本結ぶとさらに3つでき、計6つの三角形ができる。
ケース1および2ではそれぞれ10本と5本の線を増やすことになるが、1本結ぶと最低1つの三角形ができるので少なくとも5つ以上の三角形ができる。
よって、それぞれの点から4本の線が出るように結んだケース4に1本加えた線の結び方の時が最低で4つの三角形ができる。