y=1/
y=−1/
◆鹿児島県 ともひろ さんからの解答。
【作図方法】
△ABCにおいて、線分ABの垂直二等分線を引く。
また線分ABの中点を点Mとする。
点Mを中心、半径をAM(BM)とする円を描く。
上記の線分ABの垂直二等分線と、この円の交点(三角形ABCの外側)を点M’とする。
この点M’を中心、半径をAM(BM)とする円を描く。
二つの円の交点を、A’、B’とする。
ここで、△AM’M、△BM’Mは正三角形となる。
線分A’M・B’Mに平行で、それぞれ点A、点Bを通る直線を引く。
線分ABの垂直二等分線との交点をM''とする。
ここで、A’M//AM''、B’M//BM''であるから、
∠AM''M=∠A’MM’=60゜、
∠BM''M=∠B’MM’=60゜
ゆえに、∠AM''B=120゜
△ABM''の外接円を描く。
線分BCについても同様にして、MをNとして、△BCN''の外接円を描く。
△ABM''の外接円と、△BCN''の外接円の点B以外の交点をP'とする。
線分AP’、線分BP’、線分CP’を引く。
△ABM''の外接円内において、
∠AP’B=∠AM''B=120゜
△BCN''の外接円内において、
∠BP’C=∠BM''C=120゜
ゆえに、
∠AP’C
=360゜−(∠AP’B+∠BP’C)
=360゜−(120゜+120゜)
=120゜
したがって、点P’は求める点Pとなる。(作図終わり)
※三角形の外接円は、二辺の垂直二等分線の交点を中心として描くことができます。
点A,B,Cをドラッグして動かしてみてください。
【紙工作的作図方法】
半透明紙に三角形ABCを描き、それを切り取ります。
別の用紙に円を描きます。中心に印をつけます。
また、半径はそのままで、任意の点から円周上に点1,2,3,4,5,6と番号を付けます。
点1,3,5(点2,4,6でも可)から円の中心に線を引きます。
これを線1,3,5(2,4,6)とします。
先ほどの三角形ABCの紙を用意して、三角形の頂点が、上記の三本の線に乗るように動かします。
(いつかは乗ります)
三角形ABCの紙を透けて現れた、円の中心が求める点Pです。
●感想
計算が複雑になりますが、
「XY座標において、
Y軸、
y=1/![]() x、
x、
y=−1/![]() x
x
の直線(関数)上に、点ABCの座標」
からも考えられます。
これなら求める点Pは、原点Oが答えです。
用紙に正三角形を書いていて、この方法を思いつきました。
◆宮城県 アンパンマン さんからの解答。
まず、Aと同じ側に正三角形A1BCを作ります。
正三角形A1BCの外接円のセンターをO1とします。
BCの垂直二等分線と△A1BCの外接円の交差点をA2 (Aの反対側(BCで))。
A2がセンターになる円A2Bを書きます。
BCの垂直二等分線と円A2Bの交差点をA3。(Aの反対側)。
同じように点B3を作ります。
AA3とBB3の交差点は求める点Pとなります。
点A,B,Cをドラッグして動かしてみてください。
◆大阪府 大野 泰生 さんからの解答。
三角形ABCの外側に以下のふたつの正三角形を作図する。
一辺がABである正三角形ABD
一辺がBCである正三角形BCE
この二つの正三角形の重心を作図しそれぞれをF,Gとする。
Fを中心として半径FA(=FB)の弧ABを書く。
Gを中心として半径GB(=GC)の弧BCを書く。
この交点が、件の点Pである。
理由。書いた二つの弧はいずれも中心角240度の弧ゆえ、
円周角は120度に保たれる。したがって、
角APB=角BPC=120度が保証されている。
よって角CPAも120度。
点A,B,Cをドラッグして動かしてみてください。
◆静岡県 ヨッシー さんからのコメント。
これは、最短シュタイナー問題に関する問題ですが、
三角形の1つの角が120°以上になると、存在しません。
存在する範囲内では、大野泰生さんの方法が一番スッキリしていると思います。
◆東京都 浜田 明巳 さんからの解答。
ABを対角線とし,
1辺の長さがAB/![]() である菱形AO1BDを作図する.
である菱形AO1BDを作図する.
ただしO1は,直線ABに対し,Cと反対側にとる.
具体的には,ABを辺,A,Bを頂点として30°を4個作図し,
交点をD,O1とすればよい.
このとき,∠ADB=120°となる.
次に,O1を中心,半径O1Aの円を作図する.
すると,ABに対して,Dと同じ側にある弧AB上の任意の点をPとすると,円周角の性質から
∠APB=∠ADB=120°
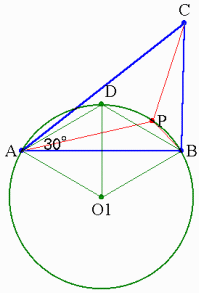
同様に辺BCに対しても円O2を作図する.
2円O1,O2の交点のうち,B以外の点が求める点Pである.
なぜなら,このとき∠CPA=120°となることが明らかだからである.
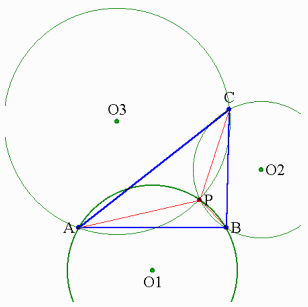
しかし,内角の1つが120°になった場合,このような点は存在しなくなる.
極限として考えられるのは,120°の内角の頂点をPとすることだろう.
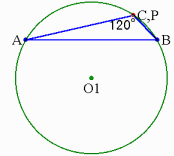
さらに,内角の1つが120°をこえる場合,このような点は存在しない.
このことがらをチェックするVisual Basic(melt.exe 自己解凍)のプログラムを作ってみた.
急いで作成したものなので,荒削りなものではあるが,
内角が120°前後の場合の様子が分かり,それなりに価値のあるもののはずである.
◆林 克巳 さんからの解答。
図のように点Pを通り、どの2直線も60度をなすように三本の直線を引きます。
それぞれの直線上に点A,B,Cをとり三角形ABCの内部に点Pがくるようにします。
点Pは三角形ABCの第6心になります。
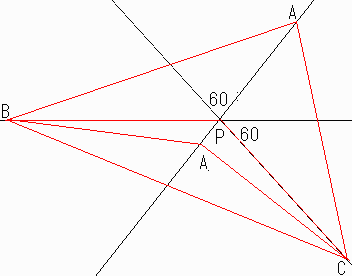
点B,Cは固定し、点Aをその直線に沿って点Pに向かって移動させます。
それにしたがって三角形ABCも移動します。
点Aと点Pが一致したとき三角形の角Aは120度になります。
更に点Pを通過して移動すると角Aは120度を越えます。
この三角形ABCの第6心をこの点Pとするのがよいでしょう。
そこで問題を次のように修正するのがよいでしょう。
「三角形ABCと1点Pをとり、その点Pと各頂点を通る直線(線分でない)を引いたとき、任意の2直線が全て角60度(あるいは全て120度でもよい)をなす。
ただし一つの頂点が120度のときは点Pはその頂点に一致する。」
このようにすればどんな三角形でもただ一つの点Pが定まります。
これを「角心」と呼ぶのはどうでしょうか。
◆神奈川県 いわし さんからのコメント。
林さんのおっしゃる点は、一般には2個あって、それぞれ第1、第2フェルマー点と呼ばれています。
http://mathworld.wolfram.com/FermatPoints.html
を参照してください。
(正三角形なら無限個!)