◆宮城県 甘泉法師 さんからの解答。
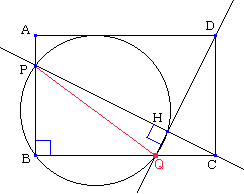
点Bをxy座標の原点に、BCをx軸に、BCをy軸にとる。
∠BCP=αにとる。
【問題1】
直線DHの式はy-2=cotα(x-3)でy切片は2-3cotα。
これと点pのy座標を足して2で割れば線分PHの垂直2等分線のy切片がわかり、
| 式はy=cotαx+ | 2-3cotα+3tanα 2 | 。 |
これと辺PBの垂直2等分線y=3/2 tanαの交点が円の中心であり、
| 座標は( | 3 2 | - tanα, | 3 2 | tanα)。 |
よって
| S π |
= | 9 4 | + | 13 4 | tan2α - 3tanα |
| = | 13 4 | (tanα - | 6 13 | ) | 2 | + | 81 52 |
最小値を与えるαは
| α = arctan ( | 6 13 | )< arctan ( | 2 3 | )、 |
| Sの最小値は | 81 52 | π。 |
【問題2】
点Pをとおり直線DHと平行な直線は
y-2= cotα(x-3+2cotα)、y切片は 2-3cotα+2cot2α。
これと直線DHのy切片2-3cotαを足して2で割れば線分PHの垂直2等分線のy切片がわかり、式は
(1) y=cotαx+2-3cotα+cot2α。
線分BPの中点は(3/2-cotα, 1 )なので線分BPの垂直2等分線の式は
| y-1=- | ( | 3 2 | -cotα | )( | x- | 3 2 |
+cotα | ) |
| (2) y=- | ( | 3 2 | -cotα | ) | x+ | ( | 3 2 |
-cotα | ) | 2 | + 1 |
円の中心である(1)と(2)の交点は
| ( | 5 6 | ,cot | 2 | α- | 13 6 |
cotα+2 | ) | = | ( | 5 6 | , | ( | cotα- | 13 12 | ) | 2 | + | 119 144 | ) |
よってSの最小値を与えるαは
| α = arctan ( | 12 13 | )> arctan ( | 2 3 | )、 |
Sの最小値は
| { ( | 5 6 | ) | 2 | + ( | 119 144 | ) | 2 | } π = | 28561 20736 | π |
◆macsyma2e さんからの解答。
簡単の為、角とその大きさ、線分とその長さの各記号を混用します.
【問題1】
∠CDH = t とすると、∠PCB = t、
| ∠CPB = | π 2 | - t、CH = 2×sin(t)、 |
△CBH に余弦定理を用いて、
BH2 = 9 + 4×(sin(t))2 - 12×sin(t)×cos(t) です.
| よって、△BHP に正弦定理を用いれば、4× | S π |
は |
BH2
|
| =13×x2 - 12×x + 9 |
| =13× | ( | x - | 6 13 | ) | 2 | + | 81 13 |
です.ここで、x = tan(t) であり、
| 6 13 | が定義域 0<x< | 2 3 | に属するので、 |
| Min.( S ) = π× | 81 52 | . |
【問題2】
| ∠DCH = t とすると、∠PCB = | π 2 | - t、 |
△CBH に余弦定理を用いて、
BH2 = 9 + 4×(cos(t))2 - 12×sin(t)×cos(t)、
△ABP に三平方定理を用いて、
BP2 = 13 - 12×tan(t) + 4×(tan(t))2 です.
更に、∠BPH = u とすると、
| BP×sin(u) = 3×sin | ( | π 2 | - t | ) | であることに注意して、 |
| △BHP に正弦定理を用いれば、4× | S π |
は |
| BH2 (sin(u))2 |
| = | BH2 × BP2 ( 3×cos(t) )2 |
| = ( 4×x2 - 12×x + 13 )× | 9×x2 - 12×x + 13 9 |
( 12×x - 13 )×( 6×x2 - 13×x + 12 )
と同符号ゆえ、| 定義域 0<x< | 3 2 | に対して、Min.( S ) = π× | 28561 20736 | . |
【ひとこと】
工夫のない解答になってしまいました.◆宮城県 アンパンマン さんからの解答。
【問題1】
DHとBCの交点をFとします。
| 円の面積= | πPF2 4 | で、PF2の比例になるため、 |
| HC=y、PC=xとするとCF= | xy 3 | ,BF= | 9-xy 3 |
PB=√(x2-9)がわかり、
PF2
=PB2+BF2
| =x2-9+ | (9-xy)2 9 |
| DF2= | ( | xy 3 | ) | 2 | +4, | ( | CF HC | ) | 2 | = | ( | DF DC | ) | 2 | のため、 |
| ( | xy 6 | ) | 2 | +1= | x2 9 |
| つまり y2= | 4(x2-9) x2 | です。 |
| y2= | 4(x2-9) x2 | をPF2の式に代入すると |
9PF2
=13(x2-9)-36√(x2-9)-36+13*9
| =13(√(x2-9)- | 18 13 | ) | 2 | +81- | 324 13 |
最小値のとき、
| √(x2-9)= | 18 13 | でPF2= | 81 13 |
| つまり S= | 81 52 | π |
◆山梨県 Footmark さんからの解答。
【問題1】
動点Pの定義より、Hは長方形ABCDの辺を含まない内部にあり、直線DHは辺BCと必ず交わります。
そこで交点をQとすると、四角形PBQHの対角の和はπになります。
よって、Qも△PBHの外接円の円周上にあり、PQは円の直径に当たります。
△QHCは、△PBCとも△QCDとも相似ですから、△PBCと△QCDも相似です。

| ∴ PB=X とすると QC= | 2 3 | *X |
| ∴ BQ=3- | 2 3 | *X |
| (2R)2=X2+ | (3- | 2 3 | *X | ) | 2 |
| これを解くと、x= | 18 13 | の時、R2の最小値 | 81 52 | を得ます。 |
| よって求める円の最小面積は、 | 81 52 | π となります。 |
【問題2】
図のように、Bより直線PCに下ろした垂線の交点をQとし、3点B,P,Hより得られる円の半径をRとすると、正弦定理より、
| BH sin(∠BPH) | = | BH・BP BQ | =2R |
| ∴ R2= | (BP)2(BH)2 4(BQ)2 |
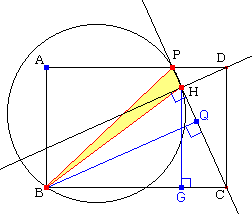
PD=X とすると、ピタゴラスの定理より
(BP)2
=(AP)2+(AB)2
=(3ーX)2+4
=X2ー6X+13
Hより辺BCに下ろした垂線の交点をGとすると、
△PDCと△DHCと△CGHは互いに相似なので、
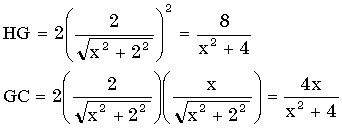
よって、ピタゴラスの定理より
(BH)2
=(HG)2+(BG)2
=(HG)2+{3-(GC)}2
| =( | 8 X2+4 |
) | 2 | +(3- | 4X X2+4 |
) | 2 |
| = | 9X2-24X+52 X2+4 |
また、△CQBも△PDCと相似なので
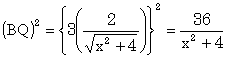
∴R2
| = | (BP)2(BH)2 4(BQ)2 |
| = | (X2-6X+13)(9X2-24X+52) 144 |
| = | 9X4-78X3+313X2-624X+676 144 |
| = | (3X2-13X+24)2+100 144 |
上式より、R2 の最小値は明らかに
| X= | 13 3 |
/2= | 13 6 |
の時だと分かるので、代入すると |
| R2= | {( | 119 12 | ) | 2 | +100}/144= | 28561 20736 |
| Xが | 13 6 |
の時、APは 3- | 13 6 |
= | 5 6 |
なので、 |
| APが | 5 6 |
の時に円の面積は最小の | 28561 20736 |
π となります。 |
[ 補足 ]
図の線分PC上でHとQの位置が逆になっても、示した計算には何ら支障はありません。
| X= | 13 6 |
を (BP)2 の式に代入すると、BP= | 13 6 |
を得ます。 |
【問題1】の場合は、直線PQが直線ACと平行になった時、円の面積は最小になります.
この関係は、むしろ【問題1】の方が気付きにくいと思います。