仧峀搰導丂惔愳丂堢抝丂偝傫偐傜偺夝摎丅
倶亅倷嵗昗偱壖偵侾偺栘傪尨揰偵庢傝丄媮傔傞揰傪媮傔傑偟偨丅
搑拞偺寁嶼偼徣棯偟偰丄寢榑偲偟偰傢偐偭偨偙偲偼埲壓偺捠傝偱偡丅
俀偺栘偲俁偺栘傪寢傃丄偦偺慄暘偑懳妏慄偲側傞惓曽宍傪嶌傝丄栘偺側偄擇偮偺捀揰偑丄曮偺偁傞岓曗揰偲側傞丅
侾偺栘偑傢偐傜側偄偺偱丄嵍塃偼憡懳揑偲側傞偺偱丄岓曗揰偼侾揰偵峣傟側偄丅
摉慠偺偙偲偱偡偑岓曗揰偲俀偺栘丄俁偺栘傪寢傫偱偱偒傞嶰妏宍偼丄捈妏擇摍曈嶰妏宍偱偡丅
埲忋偱偡丅
嵗昗忋偱峫偊傞偺偼丄曋棙偱偡偹丅惓夝偱偁傟偽偺偙偲偱偡偑丅
仧惷壀導丂儓僢僔乕丂偝傫偐傜偺夝摎丅
俀偺栘偺嵗昗傪(侽丆侽)丄
俁偺栘偺嵗昗傪(俀倎丆侽) (倎亞侽)偲偟丄
侾偺栘偺嵗昗傪(倶丆倷)丂偲偟傑偡丅
乽侾偐傜俀偵岦偐偭偰曕悢傪悢偊側偑傜曕偗丅
俀偺栘偵偮偄偨傜塃傊俋侽亱岦偒傪曄偊丄峏偵摨偠曕悢偩偗曕偗丅乿
偵傛偭偰丄峴偒拝偄偨揰偼丄
(倶丆倷)傪尨揰廃傝偵俋侽搙夞揮偟偨揰側偺偱丄
丂(亅倷丆倶)
乽侾偐傜俁偵岦偐偭偰曕悢傪悢偊側偑傜曕偗丅
俁偺栘偵偮偄偨傜嵍傊俋侽亱岦偒傪曄偊丄峏偵摨偠曕悢偩偗曕偗丅乿
偵傛偭偰丄峴偒拝偄偨揰偼
(倶丆倷)傪丄倶曽岦偵亅俀倎堏摦偟丄
尨揰廃傝偵亅俋侽搙夞揮偟丄
倶曽岦偵俀倎堏摦偟偨揰偱偁傞偐傜丄
(倶丆倷)仺(倶亅俀倎丆倷)仺(倷丆俀倎亅倶)仺(倷亄俀倎丆俀倎亅倶)丂偙偺俀揰偺拞揰偼
丂乷(亅倷丆倶)亄(倷亄俀倎丆俀倎亅倶)乸亊侽丏俆
亖(倎丆倎)
傛偭偰丄曮偺埵抲偼丄侾偺栘偺埵抲偵娭學側偔堦掕偲側傞丅
摎偊
乽俀偲俁偺拞娫揰偵朹傪棫偰傛丅
俀偐傜朹偵岦偐偭偰曕悢傪悢偊側偑傜曕偗丅
朹偵偮偄偨傜嵍傊俋侽亱岦偒傪曄偊丄峏偵摨偠曕悢偩偗曕偗丅
偦偙偵曮偑杽傑偭偰偄傞丅乿
亂僐儊儞僩亃
丂俀偲俁偺栘傪寢傇捈慄傪幬曈偵帩偮捈妏擇摍曈嶰妏宍偺捈妏偺妏偺捀揰偲偄偆偙偲偱偡偹丅
弌戣幰偺崅峑惗偺曽偵傛傞偲丄偙偺栤戣傪拞妛惗偺屻攜偵夝偄偰傕傜偭偨偲偙傠丄弶摍婔壗偱夝偄偨偦偆偱偡丅
傑偨丄堦弿偵偙偺栤戣傪嶌偭偨桭恖偼婳愓傪梡偄偰夝偄偨偦偆偱偡丅
戝擔杮恾彂 偝傫偺偛岤堄偱丄幚嵺偵幚尡偱偒傞傛偆偵側傝傑偟偨丅
侾偺傕傒偺栘偑摦偄偰傕丄曮偺埵抲偑堦掕偱偁傞偙偲偑暘偐傞偲巚偄傑偡丅
仧垽抦導偺崅峑惗丂傂傠丂偝傫偐傜偺夝摎丅
倃倄暯柺偵偍偄偰丄(2)偺栘傪尨揰偵偲傝丄(3)偺栘傊傑偭偡偖倃幉傪偲傞丅
偙偺帪(3)偺栘傪丂(3)乮俙丆侽乯丂偲偡傞丅
壖偵(1)偺栘傪丂(1)乮倃丆倄乯偲偍偔偲
(2)偺栘偺僋僀丂嘦丂偼嘦乮亅倄丆倃乯
(3)偺僋僀丂嘨丂偼嘨乮俙亄倄丆俙亅倃乯
乮佹嶰妏宍偺崌摨傛傝乯
傛偭偰嘦偲嘨偺僋僀偺拞揰偼丂(1)乮倃丆倄乯偵娭傢傜偢
| 曮乮 | 俙 俀 | 丆 | 俙 俀 | 乯偲側傞丅 |
丂丂丂曮 丂丂丂丒 丂丂丂丒 丂丂丂丒 (2)丒丒丒丒丒丒丒(3)
仧搶嫗搒丂朠丂墱恖丂偝傫偐傜偺夝摎丅
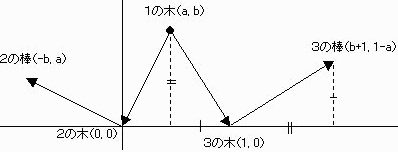
俁杮偺栘偺埵抲傪嵗昗偱昞偟偰傒傑偡丅
侾偺栘傪乮倎丆倐乯
俀偺栘傪乮侽丆侽乯
俁偺栘傪乮侾丆侽乯丂偲偟傑偡丅
俀偺栘傪婎弨偵偟偨朹偺埵抲偼乮亅倐丆倎乯
俁偺栘傪婎弨偵偟偨朹偺埵抲偼乮倐亄侾丆侾亅倎乯
| 偦偺拞揰偼乮 | 侾 俀 | 丆 | 侾 俀 | 乯丅 |
偮傑傝倎傗倐偺抣偵傛傜偢堦掕両
偙偺嵗昗偐傜敾抐偱偒傞丄幚嵺偵栚揑偺応強傊偨偳傝偮偔曽朄偼
乽俀偺栘偐傜丄俀偺栘偲俁偺栘偺拞揰傑偱曕悢傪悢偊偰曕偒丄拞揰傑偱偨偳傝偮偄偨傜俋侽搙嵍傊嬋偑傝丄摨偠曕悢偩偗曕偔乿
偲偄偆偙偲偵側傞丄偲巚偄傑偡丅
恾偼侾偺栘偺攝抲応強偺堦椺偱偡偑丄懠偺偳偺応強偵偁偭偰傕俀杮偺朹偺嵗昗偺彂偒曽偼忋偺捠傝偵側傞偼偢偱偡丅

嵗昗暯柺傪梡偄偢丄晛捠偺恾宍栤戣偲偟偰夝偗偲尵傢傟偨傜丒丒丒偪傚偭偲偍庤忋偘偱偡丅