『３つの半円Part２』解答

◆広島県　清川　育男さんからの解答。

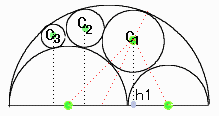
３つの半円の半径をa，b，c
a>b>cとする。a=b+c
C₁から半円への垂線と半円との交点を、h1とする。

Part1のときと、同じ解法を使う。円C₁の半径をxする。
ヘロンの公式を用いる。

S＝1/2((b+x)+(a-x)+c)=1/2(a+b+c)
a=b+c　よってs=a

1/2((c+x)+(a-x)+b)=1/2(a+b+c)=a=s

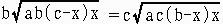
これを整理すると、
a(b-c)x((b²+bc+c²)x-bc(b+c))=0
b-c≠0，　x≠0,よって

x=(bc(b+c))/(b²+bc+c²)
b+c=a
よって、x=abc/(b²+bc+c²)

ch1をyとする。三平方の定理により、

(c+abc/(b²+bc+c²))²-y²+(a-y)²=(b+abc/(b²+bc+c²))²

y=(c²(2b+c))/(b²+bc+c²)

求める c1h1は、

(c+abc/(b²+bc+c²))²-((c²(2b+c)/(b²+bc+c²))²

=(2bc(b+c)/(b²+bc+c²))²
=(2abc/(b²+bc+c²))²

よって、c1h1=2abc/(b²+bc+c²)

c1h1=2x
c1h1は円c1の直径に等しい。

【感想】

とりあえずここまでとします。ああ疲れた。
半ば、この方法での限界を感じました。
がんばって、みるつもりですが。

【コメント】

　たしかにこの方法で、次のレベルまでいくのはつらそうですね。
なにか発想の転換が必要になりそうです。

◆静岡県　ヨッシー さんからの解答。

大きい半円の半径をａ、左側の小さい半円の半径をｂとすると、右側の小さい半円の半径はａ−ｂとなります。

大きい半円の中心をＯ（０，０）とし、直径方向をｘ軸とします（右が正）。
このとき、左右の小さい半円の中心は
それぞれ、Ａ（ｂ−ａ，０）、Ｂ（ｂ，０）となります。

この３つの半円に接する円（Ｃ₁）の中心の座標をＰ（ｘ、ｙ）、半径をｒとします。
また、Ｐからｘ軸におろした垂線の足をＱ（ｘ，０）とします。

△ＯＰＱ、△ＡＰＱ、△ＢＰＱにおける三平方の定理より、

　（ａ−ｒ）²＝ｘ²＋ｙ²
　（ｂ＋ｒ）²＝（ｘ＋ａ−ｂ）²＋ｙ²
　（ａ−ｂ＋ｒ）²＝（ｘ−ｂ）²＋ｙ²

この３つの連立方程式を解くと、

ｒ＝	ａｂ(ａ−ｂ) ――――――――― ａ2−ａｂ＋ｂ2

ｘ＝	ａ2(２ｂ−ａ) ――――――――― ａ2−ａｂ＋ｂ2

ｙ＝

２ａｂ(ａ−ｂ) ――――――――― ａ2−ａｂ＋ｂ2

・・・【１】

となります。

　一方、自然数ｎについて、
大きい半円と、左の小さい半円に接する円で、中心のｙ座標が直径のｎ倍である円を考えます。

半径をｒ_n、中心をＰ_n（ｘ_n、ｙ_n）とすると、ｙ_n＝２ｎｒ_n とおけます。

また、Ｑ_n（ｘ_n、０）とします。
△ＯＰ_nＱ_n、△ＡＰ_nＱ_n における三平方の定理より、
　（ａ−ｒ_n）²＝ｘ_n²＋４ｎ²ｒ_n²
　（ｂ＋ｒ_n）²＝（ｘ_n＋ａ−ｂ）²＋４ｎ²ｒ_n²

これを解いて、

ｒn＝	ａｂ(ａ−ｂ) ―――――――――― ａｂ＋ｎ2(ａ−ｂ)2

ｘn＝

ａｂ(ａ＋ｂ) ―――――――――― ａｂ＋ｎ2(ａ−ｂ)2

−ａ

ｙn＝

２ｎａｂ(ａ−ｂ) ―――――――――― ａｂ＋ｎ2(ａ−ｂ)2

・・・【２】

【２】で表される円群をＣｎ（ｎは自然数）とします。

（ｘ_k−ｘ_k+1）²＋（ｙ_k−ｙ_k+1）²−（ｒ_k＋ｒ_k+1）²＝０
（途中計算省略）

より、Ｃ_k と Ｃ_k+1 は、中心距離が半径の和に等しいので外接します。

さらに、ｘ_n はｎに伴い単調減少することと、ｎ＝１とすると、【２】は【１】に一致することから、円群Ｃn は、問題に示されたように、次々に接していく。

【コメント】

　大変すっきりした証明で、すばらしいです。
実はこの問題はかなりテクニカルな証明が有名なのですが（ひまを見て掲載します）、個人的にはヨッシーさんの証明に賛同したいと思います。

　『３つの半円Part２』へ

　数学の部屋へもどる